由于磁芯由铁磁材料制成,因此许多磁芯都具有导电性。当暴露于交流磁场时,这些磁芯会产生称为涡流的小电流环。在
变压器中,涡流可能是造成功率损耗的重要原因。
特别是在低频下,减少涡流损耗的常用方法是使用由薄
磁性材料片制成的磁芯。这些薄片称为叠片,厚度通常只有几分之一毫米,彼此之间通过一层薄氧化物绝缘。在本文中,我们将了解不同参数如何影响叠片磁芯中的涡流损耗。为了简单起见,我们将讨论范围限制在低频操作上。
什么是涡流损耗? 根据法拉第定律,变化的磁场会在导线中感应出电动势,从而产生电流。同样,变化的磁场也会在放置在其中的一大块导电材料中产生循环电流(图 1)。
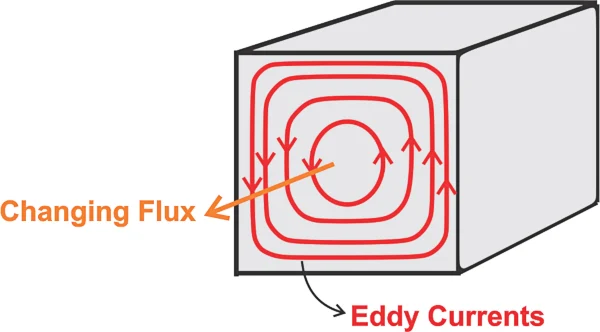
变化的磁场会在一大块导电材料(在本例中为导电芯)中产生环流。
图 1.变化的磁场在导电磁芯中产生涡流。
当涡流流过材料时,它们不可避免地会在路径上遇到一些电阻。这会导致I 2 R能量损失,其中I是电流,R是路径电阻。
要计算结构中的涡流损耗,我们需要知道材料中每条路径的电流和电阻。一旦我们知道所有不同路径的损耗,我们就会将它们相加以得到总涡流损耗。我们很快就会用这种方法推导出叠层铁芯中涡流损耗的公式。
在我们继续之前,值得一提的是,涡流在某些应用中是有益的。例如,电磁制动系统使用涡流来减慢或停止移动物体,如火车和过山车。另一个应用是感应加热,其中涡流用于故意加热金属物体。然而,涡流在
电感器和变压器中是不可取的,因为它们会将能量以热量的形式耗散,并降低设备的效率和性能。
什么是层压铁芯?
对于低频、高功率应用,叠层铁芯是一种经济的降低涡流损耗的方法。图 2 显示了叠层铁芯中的涡流流动方式。
叠片铁芯中的涡流流动。
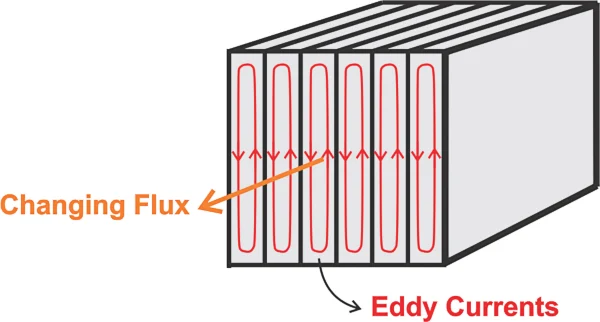
图 2.叠层铁芯中的涡流。
请注意,叠片与磁通平行,而涡流则垂直。这种布置将涡流限制在叠片的宽度内。如图 3 所示,叠片与磁通垂直的叠层铁芯对减少涡流损耗几乎没有作用。
层压结构垂直于磁通的铁芯中的涡流与非层压铁芯中的涡流看起来相同。
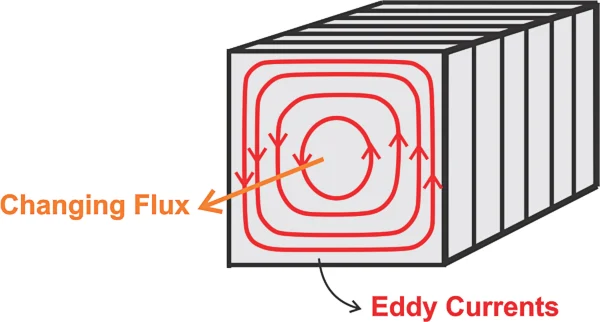
图 3.垂直于磁通的层压板对于减少涡流损耗不是很有效。
为了更好地理解叠层铁芯中的涡流损耗,让我们从数学角度对其进行分析。对于那些对数学细节不太感兴趣的人,在研究了初步分析的关键要点之后,我们还将对数学铁芯进行更简单的解释。
了解低频叠层铁芯中的涡流损耗
考虑厚度为t、高度为h、深度为l 的层压板,如图 4 所示。终的铁芯是由许多这样的层压板堆叠而成的。
单芯层压板的横截面图。

图 4.单个层压板的横截面图。
外部施加的磁场均匀且垂直于层压板的正面。对于足够低的工作频率,我们可以假设趋肤深度远大于层压板的厚度(δ?t )。因此,磁通密度分布在层压板的横截面上将是均匀的。
图中的灰色区域显示了涡流的可能路径。让我们检查一下流经该路径的电流,该路径距离正面中心线为x ,宽度为dx。该路径的面积为:
A = 2x × h
等式 1.
假设材料中的磁通密度是正弦的:
B = Bmsin(ωt)
等式 2.
在哪里:
B m是磁通密度的峰值
ω 是角频率
t是时间(不是厚度!)。
因此,通过灰色路径的磁通量为:
Φ = A × B = 2xhBmsin(ωt)
等式 3.
当封闭区域内的磁通量随时间变化时,它会产生电动势 (EMF),可以使用法拉第定律计算:
v = NdΦdt = 2xhBmωcos(ωt)
等式 4.
在我们的例子中,法拉第公式中的匝数为N = 1。因此,感应电压的峰值为:
Vm = 2xhBmω
等式 5.
正如预期的那样,感应电压与x成正比。这是因为距离中心线较远的路径对应的封闭面积较大,因此磁通量的变化也较大。
现在我们可以计算电流路径的电阻了。由于层压板的高度远大于其厚度,因此总电阻约等于图中AB和CD路径电阻的总和。计算导体电阻的常用公式是:
R = ρlA
等式 6.
在哪里:
ρ 是导体的电阻率,单位为 Ω·m
l是导体的长度(以米为单位)
A为其横截面积(单位为平方米)。
如果我们回顾图 4,AB和CD路径具有相同的参数。因此,每个路径的电阻等于:
RAB = RCD = ρhldx
等式 7.
因此,灰色电流路径中耗散的涡流功率为:
dPe = Vm22Rtotal = (2xhBmω)2l4ρhdx= (Bmω)2lhρx2dx
等式 8.
层压板中耗散的总涡流功率可以通过将上述方程在x = 0 至x = t /2 范围内积分来得出,其中t为层压板厚度:
Pe = ∫t/20dPe = (Bmω)2lhρ∫t/20x2dx = (Bm)2ω2lht324ρ
,注意到(l × h × t)实际上是层压板的体积,我们可以确定功率损耗的密度:
pe = (Bm)2ω2t224ρ
等式 10。
重要观察
公式 10 显示了不同参数如何影响叠层铁芯中的涡流损耗:
频率 (ω):涡流损耗与频率的平方成正比。这与磁滞损耗相反,磁滞损耗随频率线性增加。
叠片厚度 ( t ):涡流损耗与叠片厚度的平方成正比。为了地减少铁芯损耗,叠片应尽可能薄。
电阻率(?):为了减少涡流损耗,使用电阻率高的材料,例如硅钢。
在高频下,我们通过使用铁氧体磁芯而不是层压铁芯来减少涡流损耗。铁氧体是由氧化铁和其他金属氧化物制成的陶瓷型材料。它们的电导率非常低——约为 1 S/m,是铁的百万分之一。因此,铁氧体中的涡流损耗通常很容易控制。
叠层铁芯的直观解释
涡流会产生欧姆功率损耗。损耗取决于磁芯中感应出的 EMF 量和磁芯的电阻。对于连接到峰值电压为V m的正弦电压的电阻 ( R ) ,耗散功率为:
P = Vm22R
等式 11.
当我们用具有n 个叠层的叠层铁芯替换实心铁芯时,每个叠层的横截面积为实心铁芯的
。这意味着每个叠层中的感应 EMF ( V L ) 是实心铁芯中的
VLVS = 1n
此外,每个层压板的电阻(R L)是实心磁芯电阻(R S)的n倍:
RL = nRS
等式 13.
令P S和P L分别为实心磁芯的耗散功率和单层铁芯的耗散功率。根据公式 11,我们可得出:
PLPS = (VLVS)2 × RSRL = 1n3
等式 14.
由于总共有n 个叠片,叠片铁芯中耗散的总功率是实心铁芯的
。请注意,此结果与公式 10 一致。它们都表明,当我们将叠片厚度减小n倍(或者,等效地,将叠片数量增加n倍)时,涡流损耗会减少。
示例问题:计算新的涡流损耗
层压厚度为t 1 = 0.5 mm的磁芯在频率 f 1 = 50 Hz下运行时,涡流损耗为p 1 = 50 W/m 3。如果我们将工作频率提高到f 2 = 250 Hz,并使用厚度为t 2 = 1 mm 的层压板,新的涡流损耗是多少?假设磁通密度和电阻率保持不变。
从公式 10 可知:
p2p1 = (f2f1)2 × (t2t1)2
等式 15.
代入示例开始时给出的值,我们得到:
p250 = (25050)2 × (10.5)2 ? p2 = 5000 W/m3" role="presentation" style="box-sizing: inherit; border: 0px; display: inline-block; line-height: 0; font-size: 18.08px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; margin: 0px; padding: 1px 0px; position: relative;">p250 = (25050)2 × (10.5)2 ? p2 = 5000 W/m3
由于频率和层压厚度的增加,涡流损耗从50W/m3增加到5,000W / m3。



