卡诺图化简法是一种用于化简逻辑函数的直观方法,尤其适用于变量较少(通常不超过六个)的情况。下面我将提供一个卡诺图化简法的例题详解,以帮助理解其原理和应用步骤。
例题
给定一个逻辑函数的真值表如下:入变量,L为输出变量。
卡诺图化简法步骤
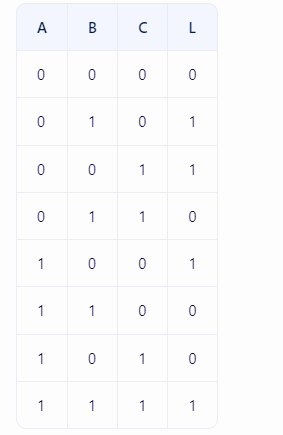
构造卡诺图:根据输入变量数量(本例为3个),绘制一个3变量的卡诺图。卡诺图的每个方格代表一个项,方格中的数字是该项的编号(通常是基于二进制编码的十进制表示)。
填充卡诺图:根据真值表,在卡诺图中对应的方格内填入“1”(表示L为真的情况),其余方格填入“0”。
画包围圈:在卡诺图中找相邻的“1”方格,并用包围圈(可以是矩形或椭圆形)圈起来。相邻方格是指只有一个变量取值不同的方格。合并的原则是尽可能使包围圈大,以消去更多的变量。
对于本例,可能的包围圈如下:
包围圈1:包含方格2(B'C')、方格3(BC')和方格5(A'B'C),可以消去变量C。
包围圈2:包含方格4(B'C)和方格6(A'B'C'),可以消去变量B。
包围圈3(可选):包含方格1(A'B'C')和方格8(ABC),但这样并不能消去任何变量,所以这个包围圈不是必须的。
写出简表达式:根据包围圈,写出每个包围圈对应的简与项(取值为1的变量用原变量表示,取值为0的变量用反变量表示),然后将所有与项进行逻辑加(OR运算)。
对于本例,简表达式为:
(L = (B' + C')(A'B' + C) + A'B'C')
注意:由于卡诺图化简法是基于直观的几何操作,因此得到的简表达式可能不是的。另外,当变量数量较多时,卡诺图会变得复杂,此时可能需要采用其他方法(如代数法)来化简逻辑函数。
