之前,我们了解了
MOSFET 共源
放大器的大信号和小信号行为。这些分析虽然有用,但仅适用于低频操作。为了了解共源 (CS) 放大器如何在较高频率下工作,我们需要更详细地检查其频率响应。
在本文中,我们将推导出考虑 MOSFET 寄生电容的 CS 放大器的完整传递函数。不过,在此之前,让我们花点时间更全面地回顾一下频域中的传递函数 (TF) 分析。
s 域传递函数 TF 是一个方程,表示线性系统如何操纵输入信号 ( x ) 来产生输出信号 ( y )。它的形式如下: H(s) = A(s ? Z1)(s ? Z2)....(s ? Zn)(s ? P1)(s ? P2)....(s ? Pm)
等式 1。
在哪里: s指复数频率,定义为 ( s = σ + jω)。
Z 1 .... Z n指的是传递函数的所有零点。
P 1 .... P m指传递函数的所有极点。
零是导致传递函数的分子等于零的s值。极点是使传递函数的分母为零的s值。
波特图 波特图是我们分析传递函数强大的工具之一。伯德图由 TF 在一定频率范围内的幅度和相位测量值组成。它告诉我们系统有什么样的响应(低通、高通、带阻等),并指示 TF 中任何极点和零点的位置。
极点和零点对系统的幅度和相位响应有不同的影响。这些总结如下:
幅度响应: 在极点频率处,TF 的斜率变化为 –20 dB/十倍频程。
在零频率处,TF 的斜率变化为 +20 dB/十倍频程。
相位响应:
–90 度相移从极点前十年开始,到极点后十年结束。
+90 度相移从复空间左侧平面中的零值前一个十年开始,并在十年后结束。
可以看到 –90 度相移从复空间右侧平面中的零值前 10 年开始,到 10 年后结束。
图 1 显示了带通滤波器的波特图,该滤波器在 1 rad/s 处具有单极点,在 1000 rad/s 处具有单零点。
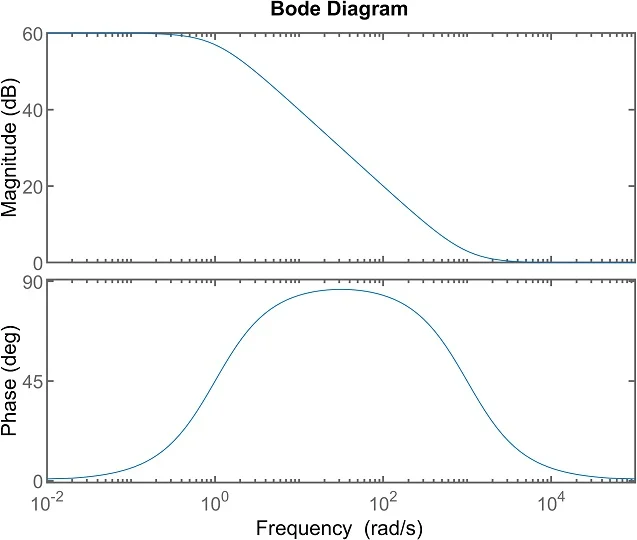
Hs = s ? 1000s ? 1
带通滤波器的波特图,极点为 1 rad/s,零点为 1000 rad/s。
图 1.传递函数的伯德图:
有关 s 域传递函数的更多信息,我推荐 Robert Keim 撰写的技术文章“了解低通滤波器传递函数”。
共源放大器的基本频率响应
在我们之前的一篇文章中,我们讨论了 MOSFET 中不同类型的寄生电容。现在,我们将把它们合并到具有简单电阻负载的共源放大器中(图 2)。为了获得有意义的结果,我们假设输入电压源具有非零输入电阻 ( RS ),这是任何实际
驱动器的特征。
带寄生电容的CS放大器和放大器的小信号模型。
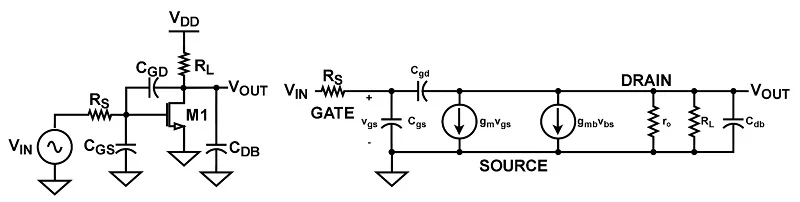
图 2.带有寄生电容的 CS 放大器(左)。放大器的小信号模型(右)。
图 2 的右侧部分显示了该 CS 放大器的小信号模型。看看它,我们已经可以看到这个分析将比以前复杂得多——栅漏电容没有连接到交流接地,这使事情变得复杂。为了简化我们的分析,我们将利用米勒效应。
米勒效应
米勒效应表明,如果阻抗 (Z) 与增益为 A 的反相放大器并联(图 3,左),则它可以在放大器的输入和输出处分成两个独立的阻抗(图 3) , 正确的)。输入和输出阻抗的值为
Zin = Z1 + A 和 Zout = Z1 + 1A
分别,并且都接地。
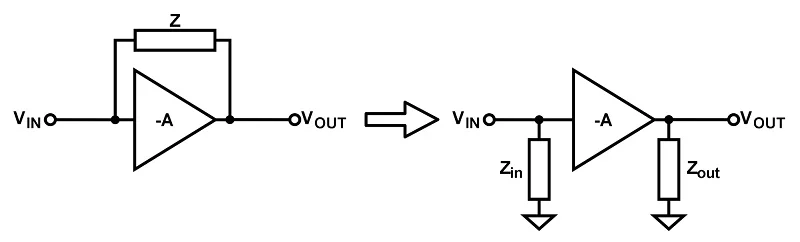
具有并联阻抗的放大器,以及放大器的米勒等效电路模型。
图 3.具有并联阻抗的放大器(左)。放大器的米勒等效电路模型(右)。
如果Z是
电容器,则Z C = 1/ sC 并且输入电容 ( C in ) 因此有效地乘以 (1 + A )。这个新的 C in是米勒电容。
通过使用米勒电容作为C in,我们可以将图 2 中所示的 CS 放大器控制为我们很快就会在图 4 中看到的放大器。现在我们有两个清晰的 RC 电路,一个位于放大器输入端,一个位于输出端。结果,我们有两个极点:
ωin = 1RS(Cgs + Cin)
等式2。
和:ωout = 1(ro||RL)(Cdb + Cout)
等式 3。
给我们一个总传递函数: H(s) = ?gm(ro||RL)(1 + sωin)(1 + sωout)
等式 4。
我们的新型 CS 放大器原理图如图 4 的左半部分所示。该图的右半部分显示了放大器的小信号模型。

具有米勒效应的CS放大器及其小信号等效电路模型。
图 4.具有米勒效应的 CS 放大器(左)。其小信号等效电路模型(右)。
真实频率响应
尽管米勒效应准确地预测了两极 TF,但在某个地方有一个隐藏的零没有被考虑在内。我们在图 5 的频率响应图中看到了这一点 - 在 100 和 1000 GHz 之间,两个 –20 dB/十倍频程斜率之间有一个相对平坦的区域。该零是由于C GD在高频时在放大器的输入和输出之间产生短路所致。

图 2 中 CS 放大器的频率响应。
图 5.图 2 中 CS 放大器的频率响应(RL = 10 kΩ, RS = 100 Ω)。
米勒效应可以为我们提供 CS 放大器传递函数的良好估计,但是(如图 5 所示)该估计并不完全符合放大器的实际行为。C GD会引起更复杂的响应,我们需要创建一个反映这一点的方程。尽管在实际设计中我们不会手动计算传递函数,但注意极点和零点所依赖的电路参数对于确保所需的操作至关重要。
为了计算真实的传递函数,我们将参考图 2 中所示的小信号模型。使用基尔霍夫电压和电流定律,我们得到以下传递函数
等式 5。
公式 5 的分子中的零与我们在图 5 中看到的频率响应相匹配。
关于C GD产生的零的一个有趣的事情是,虽然 CS 放大器通常是反相放大器,但这种短路会导致非反相行为。事实上,它可能会引起正反馈,可能导致放大器不稳定,输出端出现振荡。




