什么是小信号分析?
当我们说“小信号”时,我们到底是什么意思?为了定义这一点,让我们参考图 1,它显示了
逆变器的输出传输特性。
逆变器的传输特性。
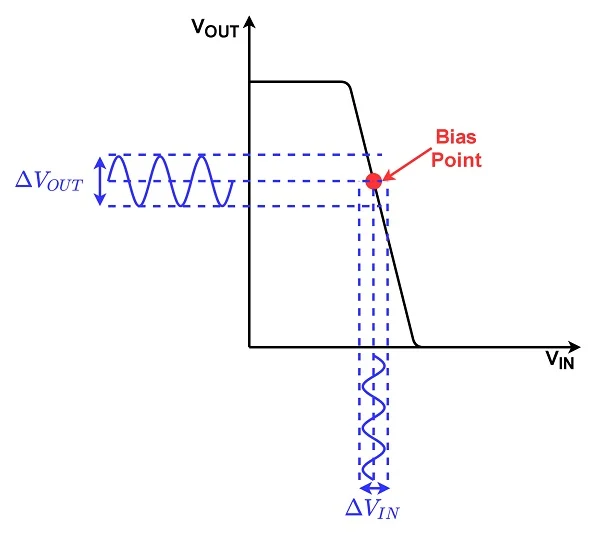
图 1.逆变器的传输特性。
假使,假设:
V IN和V OUT都是直流电压。
V IN的值意味着我们正在偏置点(标记为红色)操作。
在小信号分析中,我们在直流偏置电压之上应用非常小的交流信号 (Δ V IN )。产生的输出交流电压根据偏置点处传输特性的斜率 (– A V ) 进行放大:
$$\Delta V_{OUT}~=~ -A_{V} \times \Delta V_{IN}$$
等式 1。
请注意,由于斜率的方向,A V仅是负值。我们将在本文后面回到AV 。目前,重要的一点是偏置点(大信号行为)会影响输出信号接收的增益量(小信号行为)。
小信号参数
在对电路的行为进行建模之前,我们需要定义参数。MOSFET 的主要小信号参数为:
跨导(g· m)。
输出电阻 ( r o )。
固有增益 ( AV )。
体效应跨导 ( g mb )。
单位增益频率 ( f T )。
除了f T之外(在创建高频 MOSFET 模型之前我们不会讨论它),我们将在接下来的部分中定义并推导上述每个术语。我们首先查看I - V特性、跨导。
跨导
我们已经知道,MOSFET 将输入电压转换为输出电流。小信号输出电流与小信号输入电压之比称为跨导( g m )。我们还可以将跨导视为输出电流与栅源电压的导数。
线性区域的跨导可以定义为:
$$\begin{array}{} g_{m,lin}~=~\frac{\delta I_{D}}{\delta V_{GS}}~=~\frac{\delta \left( \mu C_ {ox} \frac{W}{L} \left[(V_{GS}~-~V_{th})V_{DS}~-~\frac{(V_{DS})^2}{2} \右] \right)}{\delta V_{GS}} \\~=~ \mu C_{ox} \frac{W}{L} V_{DS} \end{array}$$
等式2。
对于饱和区,为:
$$\begin{array}{} g_{m,sat}~=~\frac{\delta I_{D}}{\delta V_{GS}}~=~ \frac{\delta \left[ \frac{ 1}{2} \mu C_{ox} \frac{W}{L} (V_{GS}~-~V_{th})^{2} \right]}{\delta V_{GS}} \\ ~=~ \mu C_{ox} \frac{W}{L} (V_{GS}~-~V_{th}) \end{array}$$
等式 3。
在哪里:
I D是漏极电流
V GS是栅源电压
V DS是漏源电压
V th是阈值电压
μ 是
晶体管迁移率
C ox是栅极氧化层电容
W是晶体管的宽度
L是晶体管的长度。
这两个方程让我们得出一些有趣的观点:
当处于线性区域时,晶体管的电流增益取决于输出电压。它完全不依赖于输入信号。这在实践中并不理想,因为增益在工作范围内会发生巨大变化。
在饱和状态下,跨导仅取决于输入电压。
短而宽的器件可限度地提高给定输入偏置电压的电流增益。
输出电阻
下一个感兴趣的参数是输出电阻( r o )。这被定义为晶体管的漏源电压相对于漏电流的变化。我们可以通过绘制漏极电流与V DS 的关系来找到输出电阻。所得直线的斜率等于r o的倒数。
让我们看一下图 2 中的图。我们在之前有关MOSFET 结构和操作的文章中首次看到该图,它帮助我们比较了 NMOS 和 PMOS 晶体管的漏极电流。
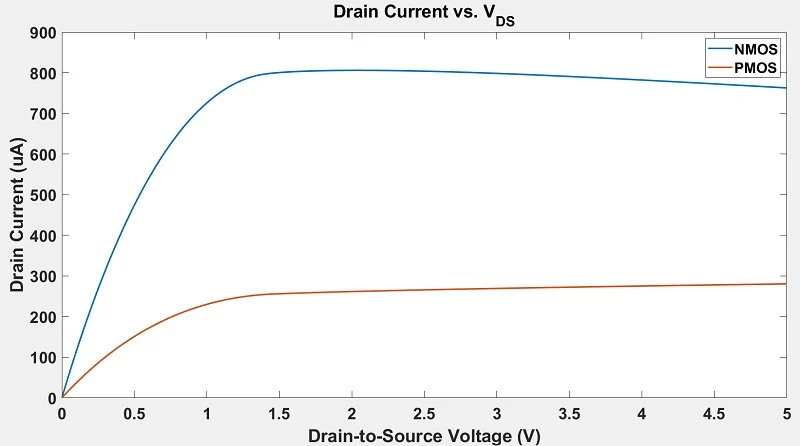
NMOS 和 PMOS 晶体管的漏极电流与漏极至源极电压。
图 2. NMOS 和 PMOS 晶体管的漏极电流与V DS的关系。宽/长=10微米/2微米。
MOSFET在线性区时输出电阻较小,在饱和区时输出电阻较大。在上图中,NMOS 和 PMOS 晶体管均在约 1.5 V 时进入饱和状态。
因为正如我们在跨导中看到的那样,饱和区提供了更好的小信号性能,所以我们只关心晶体管饱和时的输出电阻。我们可以这样计算:
$$\begin{array}{} &r_o ~=~\left( \frac{ \delta I_{D}}{ \delta V_{GS}} \right)^{-1} ~=~& \frac{1 }{ \left( \frac{\delta I_{D}}{\delta V_{GS}}\right)} ~=~ \frac{1}{ \left( \frac{\delta \left[\frac{ 1}{2} \mu C_{ox} \frac{W}{L} \left(V_{GS}~-~V_{th} \right)^{2} \left(1~+~ \lambda V_ {DS} \right) \right]}{\delta V_{DS}} \right) } \\ &~=~\frac{1}{\lambda I_{D}}~ \propto ~ \frac{L^ {2}}{ \left( V_{D,sat} \right)^{2}}& \end{array}$$
等式 4。
其中 λ 是通道长度调制。
当您考虑到饱和状态下 IV 曲线的斜率是由沟道长度调制产生时,r o和 λ之间的关系就有意义了。方程 4 还告诉我们:
r o随着漏极电流 ( I D ) 的增加而减小。
由于上述原因,ro随着过驱动电压 ( V D,sat ) 的增加而减小。
r o随着晶体管长度 ( L ) 的增加而增加。
内在增益
现在我们知道了晶体管的输出电阻和电流增益,我们可以计算它的电压增益。这也称为晶体管的固有增益( AV )。为了更好地理解固有增益的概念,我们来看看图 3 中的共源放大器配置。
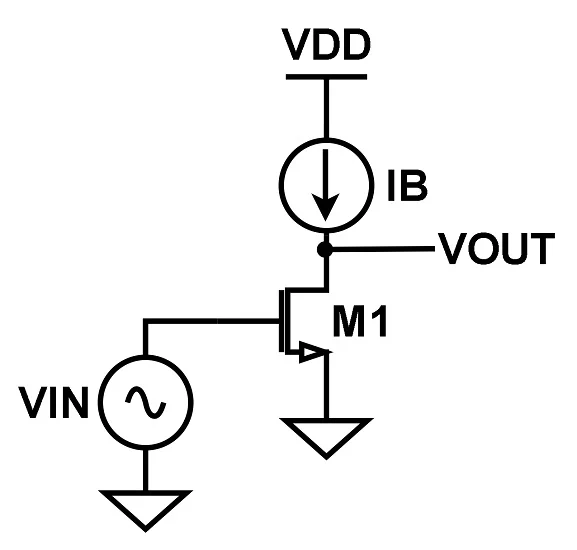
配置为共源放大器的 NMOS 晶体管的电路图。
图 3.配置为共源放大器的 NMOS 晶体管。
由于理想
电流源具有无穷大的电阻,因此该电路的小信号输出传递函数可以计算为:
$$\frac{\delta V_{OUT}}{\delta V_{IN}}~=~\frac{\delta V_{DS}}{\delta V_{GS}}~=~ g_{m} r_{ o}~=~A_{V}$$
等式 5。
从公式 3 和公式 4 可以看出,g m和r o与漏极电流成反比。利用这些知识,我们可以找到漏极电流的值,该值可以为单个晶体管产生的增益,换句话说,就是其固有增益。对于现代工艺,内在增益通常在 5 到 10 之间。
体效应跨导
我们需要导出的一个小信号参数是体效应跨导( g mb ),它描述了体效应如何影响漏极电流。我们可以这样计算:
$$g_{mb}~=~ \frac{\delta I_{D}}{\delta V_{BS}}~=~\frac{\delta I_{D}}{\delta {V_{TH}}} \frac{\delta V_{TH}}{ \delta V_{BS}}~=~g_{m} \eta$$
等式 6。
其中 η 是背栅跨导参数,通常具有 0 到 3 之间的值。
低频和高频型号
现在我们已经定义了参数,我们可以构建一个代
表晶体管小信号操作的电路模型。图 4 描述了 MOSFET 在低频下的小信号行为。
小信号 MOSFET 模型,适合低频运行。
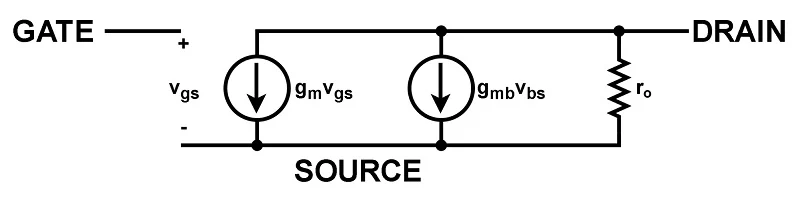
图 4. MOSFET 小信号模型。
在较高频率下,我们需要考虑 MOSFET 的寄生电容(图 5)。
带有寄生电容的MOSFET。
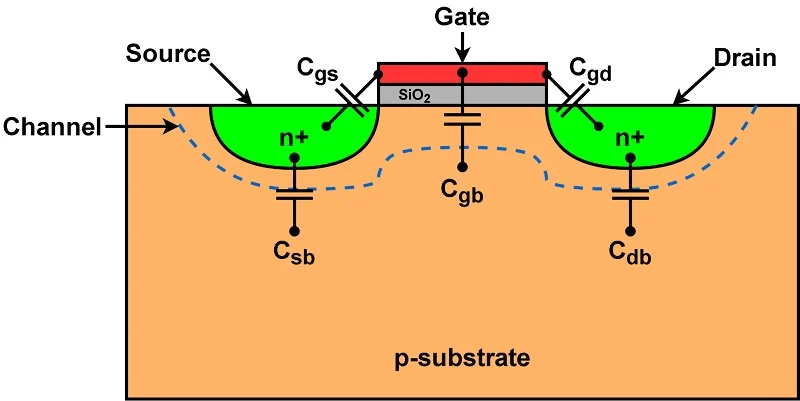
图 5.具有寄生电容的 MOSFET 结构。
上面代表的有:
C gs,栅源电容。
C gd,栅漏电容。
C gb,栅体电容。
C sb,源极至体电容。
C db,漏极至体电容。
图 6 中的小信号晶体管模型包括除体电容之外的所有这些非理想情况。
带电容的 MOSFET 小信号模型。

图 6.带有电容的 MOSFET 小信号模型。
从图6中我们可以看出,图3中MOSFET的固有增益具有单极点低通传递函数。现在我们可以计算晶体管的带宽,在本例中就是电压增益等于 1 (0 dB) 时的频率。这称为单位增益频率( f T )。
为了找到f T,我们将输出短路到地并计算图 6 的跨导。这样做可以得出以下等式:
$$f_{T}~=~\frac{g_{m}}{C_{gs}~+~C_{gd}}~ \propto ~ \frac{V_{D,sat}}{L}$$
等式 7。
从公式 4 和公式 7 中我们可以看出,要增加增益,我们需要增加晶体管的长度。然而,我们也看到这会导致带宽降低。反之亦然:减少晶体管的长度会导致更高的带宽。





