负载牵引测量是一种通用技术,其中呈现给被测设备 (DUT) 的负载阻抗会系统地变化。然后记录每个负载值的性能,并使用该数据来获取感兴趣的性能指标的恒定性能轮廓。
使用负载牵引技术,我们可以在阻抗平面上绘制恒定输出功率和效率的轮廓。使用史密斯圆图来完成此操作。图 1 显示了典型 PA 的输出功率 ( P out ) 和功率附加效率 ( PAE )的一些负载拉动轮廓。
功率放大器的功率附加效率(蓝色)和输出功率(红色)的负载牵引轮廓。
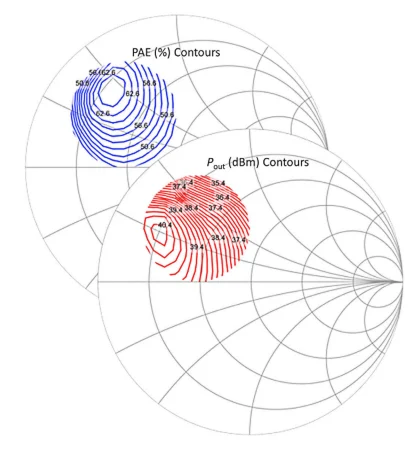
图 1. PA 的功率附加效率 ( PAE ) 和输出功率 ( P out ) 等值线。图片由罗德与施瓦茨提供
负载牵引等值线使我们能够考虑器件的非线性响应,并且可用于设计 PA,就像我们在设计小
信号放大器时使用恒定增益或噪声系数等值线一样。它们还可以解释
放大器的封装寄生效应,但这基本上超出了本文的范围。
RF 设计软件工具通常包括专门为执行负载牵引测量而设计的仿真工具。这些工具在史密斯圆图上应用许多不同的负载阻抗,并对结果进行插值以构建恒定输出功率的轮廓。
如果我们有器件输出和封装寄生效应的等效电路模型,我们还可以相对容易地估计恒定功率的轮廓。在本文的其余部分中,我们将了解如何实现(不过,我们暂时将寄生效应排除在分析之外)。
估计恒定输出功率轮廓
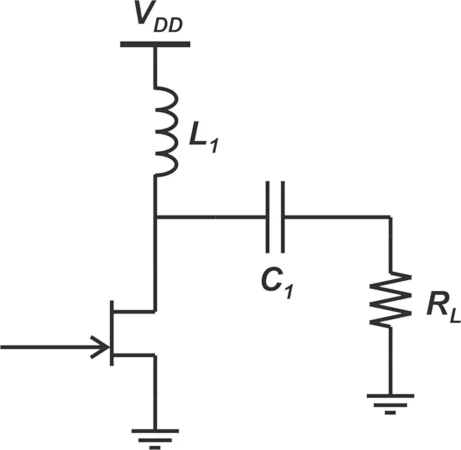
图 2 显示了围绕 FET 器件构建的A 类放大器。
A 类放大器的电路图。
图 2. A 类放大器示例。图片由 Steve Arar 提供
为了计算的目的,我们对此放大器做出以下假设:
它具有 3.5V
电源电压 ( V DD = 3.5V)。
其电流为 1 A(I max = 1 A)。
图 3 中的蓝色曲线显示了器件特性曲线的分段线性近似。
特性曲线的拐点电压( v k )远小于V DD。
一个假设对于分析来说并不是必要的,但它确实使解释一些相关概念变得更简单。
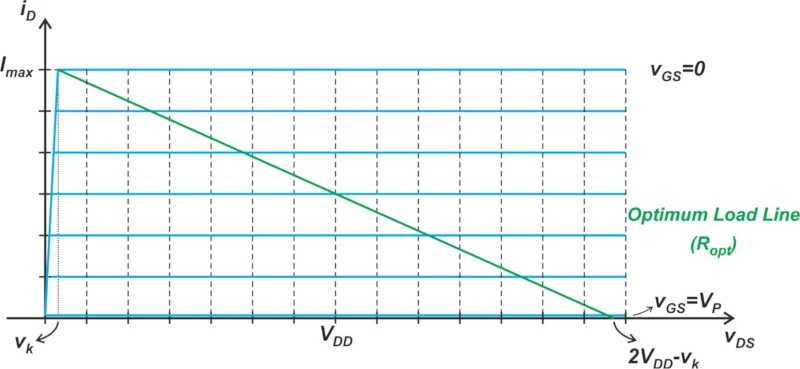
示例 PA 的特性曲线和负载线图。
图 3.示例 PA 的特性曲线(蓝色)和负载线(绿色)。图片由 Steve Arar 提供
首先,让我们找到示例放大器的负载和功率。为了获得输出功率,我们选择合适的负载电阻来偏置负载线中间的
晶体管。由于v k远小于VDD,偏置点为V DSQ = 3.5 V 和I DQ = 0.5 A。我们使用偏置点和图 3 中的信息来找到负载电阻:
Ropt = VDDImax2 = 2 × 3.51= 7 \欧米茄
等式 1。
和输出功率:
Popt = 12 × VDD × Imax2 = 12 × 3.5 × 12 = 0.875 W
等式2。
等式2。
该 PA 的输出功率为P opt = 0.875 W,实现的负载电阻为R opt = 7 Ω。
现在我们已经有了必要的信息,让我们找到该放大器产生 0.375 W 输出功率的负载终端。


