噪声是随机信号。这意味着无法根据其先前的值来预测其瞬时幅度。图 1 显示了一个示例。
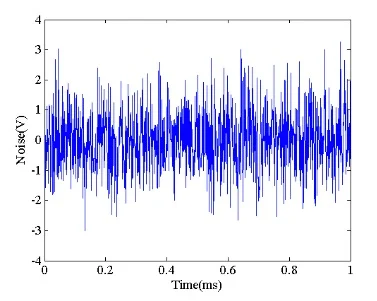
图1
如果噪声的瞬时幅度未知,我们如何确定其对系统输出的影响?尽管瞬时幅度不可预测,但噪声波形的其他属性是可以预测的。至少对于我们在电路设计和分析中通常必须处理的噪声源来说是这样。
让我们看看哪些属性是可预测的以及分析它们对我们有何帮助。
噪声幅度直方图
表征噪声源的步可以是估计给定值可能出现的频率。为此,我们从噪声波形中获取大量样本并创建幅度直方图。
例如,假设我们有 100,000 个噪声波形样本。根据这些样本的值,我们可以考虑噪声幅度的可能范围。然后,我们将可能值的整个范围划分为许多连续的非重叠幅度间隔(称为 bin)。直方图的箱(区间)通常大小相等。仓的高度由仓间隔内的噪声幅度值出现的次数确定。
图 2 显示了随机变量 100,000 个样本的直方图。在此示例中,直方图有 100 个 bin,和样本值分别为 4.34 和 -4.43。
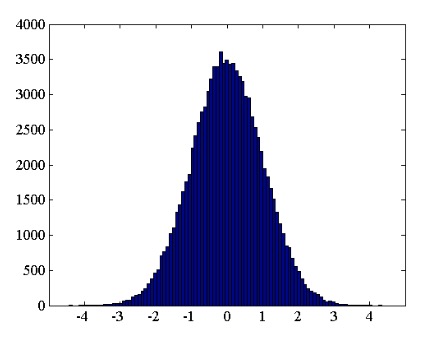
图2
上面的直方图显示了噪声幅度在给定间隔内出现某个值的频率。例如,直方图显示零附近的值更有可能出现。
估计幅度分布 上述直方图中的信息表示具有特定幅度值的可能性;然而,它是基于采集了 100,000 个样本的特定实验。我们通常需要一条与样本数量无关的似然曲线。因此,我们必须以某种方式对图 2 的信息进行标准化。
显然,所有的箱高都应该除以相同的值,这样得到的曲线仍然可以正确地显示不同幅度区间的相对可能性。但合适的标准化因子是多少呢?我们可以将 bin 高度除以样本总数 (100,000),以给出 bin 间隔出现的相对次数而不是其。然而,在曲线代表概率之前,仍然需要进行另修改。
如前所述,间隔的高度表示该间隔的连续范围内的噪声幅度值的总数。给定 bin 区间内的所有这些值均使用表示区间似然的单个数字来表示。虽然图 2 中直方图的值表示区间似然,但在概率论中,我们使用密度内涵来指定连续变量的似然。因此,为了获得正确显示概率密度的曲线,我们应该将箱高度除以箱宽度。该归一化曲线是可变概率密度函数 (PDF) 的粗略估计,这是基础随机过程的一个非常重要的特征。
我们可以通过稍微不同的方法得到相同的结果:根据我们的测量,噪声幅度在 -4.43 和 4.34 之间。实际上,噪声幅度可以取该范围之外的值;然而,我们正在使用测量数据来估计幅度分布。对于我们正在开发的粗略模型,值在-4.43和4.34之间的事件肯定会发生(其概率为1)。
该概率可以通过计算归一化曲线下的总面积(即估计的 PDF)来找到。为了使归一化曲线的总面积为 1,我们应该按等于总直方图面积的因子对箱高度进行归一化。直方图面积等于 bin 宽度乘以样本总数。因此,归一化因子等于箱宽度乘以样本总数。应用此归一化因子可以得到如图 3 所示的估计 PDF。
图3
平稳性假设
上述讨论是基于一个基本假设。它假设可以使用对随机过程的长期观察来估计其分布函数。换句话说,随机信号所源自的分布函数不会随时间变化。实际上,一般情况并非如此,但对于我们感兴趣的噪声源来说它是有效的。如果随机过程的统计属性不随时间变化,则称为平稳过程。
计算平均值
随机变量的 PDF 使我们能够估计其样本均值。让我们考虑一个简单的例子。假设假设的随机信号 X 具有三个可能值:1、-2 和 3,概率分别为 0.3、0.6 和 0.1。我们如何找到该信号的平均值?一种方法是通过从信号中获取大量样本来估计平均值。在这种情况下,我们可以通过计算数据观测值的算术平均值来计算样本均值: ˉx=1NN∑i=1xi
其中 N 表示样本总数,xi表示第 i 个样本。请注意,我们得到的仍然是随机变量平均值的估计,因为信号是随机的,我们无法预测未来值。估计平均值的更好方法是基于使用不同结果的概率。
根据此示例给出的概率值,我们可以得出结论,如果我们长时间观察此随机信号,则在观察持续时间的大约 30% 内,它的值为 1。在我们观察持续时间的大约 60% 和 10% 内,信号的值分别为 -2 和 3。因此,我们可以使用不同结果的概率作为该结果的权重。我们获得:
E(X)=1\乘以0.3+(?2)\乘以0.6+3\乘以0.1=?0.6
其中 E(X) 表示随机变量 X 的期望。随机变量的期望可以被认为是对随机变量样本平均值的估计。离散随机变量 X 的期望由下式给出:
E(X)=∑全部xxp(x)
其中 X 表示随机变量,x 表示 X 可以取的值。p(x)表示X取值x的概率。对于连续随机变量,我们有以下方程:
E(X)=∑全部xxp(x)
正如您所看到的,PDF 允许我们预测噪声波形的平均值。随机变量的期望有时用μ表示。我们可以代入图 3 中的值来找到此示例的期望值;然而,目视检查揭示了零附近的对称性,我们可以预测该随机变量的平均值为零。
随机变量的方差
类似地,我们可以使用随机变量的 PDF 来估计其方差。如果我们有来自随机变量的 N 个样本,我们可以使用以下等式来计算样本方差:
E(X)=∫+∞?∞xp(x)dx
请注意,分母选择为 N-1,而不是更明显的选择 N。请参阅Anthony Hayter 的《工程师和科学家的概率与统计》第 7.2.1 节 ,了解使用 N-1 而不是的解释N。
使用给定结果的概率作为该结果与平均值之间距离的权重,我们得到:
s2=1N?1N∑i=1(xi?ˉx)2
对于连续随机变量,我们有以下方程:
E((x?μ)2)=∑全部x(x?μ)2p(x)
因此,PDF 允许我们预测噪声波形的平均值和方差。
方差和平均功率
当 μ =0 时,连续随机变量的方差简化为:
E((x?μ)2)=∫+∞?∞(x?μ)2p(x)dx
这是噪声样本平方值的期望。该值在概念上类似于确定性电压信号 s(t) 的平均功率,定义为
Pavg=limT→∞1T∫+T2?T2s2(t)dt
其中平均功率用 V 2而不是 W 表示。这个想法是,如果我们知道 P avg ,我们可以通过将 P avg除以R L轻松计算出传递给给定负载 R L 的实际功率。对于随机变量,我们不知道瞬时样本值。但是,我们可以使用期望概念来预测 x 2的平均值。因此,当 μ = 0 时,噪声波形的方差是噪声平均功率的估计。
正如您所看到的,PDF 允许我们提取一些宝贵的信息,例如噪声分量的平均值和平均功率。
虽然我们现在能够估计噪声的平均功率,但仍然存在一个主要问题:噪声功率在频域中是如何分布的?本系列的下一篇文章将讨论这个问题。
结论
噪声是一种不必要的干扰,会降低我们所需信号的准确性。要分析噪声对系统的影响,我们需要对其行为有基本的了解。噪声的瞬时幅度无法预测;然而,我们仍然可以为我们感兴趣的噪声源开发一个统计模型。例如,我们可以估计噪声的平均值和平均功率。该信息以及噪声功率谱密度 (PSD) 通常足以分析噪声对电路性能的影响。

