量化小信号时的高频谐波
之前,我们讨论过即使是理想的模数
转换器 (
ADC)在数字化低幅度信号时也会产生谐波分量。例如,通过量化幅度为
0.75 LSB(有效位)的 1.11 kHz 正弦波,我们在图 1 的时域中得到以下波形。
显示输入和量化信号的图。
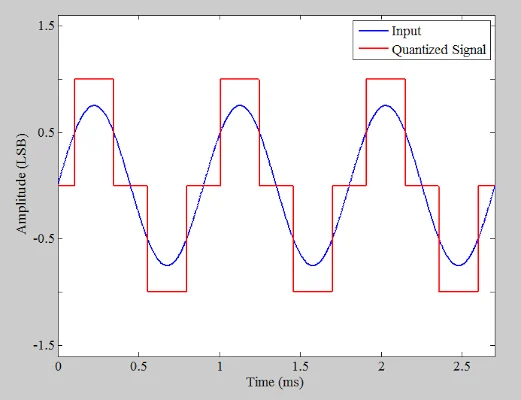
图 1. 显示输入信号和量化信号的图。
以 4 MHz 对量化信号(上面的红色曲线)进行采样并进行 FFT(快速傅立叶变换),我们获得下面的频谱(图 2 仅显示 DC 至 200 kHz 范围)。
fs = 4 MHz 的输出频谱。
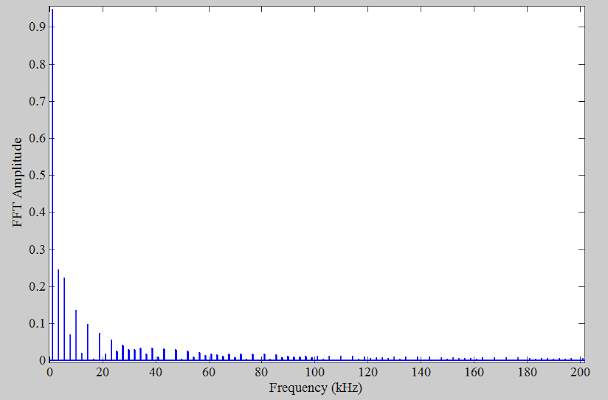
图 2. f s = 4 MHz时的输出频谱。
正如本文部分所讨论的,输出频谱中的谐波是量化操作的伪影。通过目视检查,我们发现这些谐波在高达 180 kHz 左右的频率下很容易辨别。为了产生上述曲线,我们故意使用远高于奈奎斯特采样定理所需的采样频率。这种高采样频率使我们能够获得信号的真实频谱,而不受有限采样频率的影响(就好像该信号是未采样的模拟信号一样)。
量化低幅度信号引起的混叠效应
如果我们使用较低的采样率(例如 40 kHz)来获取输出样本会怎么样?根据奈奎斯特采样标准,40 kHz 足以成功采样并重建 1.11 kHz 正弦波。然而,方波状信号具有高达 40 kHz 及以上的显着谐波分量。例如,第 33 次和第 35 次谐波(36.63 kHz 和 38.85 kHz)略低于我们的新采样频率 f s = 40 kHz(图 3)。
fs = 4 MHz 的放大频谱。
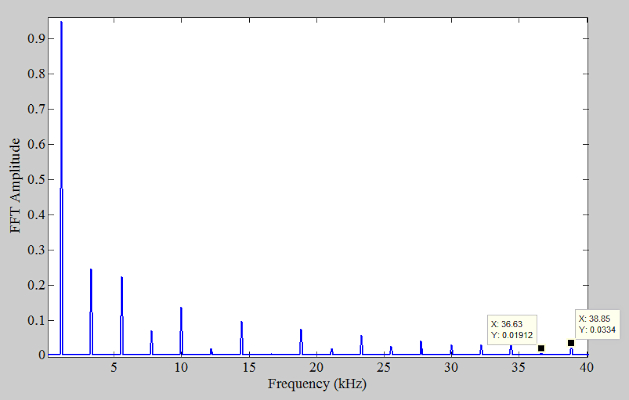
图 3. f s = 4 MHz时的放大频谱。
考虑到上述频谱,40 kHz 的采样频率实际上并不满足奈奎斯特采样条件。因此,通过以 40 kHz 采样,所有高于 20 kHz 的谐波都将被混叠回奈奎斯特间隔,频率可能是也可能不是输入的谐波。图 4 显示了采样频率为 40 kHz 时的输出频谱。
fs = 40 kHz 时的输出频谱。
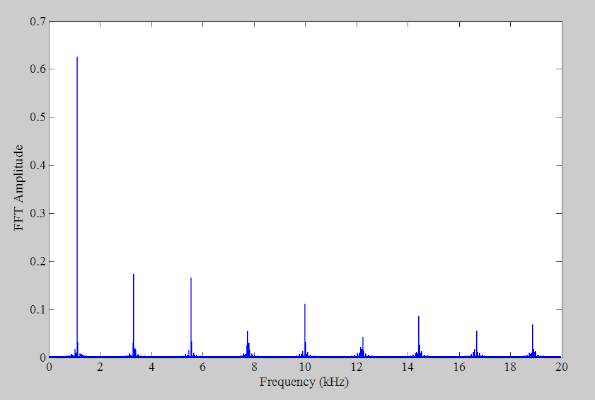
图 4. f s = 40 kHz时的输出频谱。
上述频谱中存在谐波和非谐波成分。从图 3 中,我们预计当使用 40 kHz 采样频率时,36.63 kHz 和 38.85 kHz 处的分量将分别混叠回 3.37 kHz 和 1.15 kHz。这些混叠分量如图 5 所示,它提供了感兴趣频率周围的输出频谱的放大版本。
感兴趣频率附近的输出频谱的放大版本。

图 5. 感兴趣频率附近的输出频谱的放大版本。
在信号中添加抖动噪声可以打破量化误差与输入之间的相关性,从而消除量化失真。因此,当 40 kHz 采样频率与抖动一起使用时,我们预计谐波和非谐波分量会消失。为了验证这一点,我们在量化之前向输入添加三角分布的噪声,然后以 40 kHz 进行采样。三角形抖动 PDF(概率密度函数)的宽度取为 2 LSB。在这种情况下,获得以下输出频谱(图 6)。
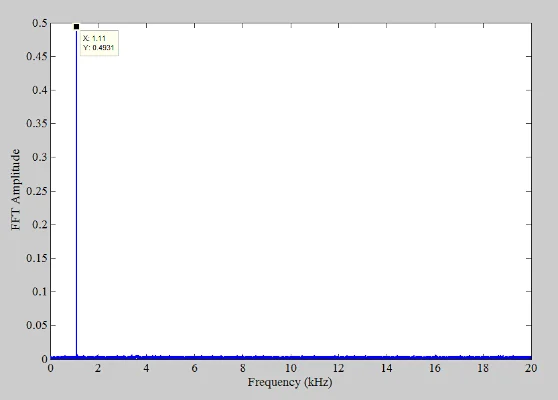
fs = 40 kHz 时抖动系统的频谱。
图 6. f s = 40 kHz 时抖动系统的频谱。
应用抖动后,输入频率处只有一个主要分量。现在我们已经熟悉了抖动的功能,让我们看一下应用该技术的不同方法。





