大多数
运算放大器的开环增益表现出恒定的增益带宽积(恒定英镑)。这种恒定性显着的结果是运算
放大器电路的噪声增益越高,闭环带宽就越低。例如,如果我们将运算放大器配置为同相放大器,在这种情况下,噪声增益与闭环增益A一致,则闭环带宽为
\[f_B = \frac {GBP}{A}\]
公式1
因此,如果我们使用 GBP = 1 MHz 的运算放大器并将其配置为A = 10 V/V 的同相增益,则我们得到f B = 10 6 /10 = 100 kHz。当A = 100 V/V 时,我们得到f B = 10 kHz,当 A = 1,000 V/V 时,我们得到f B = 1 kHz。
如果我们想使用这个运算放大器作为音频
前置放大器,增益为 1,000 V/V,带宽为f B = 20 kHz(代表音频范围的上限),该怎么办?
显然,单个 1 MHz 运算放大器无法做到这一点,因此让我们看看是否可以借助第二个类似的运算放大器将f B从 1 kHz 提高到 20 kHz。图 1 显示了这一概念的流行实现。
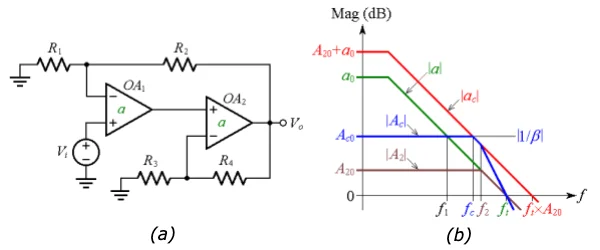
图 1. (a) 实现更宽带宽的复合放大器。(b) 直线波特图
在图中,您可以看到(a)一个复合放大器,以实现更宽的带宽。(b) 直线伯德图,其中:
| 一个| 是每个运算放大器的开环增益,ft是过渡频率(当前版本中ft = GBP)
| 一个c | 是复合放大器的开环增益
| 一个2 | 是OA 2的闭环增益,f 2是其 –3dB 频率
| 空调| _ 是复合放大器的闭环增益,f c是其 –3 dB 频率
|β| 是复合放大器周围的反馈系数
a 0、A c0和 A 20确定上述增益的 DC 值
这里,OA 1是主运算放大器,OA 2是辅助运算放大器,两者的开环增益均为a。OA 2配置为同相放大器,闭环增益为A 2,直流值为
\[A_{20} = 1 + \frac {R_4}{R_3}\]
公式2
由式1可知,将GBP替换为f t , OA 2的闭环带宽为
\[f_{2} = \frac {f_t}{A_{20}}\]
公式3
OA 1和OA 2共同构成一个复合放大器,其开环增益为
\[a_{c} = a\乘以A_2\]
公式4
OA 1反馈回路中OA 2的存在有两个影响:
它将开环增益从a扩展到c。由于分贝的对数性质(乘积的对数等于对数之和),DC 值a 0和A 20 按所示方式 相加。
它在f 2处建立了极点频率,这导致 | 的斜率 一个c | 曲线从 –20 dB/dec 更改为 –40 dB/dec,如图所示。该极点频率将侵蚀OA 1周围环路的相位裕度,因此我们必须警惕整个电路不会变得不稳定。
图 1(a) 的复合放大器又配置为同相放大器,反馈系数为β = R 1 /(R 1 + R 2 )。倒数 1/β 称为噪声增益,并且
\[\frac {1}{\beta} = 1 + \frac {R_2}{R_1}\]
公式5
(回想一下,对于同相运算放大器,噪声增益和闭环增益一致,因此 A c0 = 1/β)。如果OA 1单独运行,其闭环带宽将为f 1(见图 1(b))。
然而, OA 2的存在将闭环带宽从f 1扩展到f c,其中f c是| 的交叉频率。一个c | 和|1/β| 曲线。我们希望利用的正是这种带宽扩展。
为了获得更深入的了解,请考虑图 2 中的 PSpice 电路,该电路模拟闭环增益为 1,000 V/V 或 60 dB 的复合放大器。
使用拉普拉斯模块模拟 1 MHz 运算放大器的复合放大器的 PSpice 电路
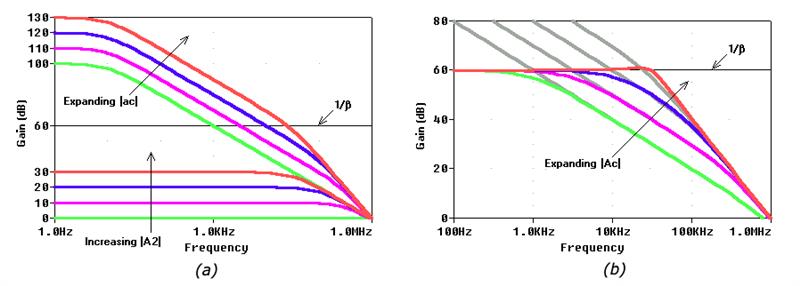
图2 . 用于使用拉普拉斯模块模拟 1 MHz 运算放大器的复合放大器的 PSpice 电路。
图 3(a) 显示了步进 EOA2 闭环增益 |A2| 的效果 通过 R4 以 10 dB 增量。对于|A2| = 0 dB 情况就好像 EOA1 单独运行一样,闭环直流增益为 1,000 V/V (= 60 dB),闭环带宽为 1 kHz。

对复合放大器开环和闭环增益的影响
图 3. 可视化EOA2闭环增益 |A2|中 10 dB 增量的效果 图 2 电路中的效果。对复合放大器 (a) 开环增益 |ac| 和 (b) 闭环增益 |Ac| 的影响。
增加|A2| 扩大复合放大器的开环增益|ac| 沿垂直轴和水平轴,同时减少EOA2 的闭环带宽f 2,如公式 3 所示。
图3(b)显示了对复合放大器闭环增益A c的影响:所有曲线都表现出相同的60 dB DC值;然而,带宽随着 |A2| 的增加而增加。
有趣的是,在图 4(a) 中观察OA1和OA2如何以互补的方式合作,以维持 60 dB 的恒定 DC 值。

EOA2 闭环增益 10 dB 增量效果的可视化
图 4.可视化EOA2闭环增益 |A2| 中 10 dB 增量的效果 基于EOA1的闭环增益|A1| 在图2(b)的电路中。复合放大器的闭环增益|Ac| 相位裕度为 45° 和 65°。
作为 |A2| 上升,|A1| 下降的方式使得它们的 DC 值不断加起来达到 60 dB,即 0 + 60、或 10 + 50、或 20 + 40、或 30 + 30。然而,OA2的极点频率f 2也会下降,因此这样做会逐渐侵蚀OA1的相位裕度。我们能筹集多远|A2| 在f 2使复合放大器不稳定之前?这取决于我们愿意接受的相位裕度。
在没有OA 2的情况下,电路将符合第 1 部分图 2(a) 的1/β 1曲线对应的情况,表明相位裕度为? m = 90°。存在OA 2时,m根据以下公式被侵蚀
\[\phi_m = 90^\circ - tan ^{-1}\frac {f_c}{f_2}\]
公式6
现在,利用英镑的稳定性| 一个| 图1(b)的曲线,我们写
\[A_{c0} \times f_c = f_t \times A_{20}\]
公式 7
结合等式 3 和 7 并求解f c /f 2比率,得出以直流增益 A 20和 A c0表示的? m
\[\phi_m = 90^\circ - tan ^{-1}\frac {{A_{20}^2}}{A_{c0}}\]
公式8
转过方程 8,我们可以发现对于给定的? m和 A c0 ,我们可以将A 20增加多远
\[A_{20} = \sqrt{A_{c0} \times tan(90^\circ-\phi_m})\]
公式 9
一种流行的策略是施加f 2 = f c,这种情况对应于第 1 部分图 2(a) 的1/β 2曲线,其中? m = 45°。这是通过使A 20 = (A c0 ) 1/2来实现的。因此,对于图 2 的 PSpice 电路,我们需要A 20 = (1,000) 1/2 = 31.6 V/V,我们用R 4 = 30.6 kΩ 来实现。如图 4(b) 所示,随后的闭环增益在 22 kHz 左右出现一些峰值,并且在 40 kHz 左右出现 –3 dB 频率。
如果应用要求不出现峰值,那么我们会设定? m = 65°,这标志着峰值的开始。使用公式 9,我们发现A 20 = 21.6 V/V,我们在图 2 的 PSpice 电路中使用R 4 = 20.6 kΩ 来实现该值。随后的响应具有约 30 kHz 的 –3 dB 频率。这比 OA1 单独作用时产生的 1 kHz 带宽高得多。
值得指出的是,除了扩大带宽之外,OA 2的存在还使DC环路增益提高了A 20。在图 2 的电路示例中,如果没有OA 2 ,则f B = 1 kHz,直流环路增益为T 0 = βa 0 = 10 –3 ×10 5 = 100。存在OA 2并配置为A 20 = 21.6 V/V 使得? m = 65°,f B从 1 kHz 提高到 30 kHz,并且T 0从200提高到200× A 20 = 200×21.6 > 4,000,从而大大提高了DC精度。



