我们讨论了质量-弹簧-阻尼器(或质量-阻尼器-弹簧)结构可用于测量加速度。为了使验证质量位移与所施加的加速度成正比,应适当选择质量-弹簧-阻尼器系统的不同参数。本文将使用经典力学的概念来推导质量-弹簧-阻尼器系统的传递函数。
传递函数使我们能够描述检验质量如何响应外部加速度而移动。导出的传递函数将在本系列的后续文章中解释
加速度计的不同参数(例如
传感器工作线性范围和带宽规格)时使用。
然而,在尝试导出传感器传递函数之前,我们先简要介绍一下微机电系统 (MEMS) 技术,该技术使当今的小型、低成本惯性传感器成为可能。
MEMS 加速度计:使用质量弹簧阻尼结构测量加速度
用于传感加速度的质量-弹簧-阻尼器结构如图1所示。
MEMS 技术使我们能够在同一硅芯片上实现该机械系统的非常小的版本以及所需的信号调节电子器件,以拥有完整的传感解决方案。

图 1. 质量-弹簧-阻尼器结构
图 1. 质量-弹簧-阻尼器结构。
MEMS 技术借鉴了微电子行业基于光刻的微加工技术,并将其与其他制造技术相结合,从而能够在硅芯片上创建可移动部件。
微制造技术的进步有助于实现当今小型、低成本的微机械加速度计,图 2 所示就是一个例子。

图 2. CMOS MEMS 加速度计的扫描电子显微照片 (SEM)。图片由K.Zhang提供
在上一篇文章中,我们简要提到阻尼器在加速度计操作中起着至关重要的作用。在尝试导出质量-弹簧-阻尼器系统的传递函数之前,现在是更熟悉系统的这一重要部分的好时机。
MEMS 加速度计中的阻尼机制
阻尼器对耗散力进行建模,该耗散力会减少质量-弹簧-阻尼器系统的机械能并减慢检验质量的运动。
MEMS 加速度计的主要阻尼机制之一是运动质量与周围空气分子之间发生的内摩擦。事实上,可以在极低的压力下封装基于 MEMS 的加速度计,以减少空气阻尼的影响。然而,一般来说,空气阻尼是 MEMS 加速度计能量损失的主要来源。
其他常见的阻尼来源是结构阻尼和热阻尼。
结构阻尼考虑了 MEMS 器件中使用的组件结构引起的能量损失。
热阻尼对应于MEMS结构的应力应变关系随温度变化的偏差。阻尼器施加在检验质量上的总减速力通常被建模为与检验质量的速度成比例的力。
该力作用于质量运动的相反方向,由下式给出:
\[F_{阻尼器} = bv \]
其中b表示阻尼系数,v表示检验质量的速度。
请注意,当物体非常小时(微加工结构就是这种情况),空气阻力与物体的速度成正比。
一般来说,空气阻力与 物体的速度有复杂的关系。例如,大型物体(例如在空中移动的跳伞运动员)可能会受到与物体速度的平方成正比的阻力。
阻尼效果:理想还是有害?
由于阻尼源自耗散力,因此它可能看起来是一个应该避免的麻烦。事实上,许多 MEMS 加速度计被设计为仅具有少量阻尼(以降低系统噪声)。
但需要注意的是,没有阻尼的理想质量弹簧系统实际上是一个
振荡器,不能用作加速度计。
如果我们将“理想”弹簧质量系统的质量从平衡状态移开,然后释放它,即使没有向系统施加外部加速度,质量也会永远来回移动。这就是为什么对于加速度计,我们需要向弹簧质量系统引入至少少量的阻尼。
使用牛顿运动定律证明质量位移
假设如图 3 所示,传感器框架受到外力。
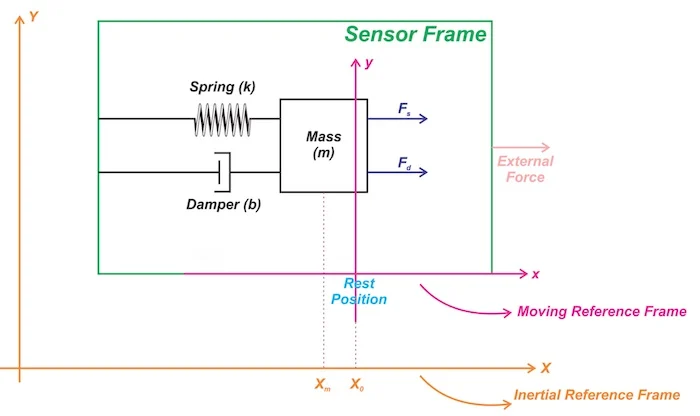
图 3. 质量-弹簧-阻尼结构传感器框架对外力的反应
图 3. 质量-弹簧-阻尼结构传感器框架对外力的反应。
为了根据所施加的加速度计算证明质量位移,我们使用牛顿第二运动定律。您可能知道,该定律指出,由净力产生的物体的加速度与净力的大小成正比,与物体的质量成反比。
这可以用下面熟悉的等式来表达:
\[F=马\]
公式1
其中 F 是施加到物体上的净力,m 是物体的质量,a 表示加速度。
为了正确地将这个方程应用到我们的系统中,这里应该注意一个微妙的点。牛顿第二运动定律仅适用于惯性坐标系,即不加速的坐标系。
图 3 描绘了我们的加速度计的两个不同的坐标系。橙色坐标系对应于解决物理问题时假定为惯性的地球参考系。
然而,洋红色坐标系表示固定到传感器框架的参考系。
该坐标系是非惯性的,因为当向传感器施加外力时它会加速。因此,要找到检验质量的运动方程,我们应该使用惯性参考系(橙色坐标系)。
什么力作用于证明质量?
假设如图3所示,X 0和X m分别表示检验质量块的静止位置和检验质量块在任意特定时间的位置。当正 X 方向的外力作用时,传感器框架向右加速。初,检验质量由于其惯性而倾向于“向后移动”。这会改变检测质量相对于传感器框架的相对位置,并将弹簧压缩 X 0 – X m。压缩弹簧对检验质量施加力并将其推向右侧。
弹簧施加的力由下式给出:
\[F_s = k (X_0 - X_m) \]
等式2
当检验质量偏离平衡时,阻尼器施加与检验质量相对于静止位置的相对速度成比例的力,我们得到:
\[F_d = b (\点 X_0 - \点 X_m) \]
公式3
在上面的方程中,点符号用于显示变量相对于时间的一阶导数。请注意,位置的导数是速度。
应用方程 1,我们得到:
\[F_s + F_d = ma_{证明质量} \]
代入方程 2 和方程 3,我们得到
\[ k (X_0 - X_m) + b (\dot X_0 - \dot X_m) = m \ddot X_m \]
公式4
在此等式中,双点符号表示 X m对时间的二阶导数。请注意, m是检验质量的加速度。
求非惯性参考系中的运动方程
需要根据检验质量相对于其平衡位置的位移来重写方程 4。这是因为我们的传感方法在实践中测量了验证质量相对于其平衡的位移。
例如,如图 4 所示,电容式传感方法测量检验质量相对静止位置的位移。
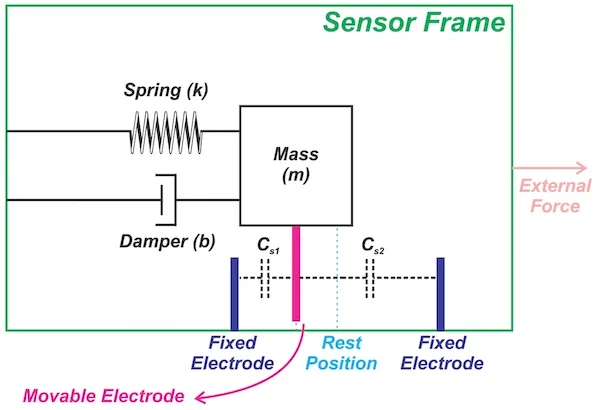
为了用证明质量位移来表达方程 4,我们需要使用图 3 中洋红色坐标系所示的移动参考系。我们使用小写字母 x 和 y 表示该坐标系。
如您所见,检验质量位移由 X m – X 0 = x给出。
在这种情况下,公式 4 简化为:
\[ -kx - b \dot x = m ( \ddot X_0 + \ddot x) \]
由于? 0 是传感器坐标系上的固定点,因此其二阶导数等于传感器坐标系a的加速度。这实际上就是我们要测量的参数。
因此,上式得出:
\[ m \ddot x + b \dot x + kx = -ma \]
寻找传递函数
应用拉普拉斯变换,我们可以找到加速度计的传递函数为:
\[ H(s) = \frac{x(s)}{a(s)} = \frac{-1}{s^2 + \frac{b}{m}s + \frac{k}{m }} \]
这是一个二阶系统。根据系统参数m、k和b的值,系统响应会有所不同。
例如,如果传感器帧加速度突然从零变化到有限值(阶跃输入),则系统的输出将接近其终值,其时间响应特性由系统参数确定。

图 5 显示了更改系统参数如何改变输出的振铃和稳定时间。在我们的讨论中,输出是证明质量位移。
图 5. 二阶系统的阶跃响应可能会根据系统参数的值而发生显着变化。
图 5.二阶系统的阶跃响应可能会根据系统参数的值而发生显着变化。图片由麻省理工学院的 David L. Trumper提供




