如果我们尝试将pn结焊接到np结,我们会得到如图 1 所示的器件,其中字母 E、B 和 C 分别表示发射极、基极和集电极。这些是分配给三个区域p、n、p的名称。
这样我们就创建了一个PNP 晶体管。
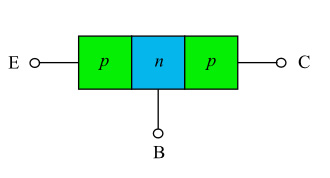
图 1:PNP 晶体管。 每个区域的大小是指示性的。
图 1:PNP晶体管。每个区域的大小仅供参考
相反,如果我们将np结焊接到pn结,我们就会得到如图 2 所示的器件,其中 E、B 和 C 在掺杂方面的作用颠倒了。结果是一个 NPN 晶体管。在两种配置中,器件均由连接点J E 和J C组成。
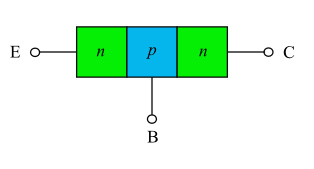
图 2:NPN 晶体管。
图 2:NPN晶体管
晶体管也被称为半导体
三极管,因为它标志着真空管的终结,就像结型
二极管取代了真空二极管一样。另一个常见名称是 BJT,是双极结型晶体管1的缩写。双极属性是指半导体中的导电性(由
电子和空穴给出)。
在图3中,我们可以看到PNP晶体管的电路符号,其呈现方式是为了突出与图1中的关系图。同样,图4显示了NPN晶体管符号。
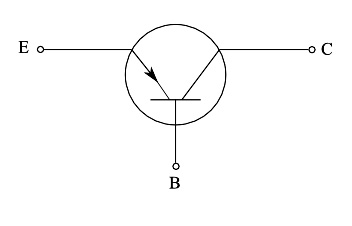
图 3:PNP 晶体管的电路符号。
图3: PNP晶体管的电路符号
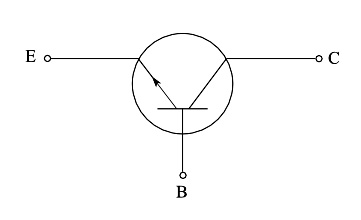
图 4:NPN 晶体管的电路符号。
图 4:NPN晶体管的电路符号
开路晶体管
让我们参考PNP晶体管(结果立即推广到NPN晶体管)。在开路条件下,我们期望与单结类似的行为,即存在接触电势(请参阅前面的教程),这实际上是势垒,其目的是防止空穴从发射极扩散到基地。如果没有这样的屏障,这些洞就会无限地向基地延伸;显然是非物理情况,因为我们处于开路条件下。如果 V 0是结点 J E处势垒的高度,类似的论证将导致我们说结点 J C上存在势垒 V'。假设各个区域 p,n,p 具有相同的杂质浓度,我们有 V 0 = V′。
热平衡的实现将通过单个区域的少数载流子浓度的恒定值来表征:

电力电子科学笔记:PNP 和 NPN 晶体管
使用以下约定:主字母表示载流子(电子、空穴),个下标表示其所属区域。例如,符号n p 告诉我们正在考虑p区域中的电子(因此少数电荷)。,第三个下标0表示系统在温度T 0(不一定是室温)下处于热力学平衡。
应该注意的是,我们忽略了耗尽层(在之前的教程中讨论过),因为与双结层相比,它的大小可以忽略不计。
在p型区域中,浓度n相同,因为我们假设这些区域相同。如果在笛卡尔轴系统中,我们在横坐标上构成PNP晶体管的双结的线性尺寸,在纵坐标上单个区域中少数载流子的浓度(方程(1)),在热力学和开路平衡我们将得到如图 5 所示的趋势,其中我们假设p n 0 > n p 0。
还应该指出的是,少数载流子浓度和开路条件下严格恒定的趋势是平均操作的结果,因为这些量围绕平均值(即测量值)波动。
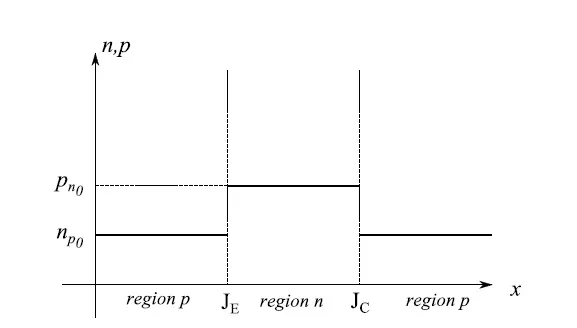
图 5:开路 NPN 晶体管中少数载流子浓度的趋势。
图5:开路NPN晶体管中少数载流子浓度的趋势
晶体管偏置
由于存在两个结和三个端子,因此极化组合比二极管更多。像往常一样,我们参考 PNP 晶体管,直接反向偏置J E 和J C。 在图 6 中,我们了这种极化配置,而图 7 是相应的电路图。准确地说,我们有一个电压发生器,其电压为V EB,而V CC 表示连接到J C 的电池产生的电压。我们用V CB 来表示集电极和基极之间的电位差。
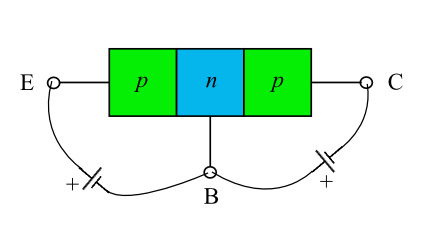
图 6:结点 JE 正向偏置,而 JC 反向偏置
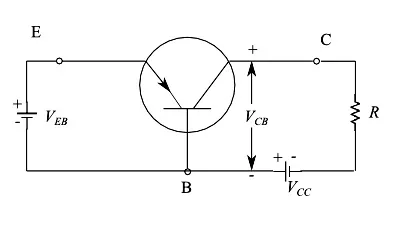
图 7:结点 JE 正向偏置,而 JC 反向偏置。
从发射极扩散到基极以及电子从基极扩散到发射极。因此,结果是J E的p和n两个区域中少数载流子浓度的宏观增加。
让我们把注意力集中在底座上广泛存在的洞上。在这里,我们在J C 附近具有以下电荷配置:如果我们测量 C 和 B 之间的电势差,我们会发现如图 7 所示的值,这意味着空穴被集电极 C“收集”。然而,J C 是反向偏置的,这决定了底部孔的指数阻尼,因此在J C 处,这些载流子的浓度在统计上为零。反过来,J C 的反向偏压会导致J C的p区电子浓度降低,这会以指数方式衰减J C 。C。如前所述, J E p区会增加,然后由于结中众所周知的少数载流子扩散机制而呈指数衰减。图 8 总结了这些结论。
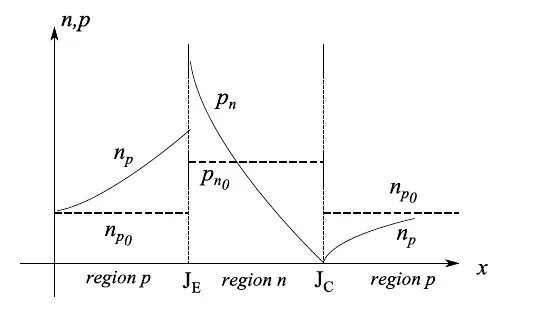
图8:闭路NPN晶体管中少数载流子浓度的趋势








