假设我们有一个大小为 512512 像素的 8 位灰度图像。我们需要应用以下传递函数来调整图像
亮度和
对比度:
Q [x, y] = a x I [x, y] + b
其中 a 和 b 被假定为常数已知值。假设我们希望有一个实现,当上述传递函数的输出超过 0 到 255 的范围时,使其输出饱和。
一种可能的实现如下所示。
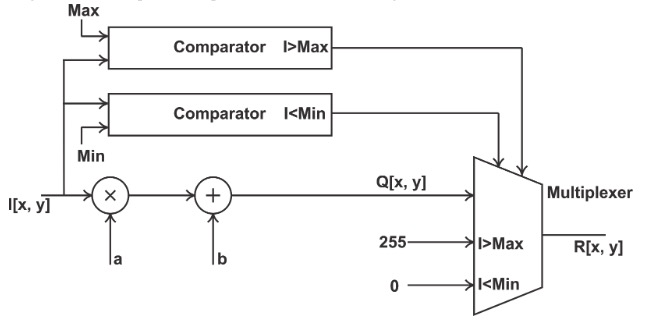
图2
由于我们假设 a 和 b 已知且恒定,因此我们可以确定将映射到 0 到 255 范围之外的值的阈值像素值。这些上限和下限在图中用“Max”和“Min”表示。上图。将输入像素值与这些阈值进行比较,并根据这些比较的结果,Q[x,y]、255 或 0 被传递到多路
复用器输出。处理整个图像需要多少次操作?有 512 x 512 = 2 18 个像素需要处理。
对于每个像素,我们应该进行乘法、加法和两次数字比较(我们忽略复用操作)。因此,总共需要4 x 2 18 = 2 20次操作!
是否有更有效的实现方式有望减少电路和/或功耗?
基于查找表的实现
除了使用逻辑门来实现给定点运算的传递函数外,我们还可以考虑基于查找表的实现。
当级联多个点操作时,基于查找表的实现变得特别高效。为了更好地理解为什么查找表可以成为实现逻辑本身的有效替代方案,我们应该注意,仅根据像素值处理图像的像素时可能会存在多次重复操作。
在上面的例子中,我们有 512 x 512 = 2 18 个像素需要处理。
在八位灰度图像中,一个像素只能取 2 8 个不同的值。考虑到像素总数 (2 18 ) 和一个像素可以具有的不同值 (2 8 ),我们可以得出结论,至少有一个像素值至少出现 \( \frac {2^{18}} {2^8}=2^{10} \) =1024 次在我们的灰度图像的矩阵中。
上图的逻辑实现以独立的方式处理所有像素,并且没有考虑其中许多计算是重复的。然而,注意到每个像素只能是具有 2 8 个不同级别的值,我们可以使用查找表来存储每个像素值的传递函数的输出。
因此,我们的 8 位像素值将连接到该查找表的 8 位地址。由于传递函数的输出是一个 8 位值,因此我们需要一个 256 x 8 位查找表来实现此示例。
使用查表法的好处
基于查找表的方法可以产生更有效的解决方案,特别是在级联多个不同点操作的情况下。这是因为,通过查找表,我们可以预先计算所有这些级联传递函数的终输出,并将这些终值存储在查找表中。
请注意,仅当设计未参数化并且我们能够预先计算给定输入像素值的输出时,才可以使用基于查找表的方法。然而,如果只有少量参数,我们仍然可以使用一些逻辑门和一些查找表的组合来实现更有效的实现。
