米勒频率补偿使得可以使用相当小的补偿电容C f值。这是非常理想的,不仅因为C f可以在片上制造,而且因为它比并联电容补偿更快的动态。之所以如此,是因为压摆率、开环带宽和全功率带宽大约 与C f成反比。
现在,就C的大小而言,对闭环增益一直补偿到单位增益是保守的。有许多应用涉及大于值的闭环增益,例如大于A min = 10 V/V,这将与更小的 C fo一起工作,从而享受更快的动态。
让我们使用正在运行的 PSpice 电路示例(在我关于
运算放大器频率补偿的文章中首次介绍)来比较失补偿与完全补偿:
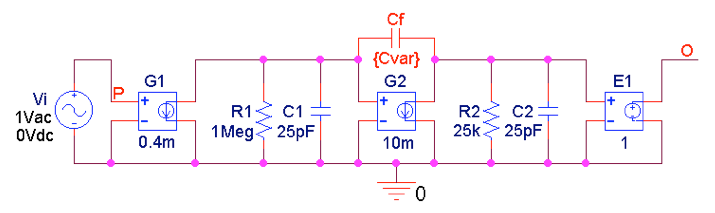
图 1. PSpice 电路绘制完全补偿和失补偿的开环增益。
PSpice的结果如下图所示:

图 2. 全补偿(闭环增益 ≥ 0 dB 时, C f = 9.90 pF)和失补偿(闭环增益 ≥ 20 dB 时, C f = 2.334 pF)的开环增益。两种补偿均享有? m ≥ 65.5°
结果得出以下观察结果:
在完全补偿( C f = 9.90 pF) 的情况下,0dB 增益的交叉频率f x ≈ 5.86 MHz,相位裕度? m = 65.5°。此外,如果我们将全补偿运算
放大器配置为 20 dB 闭环增益,则它的f x ≈ 633 kHz 和? m ≈ 87°,比 0 dB 增益有更大的余量。
失补偿( C f = 2.334 pF)时,20 dB 增益为f x ≈ 2.37 MHz(比完全补偿时的带宽更宽),并且? m = 65.5°。然而,如果我们将失补偿运算放大器配置为 0 dB 闭环增益,那么它的f x ≈ 11.1 MHz 和? m ≈ 24°,这是一个很差的余量,因为失
补偿器件的增益 ≥ 20 dB 。当? m ≈ 24° 时,20 dB 增益将表现出约 7% 的峰值和约 50% 过冲的瞬态响应,这两种情况通常都是不可接受的。
现在让我们继续考虑如何利用外部因素在电路中实现补偿;例如,
电阻器。
使用电阻器进行外部补偿
尽管失补偿运算放大器适用于高于A min 的闭环增益(在上述示例中, A min = 20 dB),但其卓越的动态特性使其对于增益低于A min的应用也具有吸引力。
但这会降低相位裕度? m,因此用户有责任对电路进行外部补偿,以将? m保持在所需水平。
为了说明这一点,我们将图 1 中的运算放大器设为失补偿形式,其中C f = 2.334 pF,并将其配置为电压跟随器操作,如图 3(a)所示。
(一) (二)
图 3. 电压跟随器:(a) 未补偿,(b) 外部补偿 ? m ≈ 65.5°。

如前所述,该电路的相位裕度仅为? m ≈ 24°。我们如何将其提高到? m = 65.5°?一个简单的解决方案是将其1/β曲线提高到 20 dB,同时仍然确保单位增益。我们通过以 1:9 的比例 连接电阻对R c -R f来实现这一点,如图3(b)所示。理想化极限a → ∞下的闭环增益仍然为
A_{理想}=1.0V/V
公式1
(这种情况是因为对于a → ∞,运算放大器输入
端子两端的电压趋于零。这意味着通过R c的电流为零,因此通过R f 的电流也为零。因此, R f两端的电压为零,所以我们有V o = Vi。)
然而,我们通过图4(a)的测试电路发现 反馈因子β 为
β=\frac{V_{n}}{V_{t}}=\frac{R_{c}}{R_{c}+R_{f}}=0.1
公式2
或1/β = 10 = 20 dB(请注意,在此示例中 1/β ≠理想值) 。

(一) (二)
图 4. (a) 用于查找图 3(b) 的电压跟随器的反馈系数 β 的电路,以及 (b) 波特图可视化。
响应如图 5 所示。

(一) (二)
图 5. (a) PSpice 电路,用于可视化 (b) 图 3 的电压跟随器的响应。拉普拉斯模块模拟图 2 的失补偿响应,通过 C f = 2.334 pF获得。
类似的推理过程也适用于图6(a)的单位增益反相放大器 。

(一) (二)
图 6. 单位增益反相放大器的外部补偿。
在这种情况下,在极限a → ∞下,我们有
A_{理想}=-\frac{R_{2}}{R_{1}}=-1.0V/V
公式3
经检查,现反馈因子为
β=\frac{R_{1}||R_{c}}{(R_{1}||R_{c})+R_{2}}=0.1
公式4
在这种情况下,选择R c以使( R 1 || R c )=R 2 /9。
电阻补偿的应用(和缺点)
上述专门针对单位增益同相和反相放大器的讨论可以很容易地推广到单位增益以外的闭环增益的情况,但仍然满足 1 < (1 + R 2 / R 1 ) < A min。
2999/R c = A值。
电阻补偿虽然简单,但有两个缺点:
任何可以用与同相输入串联的电压源建模的噪声(例如输入失调电压V OS)都会被放大1/β,因此也称为噪声增益。
环路增益T =(图 4(a)中的aβ = – V o / V t)减小(在本示例中减小了 10 倍),导致电路的闭环 DC 精度下降。
输入滞后补偿
我们可以通过将合适的电容C c与R c串联来减轻电阻补偿的限制,如图 7(a)所示的反相放大器。
(一) (二)

图 7. (a) 单位增益反相放大器的输入滞后补偿,(b) 波特图可视化。
请注意,为了确保所需的相位裕度,我们需要仅在交叉频率f x附近将放大器诱骗至所需的闭合率(ROC) ,而不必一直降至 DC。
物理上,1/β曲线在频率f c处断裂,此时电容阻抗的幅值等于R c或 |1/( j2πC c | = R c,给出
C_{c}=\frac{1}{2πR_{c}f_{c}}
公式5
为了防止相位裕度? m受到明显侵蚀,通常将f c放置在比f x低大约十倍的位置,或者
f_{c}≈\frac{f_{x}}{10}
公式6
对于图7(a)的电路 ,这意味着C c ≈ 54 pF。图 8 的仿真产生f x = 2.38 MHz 和? m = 61° 的测量值。

图 8 . (a) PSpice 电路,(b) 可视化单位增益反相放大器输入滞后补偿的稳定效果。
外部频率补偿的另一种方法
输入滞后补偿因在闭环响应中产生零极点双峰而臭名昭著,这会导致稳定时间特性过长等问题。Michael Steffes提出的替代补偿方法可以避免这些缺点, 如图 9 所示。

(一) (二)
图 9。 (a) Michael Steffes 针对失补偿运算放大器的补偿技术,(b) 波特图可视化。
我们在之前关于杂散输入电容补偿的文章中已经遇到过这种类型的电路,因此其中的许多考虑因素也适用于本电路,的区别是现在C 1是有意的。
我们有兴趣开发两个条件来指定C 1和C 2的值。在高频下, C 1和C 2的阻抗在幅度上比R 1和R 2小得多,我们可以忽略R 1和R 2并声明在高频下我们有1/β → 1 + C 1 /C 2。
施加 1 + C 1 /C 2 = 20 dB = 10 给出了我们电路示例的个条件
C_{1}=9C_{2}
公式 7
第二个条件源于以下事实:
C_{2}=\frac{1}{2πR_{2}f_{c}}
公式8
所以C 2的值取决于我们决定放置f c的位置。
在这里我们采用启发式方法,而不是应用Steffes的详细分析,这超出了本文的范围。
我们从方程 (6) 和 (8) 开始,并使用图 10 的 PSpice 电路来观察交流响应,同时保持方程 (7) 的条件,通过减小C 2逐渐增加f c 。

图 10. PSpice 电路绘制图 9a 的反相放大器的交流响应。要绘制瞬态响应,请将交流输入源更改为脉冲源。
当交流响应刚刚开始表现出峰值时,我们停止。这种方法给出C 2 = 12 pF 和C 1 = 9 C 2 = 108 pF,从而产生图 11 所示的良好响应。交流响应的 –3dB 频率为 2.36 MHz。
(一) (二)
图 11. 图 10 的反相放大器的 (a) 交流响应和 (b) 阶跃响应。

值得指出的是,通过改变C 1至9C 2 – C n的值,可以将反相输入端出现的任何杂散电容C n纳入该补偿方案中。因此,如果C n = 20 pF,那么我们使用C 1 = 88 pF。










