在本系列的上一篇文章中,我们看到压力
传感器是机械通气的关键要素。除了测量气道压力和大气压力外,
压力传感器还可以调节所输送呼吸的氧气浓度。
在本文中,我们将了解压力传感在机械通气中的另一个有趣的应用,即使用压差传感器测量气流。我们首先看一下流体力学的两个基本概念:伯努利方程和连续性方程。然后,结合这两个概念,我们将推导出一个将体积流量与压差值联系起来的方程。
假设流体流过具有不同横截面的管道,如图 1 所示。流体进入管道的左侧横截面并从管道的右端流出。
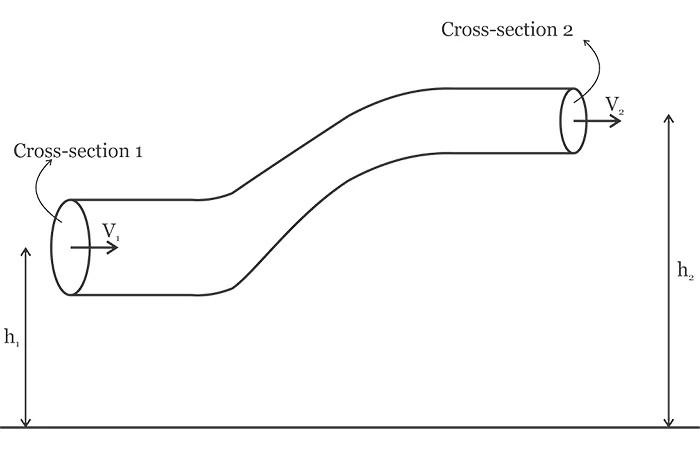
图 1.不同横截面的管道示意图。
上图中,h 1和h 2分别表示截面1和截面2处流体距地表的高度。当管道直径远小于管道高度时,我们可以假设给定横截面的所有流体颗粒几乎处于相同的高度。将能量守恒定律应用于截面 1 和截面 2 处的流体粒子,我们可以推导出以下方程:
\[P_1+\frac{1}{2}V_1^2+\rho gh_1=P_2+\frac{1}{2}V_2^2+\rho gh_2\]
其中 P 是流体压力,ρ 是流体密度,V 表示流体速度,g 是重力加速度。下标1和2的变量 分别对应于截面1和2处的流体参数。
上述方程通常被称为伯努利方程。这不是新的物理定律,而只是能量守恒定律的结果:管道输入处的能量应等于输出处的能量。伯努利方程的压力项与给定横截面后面的流体粒子对流体所做的功有关。
伯努利方程的第二项表示流体动能,第三项对应于其势能。关于伯努利方程的证明,可以参考这个伯努利方程推导视频。请注意,伯努利方程对于以非湍流、稳态方式流动的不可压缩、非粘性流体有效。
对于 \(h_1 \approx h_2 \) 的特殊情况,伯努利方程简化为:
\[P_1+\frac{1}{2}\rho V_1^2=P_2+\frac{1}{2}\rho V_2^2\]
公式1
连续性方程
根据质量守恒定律,质量既不能被创造,也不能被消灭。这一经典力学原理以及有关流体流动的一些假设可以帮助我们将流体流经的横截面积 (A) 与流体速度 (V) 联系起来。考虑流体 稳定流过具有变化横截面的管道,如图 2 所示。
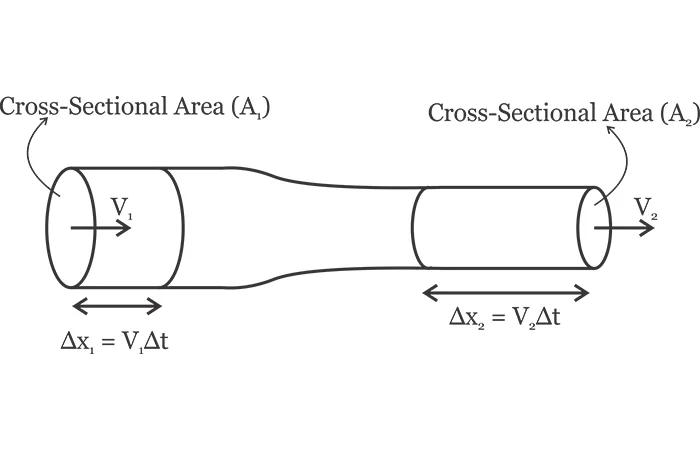
通过不同横截面的管道的稳定流动。
图 2.通过不同横截面的管道的稳定流量。
在稳定流动的情况下,给定点处流体的速度、密度和压力不随时间变化。
假设流体以\(V_1\)的速度进入管道左端。经过横截面积\(A_1\)的流体粒子将在\(\Delta t \)的小时间间隔后移动\(\Delta x_1 \)。
行进的距离可以用速度表示为 \(\Delta x_1 = V_1 \Delta t \)。也就是说,在 \(\Delta t \) 时间间隔内进入管道的流体体积为 \(A_1 V_1 \Delta t \)。将此值乘以流体密度即可得出进入管道的质量 \(\rho A_1 V_1 \Delta t\)。类似地,我们可以计算离开管道右端的质量为 \(\rho A_2 V_2 \Delta t\)。
根据质量守恒定律,进入管道的质量应等于离开管道的质量。因此,我们有
\[\rho A_1 V_1 \Delta t = \rho A_2 V_2 \Delta t\]
简化为:
\[A_1 V_1=A_2 V_2\]
公式2
该方程是一维流动的连续性方程。它指出横截面积和该横截面处的流体速度的乘积是恒定的。
上述推导基于关于流体流动的一些假设。例如,我们假设给定点的流体速度和密度不随时间变化(流动是稳定的)。此外,管道左端的流体密度等于管道右端的流体密度。换句话说,流体是不可压缩的。
根据压差计算流量
使用伯努利方程和连续性方程,我们可以找到每秒流动的流体体积。在流体动力学中,指定每秒流动的流体的立方米数(以 \(\frac {m^3}{s}\) 表示)的参数称为体积流量。根据这个定义,体积流量(用 Q 表示)由下式给出:
\[Q=\frac{体积}{时间}\]
在给定时间间隔 (\(\Delta t \)) 内流过管道横截面的流体体积可以表示为管道横截面积 (A) 乘以流体行进的距离的乘积(\(\Delta x \))。
\[Q=\frac{体积}{时间} =\frac{A\times \Delta x}{\Delta t} =AV\]
其中 \(\frac{\Delta x}{\Delta t}\) 被流体速度 V 代替。因此,我们可以通过简单地测量流体速度来计算流体的体积流量。可以通过将上述概念应用于具有不同横截面的管道来实现速度测量,如图 3 所示。
描述如何找到速度测量值。
图 3.描述如何找到具有不同横截面的管道的速度测量值。
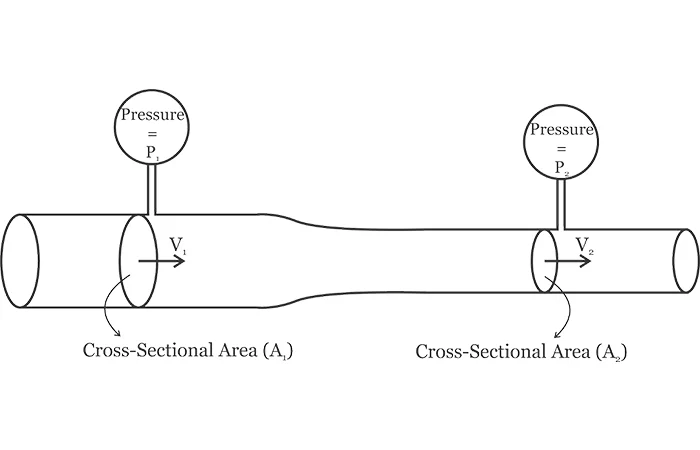
注意连接到压
力传感器的两个端口,用于测量管道上的压差。
根据方程 1,我们有
\[\Delta P=P_1-P_2=\frac{1}{2}\rho \left ( V_2^2-V_1^2 \right )\]
将方程 2 代入上面的方程得出:
\[\Delta P=\frac{1}{2}\rho V_2^2 \left (1-\left (\frac{A_2}{A_1} \right )^2 \right )\]
该方程将流体速度 (V2) 与压差和管道尺寸联系起来。现在,我们可以计算流体的体积流量 (Q):
\[Q=A_1V_1=A_2V_2=A_2\sqrt{\frac{\Delta P \times 2}{\rho \left (1-\left ( \frac{A_2}{A_1} \right )^2 \right )} }\]
公式3
测量气体的体积流量
伯努利方程和连续性方程都是基于流体不可压缩的假设推导的。一般来说,气体是可压缩的,我们不能用上述方法来测量气体的流量。
然而,当气体的速度充分低于声速时,气体密度的变化可以忽略不计,我们可以假设它是不可压缩的。此外,对于被视为不可压缩的气体,温度沿其流动路径不应发生显着变化。幸运的是,有一些应用可以满足这些条件,例如机械呼吸机中的气流。
测量机械呼吸机中的气流
一些呼吸机和肺活量计使用本文中描述的方法来测量进出患者肺部的空气。要试验此处讨论的概念,您可以 3D 打印一根类似于图 3 所示的管,但您可能需要进行多次实验才能找到合适的管尺寸。对于给定的管,方程 3 可以重写为
\[Q=A_2\sqrt{\frac{\Delta P \times 2}{\rho \left (1-\left ( \frac{A_2}{A_1} \right )^2 \right )}}=k_{系统}\sqrt{\Delta P}\]
其中 \(k_{system} \) 是一个将压差与气流相关的常数值。如果您可以使用一台在已知时间内吹出特定空气量的机器,您可以做一些实验来测量系统常数而不是计算它。
另一种解决方案是使用市售的气动装置。如图 4 所示,气动装置在气流中插入光幕,以产生与空气速度成正比的已知压降。
光幕插入气流中以产生与空气速度成比例的压降。
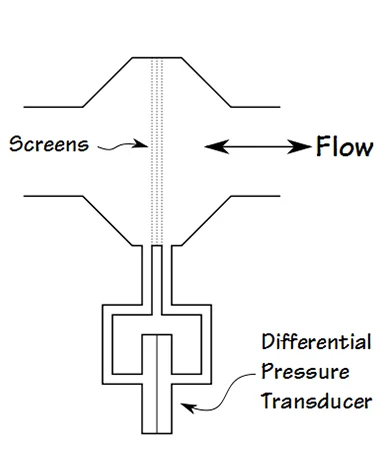
图 4. 插入气流中的光幕可产生与空气速度成比例的压降。图片由Richard Johnston提供 [ CC BY-NC 4.0 ]
您可以在 Richard Johnston 的有关气动流量测量基础知识的文章中找到有关此方法的更多信息。
结论
在本文中,我们介绍了一种测量机械通气中气流的方法。该方法基于流体力学的两个基本概念:伯努利方程和连续性方程。将这两个概念结合起来,我们得到了一个方程,将气流与管道上的压差联系起来。
除了此处讨论的技术之外,还有几种其他测量气体流量的方法。其中一些技术比其他技术更加线性,但没有一种技术是完全线性的。基于市售气动
流量计的
流量传感器是测量气体流量的线性方法之一。



