在本文中,我们将讨论在实践中,相位累加器的输出在传递到 LUT 之前应被截断。我们还将简要回顾一下相位截断对 DDS 输出光谱纯度的影响。
DDS的基本操作
假设我们想要生成一个数字化的正弦曲线。由于正弦波是一种周期性信号,因此我们可以将一个周期的样本存储在
存储器中,并使用这些样本生成我们想要的任意数量的周期。图 1 显示了一个示例,其中对模拟正弦曲线的一个周期采集了 16 个样本。使用这些样本,我们可以生成所需的周期信号。图 1 所示的时域采样实际上相当于量化正弦曲线的相位参数。
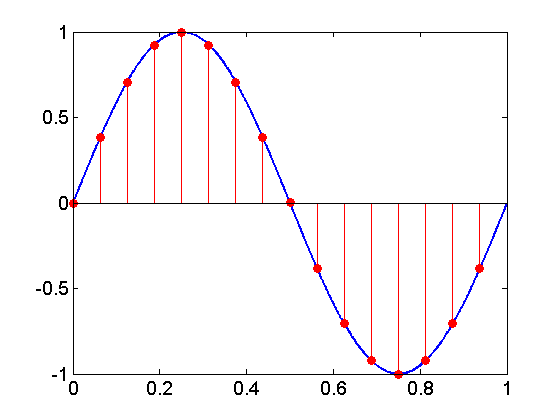
图1
在此示例中,使用 16 个不同级别来量化从 0 到 $$2 \pi$$ 的范围。
图 2 使用三角单位圆显示了该相位量化。

使用三角单位圆进行相位量化
图2
现在,假设我们将这 16 个样本存储在 ROM 中,并使用周期为 $$T_{clk} 的时钟信号顺序读取样本。每个样本将持续一个 T_{clk},因此需要 $$16 \times T_{clk}才能产生一个正弦曲线周期。如您所见,产生的正弦波频率将为 f_{out}=\
tfrac{1}{16 \times T_{clk}}。
请注意,对于给定的时钟频率,我们可以通过更改所使用的样本数量来更改输出频率。例如,如果我们顺序读取图 1 的 16 个可用样本(每隔一个样本)中的 8 个等距样本,则输出频率将增加到 $$f_{out}=\tfrac{1}{8 \times T_{clk}}$$。在本例中,我们正在读取图 1 的所有其他样本。换句话说,为了生成 $$f_{out}=\tfrac{1}{16 \times T_{clk}}$$,我们使用一个阶段表示 0 到 $$2 \pi$$ 范围的离散水平之间 $$\tfrac{2 \pi}{16}$$ 的增量;然而,对于 $$f_{out}=\tfrac{1}{8 \times T_{clk}}$$,离散级之间的相位增量增加到 $$\tfrac{2 \pi}{8}$ $。
这就是DDS的基本思想:我们在ROM中存储相对大量的样本,并以适当的相位增量顺序读取样本,以产生存储波形的不同频率。基于此讨论,我们获得了 DDS 的基本框图,如图 3 所示。
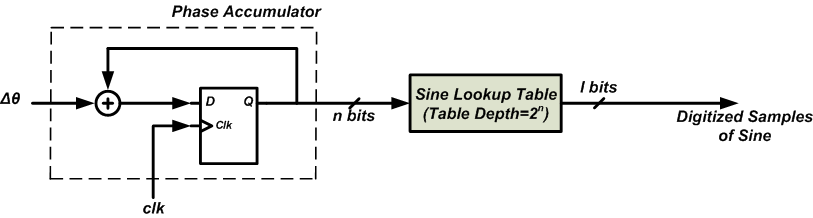
DDS 的框图
图3
如您所见,2^n正弦样本存储在查找表 (LUT) 中。LUT 的地址输入连接到称为“相位累加器”的块。“相位累加器”只是一个加法器,后面跟着一组 n 个
寄存器。如图所示,寄存的输出用作加法器的输入。因此,随着每个时钟沿,存储在寄存器组中的值将增加 $$\
Delta \theta$$ 的值。通过这种方式,我们可以控制从 LUT 读取的样本数量,并且我们将能够控制输出正弦波的频率。扩展上面讨论的简单示例,我们可以发现 DDS 的输出频率为
f_{out}=\frac{f_{clk}}{2^n}\times \Delta \theta
DDS 的频率分辨率
公式 1 显示 DDS 的输出频率是 $$\tfrac{f_{clk}}{2^n}$$ 的整数倍。将相位增量替换为其可能值,即 $$\Delta \theta =1$$,我们得到 DDS 的频率分辨率为
\Delta f=\frac{f_{clk}}{2^n}
公式2
公式 2 显示,对于给定的 $$f_{clk}$$,只能通过增加 n 来提高频率分辨率。这就是为什么需要具有大累加器的 DDS。例如,利用 n=48 的累加器,Analog Devices AD9912可以提供大约 3.6 Hz 的频率分辨率,同时以 $$f_{clk}=1GHz$$ 运行。
相位截断
大累加器可以产生任意小的频率调谐分辨率;然而,对于图 3 所示的结构,大型累加器要求使用不切实际的大 LUT。为了避免这个问题,我们通常截断累加器的输出。如图 4 所示。
具有截断累加器输出的框图
图4
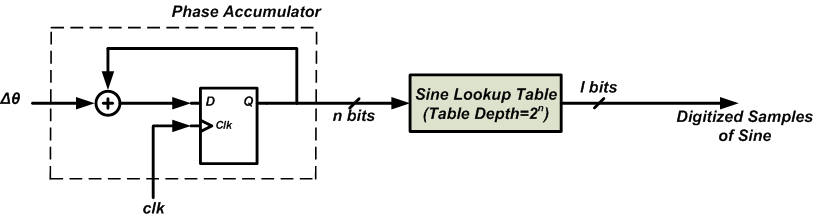
“量化器”接受累加器的 n 位输出,并仅将 p 个有效位 (MSB) 应用到 LUT。您可能想知道如果我们要丢弃一些 LSB 并仅将 p 个 MSB 应用于 LUT 的地址输入,为什么我们首先要使用大型累加器?
为了获得更好的理解,我们在图 2 的相位量化中再添加两位,但在访问 LUT 时丢弃这两位。我们的六位累加器的相位量化如图5所示。在该图中,红色圆圈代表累加器的四个MSB实现的相位量化级别,因此,两个相邻红色圆圈之间的相位差为$$\ tfrac{2 \pi}{16}$$。
正如您所看到的,黑点将两个连续的红色圆圈之间的每条弧线分为四个离散的级别。这些黑点对应于累加器的两个 LSB。两个相邻黑点之间的相位差为$$\tfrac{2 \pi }{64}$$。现在,假设累加器重置为零,并且图 4 中的 $$\Delta \theta =3_{10}$$。从累加器输出连续获得的离散级别将如图 5 的三角形所示。
从累加器输出获得的离散电平
图5
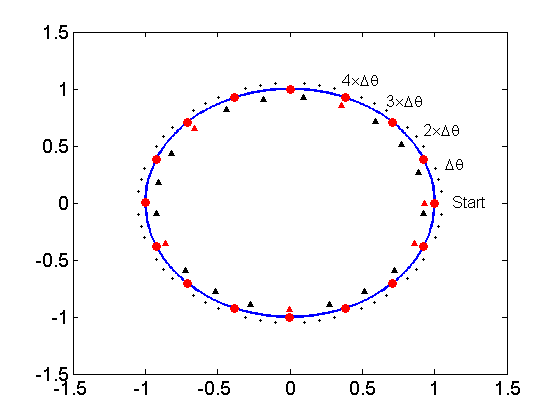
请注意,当三角形对应于黑点时,三角形为黑色;当三角形与红色圆圈重合时,三角形为红色。当累加器重置为零时,起始点将如图所示。
在下一个时钟沿,累加器输出将为三。正如您所看到的,这没有达到个红色圆圈的要求。因此,将传递到 LUT 的值将对应于 LUT 中存储的个样本(就像我们处于“起始”点时一样)。因此,截断过程此时会导致 $$3 \times \tfrac{2 \pi}{64}$$ 的相位误差。该相位误差将导致幅度误差,因为 LUT 将输出与“起始”点相对应的样本。
在下一个时钟沿,累加器将再增加 3,我们将达到 $$2 \times \Delta \theta$$ 指定的点。在这种情况下,截断的相位值将指向存储在存储器中的第二个样本。这次,相位误差将为$$2 \times \tfrac{2 \pi}{64}$$。
这个过程将继续下去,再添加两次之后,我们将达到 $$4 \times \Delta \theta$$ 点。该点的三角形显示为红色,因为它对应于从累加器的四个 MSB 获得的离散电平。此时,截断不会导致相位误差。
这个例子强调了三点:首先,无论我们是否进行相位截断,大累加器都会增加频率调谐分辨率。事实上,对于给定的 $$f_{clk}$$ 和 $$\Delta \theta$$,较大的累加器将需要更多时间溢出,并将产生更高分辨率的频率。
其次,由于我们截断了累加器输出,因此传递到 LUT 的相位信息可能会遇到一些错误。然而,该误差的值可能受到截断后保留的累加器位数的限制。这种有限的相位误差可以被设想为时基抖动。当我们增加图 4 中的 p 时,LUT 的深度将会增加,但由于相位截断而导致的误差将会减少。
总结这两点,我们以一些相位误差为代价来提高 DDS 的频率分辨率。这是一个有趣的想法,主要是因为我们可以通过将足够数量的累加器位传递给 LUT 来限制相位误差的值。
第三点,可以验证截断产生的相位误差是周期性的。在讨论的示例中,我们看到前四次相加的相位误差为 $$3 \times \tfrac{2 \pi}{64}$$、$$2 \times \tfrac{2 \pi}{64}$$ ,$$1 \times \tfrac{2 \pi}{64}$$ 和零。您可以验证该错误术语序列是否也会在下一个添加中重复出现。
相位截断杂散
相位截断产生的周期性误差会导致 DDS 输出信号幅度出现周期性误差。在输出频谱中,周期性幅度误差会产生不需要的频率分量,称为相位截断杂散。相位截断杂散的幅度和分布取决于三个参数:
累加器的大小 (n)
传递到 LUT 的累加器位数 (p)
相位增量的值 ($$\Delta \theta $$)
分析杂散的幅度,尤其是分布是相当复杂的。您可以在本书第 10.3.3 节中找到分析摘要。在此,我们仅回顾幅度分析的结果。根据此分析,相位截断杂散的幅度比所需输出的幅度低约 6.02p 分贝。例如,当 p=8 时,杂散将比 DDS 的所需输出低约 48 dB。如图 6 所示。
DDS输出频谱1
图 6. $$f_{out}=0.022$$Hz、n=p=8 和 l=12 时的 DDS 输出频谱。图片由
Xilinx提供。
值得注意的是,在基本的 DDS 结构中可以识别两种类型的量化: 1- 上面讨论的相位量化和 2- 幅度量化,对应于用于表示 LUT 中正弦曲线样本的位数。例如,通过增加图 4 中的 l,我们可以获得更好的正弦曲线样本近似值。
有趣的是,图 6 中所示的杂散电平取决于 LUT 的深度(即 p),而不是其宽度 (l)。例如,如果我们使用 l=16 位来表示正弦曲线的每个样本,并保持图 6 中所示的仿真的其他参数不变,则杂散电平将比 DDS 所需输出低约 48 dB。如图 7 所示。
DDS输出频谱2
图 7. $$f_{out}=0.022$$Hz、n=p=8 和 l=16 时的 DDS 输出频谱。图片由Xilinx提供。
概括
大累加器可以产生任意小的频率调谐分辨率;然而,这将要求使用不切实际的大 LUT。为了避免这个问题,我们通常截断累加器的输出。在这种情况下,我们以一些相位误差为代价来提高 DDS 的频率分辨率。这是一个有趣的想法,主要是因为我们可以通过将足够数量的累加器位传递给 LUT 来限制相位误差的值。
相位截断产生的误差是周期性的,会导致不需要的频率分量,称为相位截断杂散。相位截断杂散的幅度大约比所需输出的幅度低 6.02p 分贝。例如,当 p=8 时,杂散幅度将比 DDS 的所需输出低约 48 dB。




