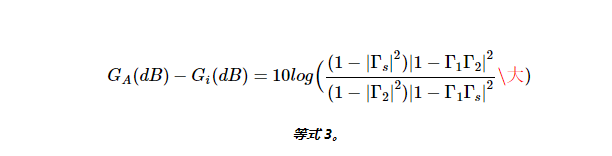可用功率增益 噪声系数定义中使用的功率增益是可用功率增益G A,其定义如下图 2 所示。可用功率增益是二端口网络 P AVN (图 2(a))可用功率与源 P AVS (图 2(b))可用功率之比。
可用功率增益定义 图 2. 可用功率增益定义 请注意,对于 P AVN 和 P AVS 测量,被测端口均连接至其共轭匹配负载。例如,为了找到P AVN ,模块输出连接到Zout =R out +jX out的复共轭,即Z L =R out -jX out。我们从公式 1 获得的功率并不是可用功率增益。为了区别于可用增益,它被赋予了一个特定的名称:插入增益,这将在下面讨论。 插入功率增益
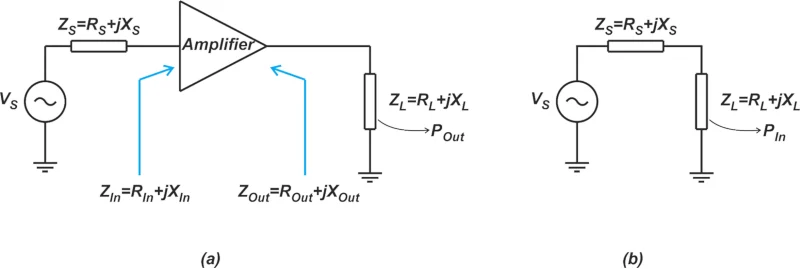
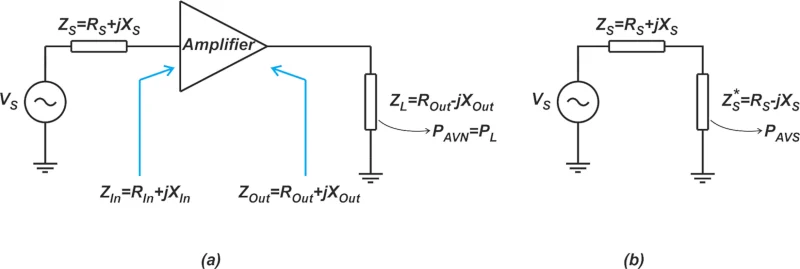
图 3 说明了插入功率增益的定义。 插入功率增益定义 图 3. 插入功率增益定义 插入功率增益取决于源阻抗和负载阻抗(Z S 和Z L)。如图 3(a) 所示,我们将 DUT 连接到 Z L ,同时其输入由 ZS 源阻抗驱动,并测量传递到负载的功率(在图 3 中用 P Out表示 )。我们还测量了源可以直接传送到 Z L的功率,在图 3(b) 中用 P In表示 。P Out 与 P In的比率 是 DUT 的插入增益。从这个解释中应该清楚,插入增益对应于当我们在给定 Z S之间插入 DUT 时获得的功率增益的变化 和Z L。 使用插入增益引入的误差 将 Y 因子方法的测量和校准步骤(图 1(a) 和 (b))与插入增益定义(图 3(a) 和 (b))进行比较,我们观察到从公式 2 获得的增益实际上是插入增益而不是可用增益。可以测量 DUT 的可用增益;然而,这需要两次额外的功率测量,其中必须将负载阻抗调整为与被测端口的共轭匹配。 然而,插入增益是从 Y 因子方法所需的四次功率测量中获得的。我们实际上假设插入增益等于可用增益。如果情况并非如此,我们的测量就会产生误差(公式 1)。可以看出,可用增益 G A 和插入增益 G i之间的差异 由下式给出: 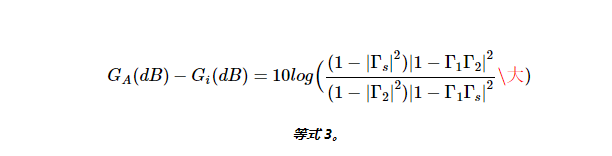
等式 3。 其中 Γ 1 是向噪声测量接收器观察的反射系数;Γ 2 是观察 DUT 输出时观察到的结果;Г s 是噪声源的反射系数(图4)。 噪声源、DUT 输出和噪声测量接收器的反射系数
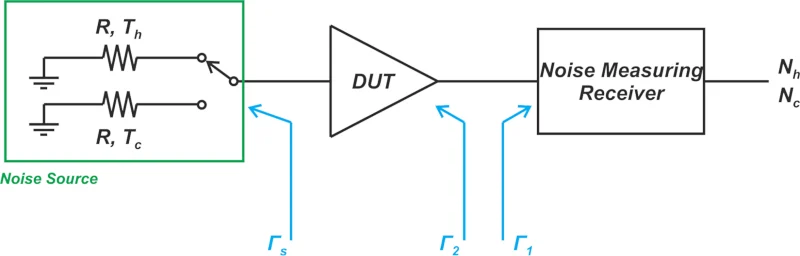
图 4. 噪声源、DUT 输出和噪声测量接收器的反射系数 请注意,在完美匹配的情况下(Г 1 =Г 2 =Г s =0),插入增益等于可用增益。在上面的等式中,需要了解反射系数的幅度和相位才能 从 G i找到 G A。通常情况下,相位信息是无法获得的,我们只能找到误差限。图 5 显示了插入增益和可用增益之间的差异,作为匹配级别的函数。
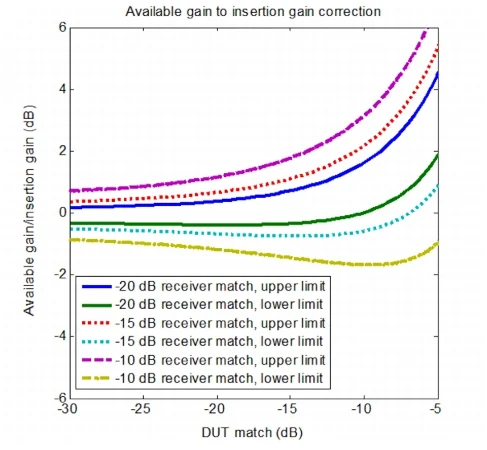
可用增益与插入增益之比作为接收器和 DUT 匹配的函数。 图 4. 可用增益与插入增益之比作为接收器和 DUT 匹配的函数。图片由Anritsu提供。 上图中,x轴是DUT输入和输出匹配(为简单起见,假设DUT的输入和输出匹配相同)。Y 轴是两个功率增益之间的差(以分贝为单位)。假设噪声源匹配为 -20 dB,并且假设 DUT 具有良好的隔离度 (|S21 × S12|= 0.1)。请注意,当 DUT 匹配度下降超过 -10 dB 时,两种增益之间的差异变得更加显着。在这种情况下,增益误差可能会在测量的 NF 值中引入显着的误差。 增益误差的 S 参数校正 此时,您可能想知道是否可以使用 DUT 的 S 参数以及公式 3 从插入增益中获取可用增益。通过将 G A (而不是 G i )代入 Friis 方程,我们可以校正增益误差。这看起来是有好处的,但有两点值得一提。 首先,请注意,我们通常没有反射系数(Γ 1、 Г 2和 Г s)的相位信息。对于标量测量,我们不知道矢量反射系数将如何组合以产生终误差。假设向量不匹配可用,我们可以 从 G i找到 G A。 然而,还有另一个问题可能会阻止我们进行更准确的测量:DUT 和测量设备的噪声系数是其驱动点阻抗的函数。图 5 通过假设 DUT 的噪声性能以图形方式说明了这一点。
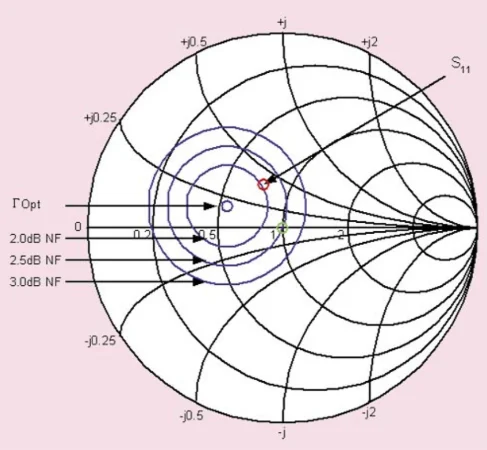
史密斯圆图展示了驱动点阻抗对噪声系数的影响。 图 5. 史密斯圆图展示了驱动点阻抗对噪声系数的影响。图片由D. Boyd提供。 当 DUT 由 50 Ω 源阻抗(对应史密斯圆图中心的绿色圆圈)驱动时,其噪声系数为 2.5 dB。然而,当源阻抗等于 DUT 的 S 11的复共轭 (图中红色圆圈标记)时,噪声系数为 2 dB。S 参数不向我们提供有关器件噪声性能的任何信息。因此,虽然 S 参数校正可用于 从 G i找到 G A,但它不允许我们考虑 DUT NF 的变化。如果不知道 NF 随源电阻的变化,S 参数校正甚至会增加 NF 测量误差。 确定噪声系数对源阻抗的依赖性需要专门的噪声系数测量设备,该设备使用短线调谐器将一系列复杂的阻抗应用于设备。然后分析这些测量结果,在史密斯圆图上生成 NF 的圆形轮廓,如图 5 所示。应该注意的是,常见的噪声系数分析仪和网络分析仪无法生成这些 NF 轮廓。 指定测量不确定度的必要性 如果没有噪声轮廓,则对噪声系数测量应用失配校正是无效的。在这些情况下,建议 尽可能减少不同端口的阻抗失配,然后将残余失配视为测量不确定度。除了失配效应之外,完整的不确定性分析还可以考虑其他非理想效应,例如测试设备的噪声系数的不确定性以及与噪声源本身相关的不确定性。不确定性分析是各种测量(包括 NF 测量)的关键。下表强调了通过比较两种不同的假设放大器来了解测量不确定度的重要性。 
在不考虑不确定性的情况下,人们会立即选择放大器 1 作为性能更高的设备。然而,考虑到测量不确定性,我们观察到放大器 1 的噪声系数高达 1.7 dB,而放大器 2 的 NF 为 1.5 dB。进行噪声系数测量时,需要注意的一个关键参数是测量不确定度。在以后的文章中,我们将讨论 Y 因子方法的测量不确定度。