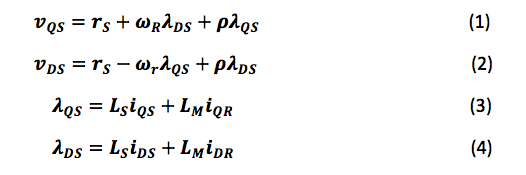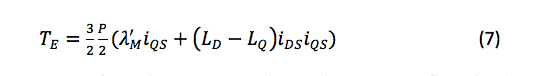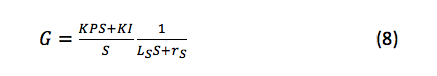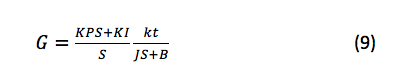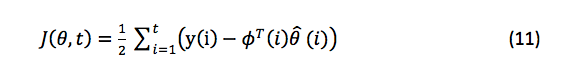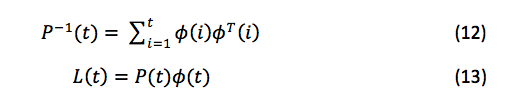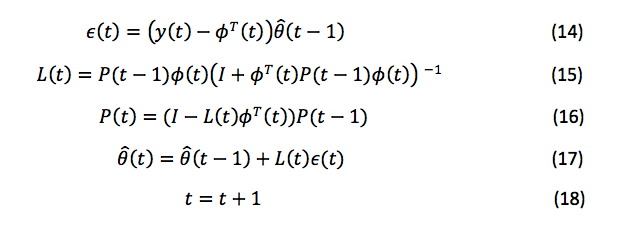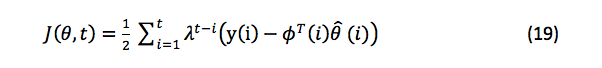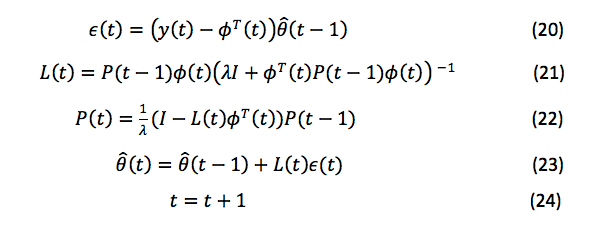永磁同步电机 (PMSM) 具有强大的机械动力学特性以及更高的效率和功率密度,因此在工业应用中非常普遍。在 PMSM 中,矢量控制包含电流环以及机械、电气、速度和位置环。然而,需要准确和的机器参数来为 PMSM
控制系统建立适当的数学模型。
数据表并不总是可用的,即使有,它们通常也不考虑每台机器遇到的操作条件。解决这一难题的一个简单方法是使用智能电机
控制模块。智能电机的算法应基于递归二乘 (RLS) 算法,并带有遗忘因子,使其能够实时修改和监控 PMSM 变化
本文介绍了使用智能电机控制模块为 PMSM 进行基于 RLS 的电机参数识别的解决方案。它还将演示对控制回路有影响的其他参数。
PMSM 中的磁场定向控制
通常,磁场定向控制 (FOC) 用于驱动 PMSM 以改善动态响应并充分发挥机器的潜力。基本目标是分别控制励磁磁通和转矩。在 Clarke 和 Park 变换之后,可以使用等式 1-4 在同步旋转 QD 框架下计算 PMSM 模型:
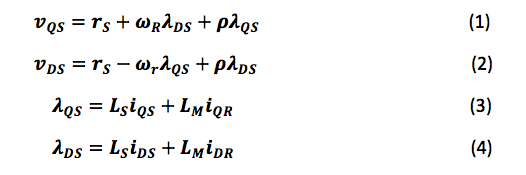
同步旋转QD框架下PMSM模型计算方程
其中下标Q和D分别指代Q轴和D轴变量。L S是电机的自感,L M是电机的互感。
为了进一步简化控制,转子磁通应在 D 轴上对齐,而 Q 轴上的转子磁通为零。Q 轴和 D 轴的通量可以分别用等式 5 和 6 估算:

用于估计 Q 轴和 D 轴通量的方程式
可以使用等式 7 计算电磁转矩:
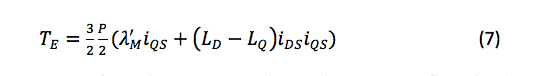
计算电磁转矩的方程式
按照上述方程式的变换步骤,磁通量可以直接由 D 轴电流控制。在 I DS恒定的情况下,可以通过操纵 Q 轴电流直接控制扭矩 (T E )。如果 I DS = 0,则电磁转矩与 I QS成正比。

PMSM 的磁场定向控制图图 1 PMSM 的 FOC 可以通过使用上述推导获得。资料
外环参考可以是所需的扭矩、机器速度或某个轴位置。它与测量变量进行比较,并将误差反馈给控制器(常见的是 PI 控制器)以生成命令转矩电流 (I Q-REF )。
D 轴电流参考 (I D-REF ) 根据磁通量要求设置。电流调节器和控制器的输出(V Q-REF和 V D-REF)是空间矢量脉宽调制 (SVPWM) 的输入。SVPWM 块为
逆变器生成栅极信号以驱动 PMSM。
为了实现 PMSM
伺服电机所需的动态性能,智能电机控制模块可以提供具有自动调整功能的受控参数。智能电机控制模块可以根据给定的带宽要求自动调整每个 PI 控制器。
对于电流环路,开环传递函数可以使用等式 8 估算:
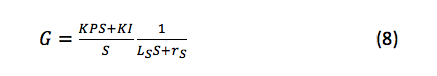
估计开环传递函数的方程
鉴于电流带宽等于 S = jω,可以根据定子电阻和
电感计算 PMSM 控制参数(KP 和 KI)。
与电流环类似,外环的开环函数可以用公式 9 计算:
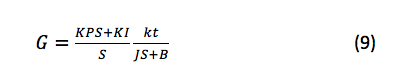
计算外环(机械环)开环功能的方程式
其中 kt 是机器扭矩常数,J 是惯性,B 是摩擦系数。
根据等式 9,可以使用机器转矩常数 (kt)、惯性 (J) 和摩擦系数 (B) 计算外环的控制参数。
递归二乘算法
RLS 是二乘 (LS) 回归算法的递归应用。每次迭代都会获取新数据以修改系统先前的估计。
系统输出 (y(t)) 可使用等式 10 计算:

计算系统输出的方程式
其中 是系统输入矩阵,θ 是 PMSM 系统参数。
使用 θ^ 表示估计的系统参数。目标函数,或要化或化的项,可以用等式 11 估算:
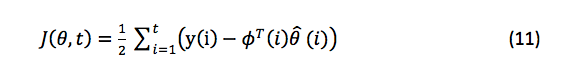
估计目标函数的方程
可以分别使用等式 12 和 13 计算 P 和 L 的新矩阵:
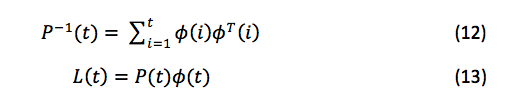
用于计算 P 和 L 的新矩阵的方程式
RLS 参数识别方案使用等式 14-18 估算:
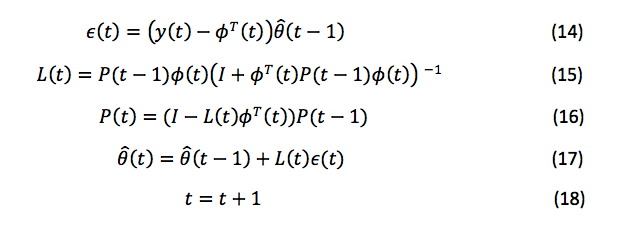
估计递归二乘参数识别方案的方程
向算法添加遗忘因子允许该方案处理时变系统。赋予遗忘因子数据的权重取决于数据的年龄,因为旧数据对当前迭代的影响较小。的数据被赋予算法的权重。遗忘因子 (λ) 的范围在 0 到 1 之间。可以使用等式 19 估算新的目标函数:
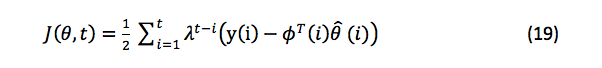
估计新目标函数的方程
使用等式 19 中的新目标函数,第 n 个旧的数据具有权重 λ n。可以使用等式 20-24 计算具有遗忘因子方案的递归二乘法:
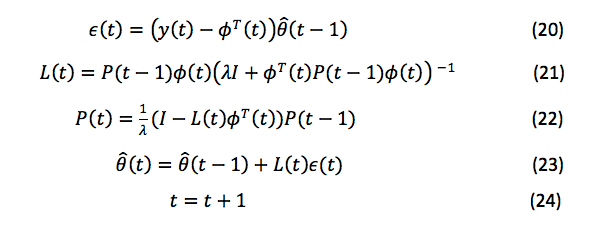
用遗忘因子方案计算递归二乘方程