对于信号失真，相位很重要

    讨论电子电路时，我经常锁定电路的幅值特性。例如，我们将滤波器称为高通、低通或带通，这是描述传递函数幅度形状的简写方式。很多时候，相位响应是事后才想到的，但这个被忽视的特性可能非常重要。 无失真传输在线性中并不意味着没有失真，我使用了无失真的定义：如果系统或网络的输出是其输入的副本，则系统或网络被称为无失真，除了幅度缩放和时间延迟 [参考资料 1]。从数学上讲，

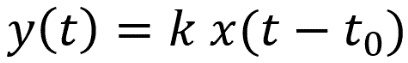
其中y ( t ) = 输出信号x ( t ) = 输入信号k = 幅度比例因子t 0 = 系统中的时间延迟如前一篇文章所述，k 表示所有感兴趣频率的恒定增益。现在让我们看一下x ( t – t 0 ) 项，它表示时间延迟t 0。将傅里叶变换应用到等式导致增益因子k 仍然存在并保持不变。t 0 延迟变为频域中的线性相位项（指数项）。以秒为单位的特定时间延迟映射到与频率成线性关系的不断增加的相移。与较低的频率相比，较高的频率必须具有较大的相移。对于符合无失真定义的电路，传递函数必须具有线性相位。五次谐波方波在根据谐波求信号带宽中，我们构建了一个方波，其频率分量高达五次谐波（图 1). 波形包括基波、三次谐波和五次谐波——不存在偶次谐波。当然，它不是一个完美的方波，但它在近似方波方面做得很合理。五次谐波方波 是演示相移效果的便捷工具。

    方波图 1. 此方波由基频加上三次和五次谐波组成。

    图 2 显示了五次谐波方波的各个频率分量：基波、三次谐波和五次谐波。查看每个正弦波的相位，您会发现它们排列得恰到好处，形成了图 1 中的波形。的正弦波是基波，其值与所需的方波形状对齐. 三次和五次谐波的振幅较小，使波形的顶部变平并填充角落。

    方波元件图 2. 方波的各个分量：基波、三次谐波和五次谐波。

    图 3 显示了当我们通过将基波偏移 30 度来扰乱这种对准时会发生什么。（三次和五次谐波没有改变。）请注意，生成的波形具有与图 1 相同的频率分量，但相位变化会扭曲波形形状。
    方波失真图 3. 通过将基波相位移动 30 度而引入方波的失真。

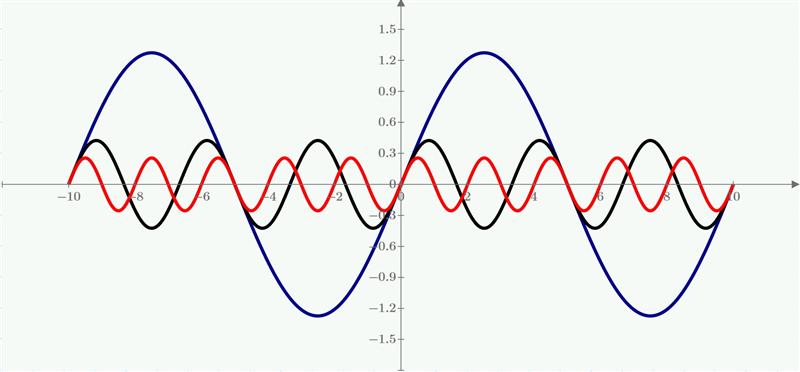
    如前所示，线性相移会延迟波形但不会引入失真。图 4 显示了应用了线性相移的相同五次谐波方波。基波再次偏移 30 度，而三次谐波具有三倍相移（90 度），五次谐波具有五倍相移（150 度）。我们看到了生成的波形，它与图 1 中的波形相同，但在时间上有所延迟。

    方波线性相移图 4. 对所有频率分量应用线性相移的方波。
    非线性相位导致失真我们已经表明，系统的相位特性会导致波形失真。由于方波含有谐波，因此方波是一种方便使用的波形，但其他波形也会以类似的方式受到影响。关键是线性相位响应（在感兴趣的频率范围内）将避免引入失真。