模拟 EE 世界失去了一颗明星。Jim 的数百篇文章、书籍和应用笔记是(并将继续是)信息、灵感和看到大师轻松解决棘手设计难题的喜悦的无底泉源,所有这些都包含在令人愉快的写作风格中。这里介绍的设计思想源自他发表在 AN45测量和控制电路集(夜班尿布和设计)第 7 页的电路之一。
用您独特的设计让工程界惊叹不已: 设计创意提交指南
在他的笔记中,Jim 讨论了使用
晶体管V BE tempco 作为廉价温度传感器的吸引力,但在实践中,它的实用性如何受到不可预测的晶体管到晶体管V BE可变性的限制。他解释了这个问题如何需要初始传感器晶体管校准(如果传感器需要更换则重新校准),这在很大程度上抵消了任何预期的便利和成本节约。
然后吉姆用一个巧妙的解决方案挽救了这一天。
Jim 说,事实证明,虽然随机晶体管的恒定电流 V BE不可预测,但 BJT V BE 随可变电流的变化是非常可预测的。具体来说,它可靠地服从这个简单的对数方程……
V BE = Tabs 198?V LOG 10 (I 1 /I 2 )
其中 Tabs = o开尔文的温度。因此,当用作温度计时……
Tabs = V BE 5050 / LOG 10 (I 1 /I 2 ) = 5050 ?V BE如果 I 1 /I 2 = 10
注意这个很酷(而且很容易记住)的“50-50”常量!
Jim 在图 1拓扑中应用了这种关系,据说将 10:1 偏置电流周期1置于 Q2 的二极管连接的 NPN 晶体管上,同步整流产生的 198?Vpp / o K AC 波形,然后放大和偏移产生的 DC 以产生0 到 10V = 0 到 100 o C,不需要传感器晶体管特定校准,输出。
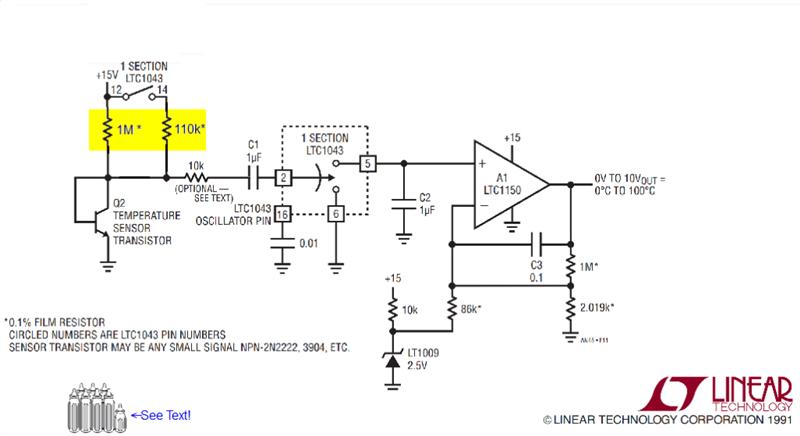
图 1 Jim Williams 的基于 V BE的温度计。
我在许多成功的测温应用中使用了“五十分”,并在图 2的O K 度到微秒振荡器中提供了这个想法的新变体。

图 2振荡器是温度计。
此处的?V BE 电流比由 R3/R4 电阻对(加上 R1+R2 积分器网络的一小部分贡献)设置为 16:1。这会在 A2 引脚 7 上产生一个与温度成比例的ΔV BE 周期性阶跃:每当 A1 比较器切换 Q2 FET 时,LOG 10 (16)/5050 = 238?V/ O K。我选择了较大的 16 与 10:1 电流比,以便为
运算放大器提供更容易处理的信号,并降低一些次要潜在误差源的重要性。C2 提供正反馈以确保比较器转换快速且干净。
然后,A2 积分器从?V BE 逐步回到 A1 的 500mV 设定点,如图 3所示,在 300 O K = 27 O C时生成持续时间T = 10?s/ O K = 3ms 的对称半周期超时。

图 3温度计振荡器波形。
尽管如 Willams 申请中所述,Q1 传感器晶体管本身不需要校准。微调器 R1 主要用作积分器
电容器 C1 和 Vdd 容差的单点补偿。一旦调整好R1,即使更换Q1也无需重新访问。
温度计振荡器的 0/5V 输出可通过标准微控制器定时器硬件方便地转换为数字温度读数。在1MHz的时钟速率下,一个振荡半周期T的转换分辨率为0.1 O。
一个拼写错误显然不知何故溜进了吉姆的原理图。据说设置 10:1 电流比并因此应为 9:1 电阻比的
电阻器对实际上是 549k/49.9k = 11:1,将设置 12:1 电流,因此比例因子为214uV/ oK;不是规定的 198uV。我不知道是否存在修正这个 8% 小问题的修订版,但这是一个简单的修正,我冒昧地做了。此外,Q1 是不必要的。


