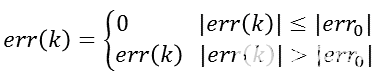PID控制器开发笔记之八：带死区的PID控制器的实现

    在计算机控制系统中，由于系统特性和计算精度等问题，致使系统偏差总是存在，系统总是频繁动作不能稳定。为了解决这种情况，我们可以引入带死区的PID算法。
    1、带死区PID的基本思想
    带死区的PID控制算法就是检测偏差值，若是偏差值达到一定程度，就进行调节。若是偏差值较小，就认为没有偏差。用公式表示如下：

 

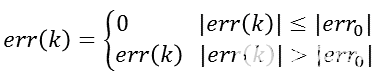
    其中的死区值得选择需要根据具体对象认真考虑，因为该值太小就起不到作用，该值选取过大则可能造成大滞后。
    带死区的PID算法，对无论位置型还是增量型的表达式没有影响，不过它是一个非线性系统。
    除以上描述之外还有一个问题，在零点附近时，若偏差很小，进入死去后，偏差置0会造成积分消失，如是系统存在静差将不能消除，所以需要人为处理这一点。
    2、算法实现
    前面我们描述了带死区的PID控制的基本思想。在接下来我们来实现这一思想，同样是按位置型和增量型来分别实现。
    （1）位置型PID算法实现
    前面我们对微分项、积分项采用的不同的优化算法，他们都可以与死区一起作用于PID控制。这一节我们就来实现一个采用抗积分饱和、梯形积分、变积分算法以及不完全微分算法和死区控制的PID算法。首先依然是定义一个PID结构体
    接下来我们实现带死区、抗积分饱和、梯形积分、变积分算法以及不完全微分算法的增量型PID控制器。/*定义结构体和公用体*/
    typedef struct
    {
    float setpoint;               /*设定值*/
    float kp;                     /*比例系数*/
    float ki;                     /*积分系数*/
    float kd;                     /*微分系数*/
    float lasterror;              /*前一拍偏差*/
    float preerror;               /*前两拍偏差*/
    float deadband;               /*死区*/
    float result;                 /*PID控制器计算结果*/
    float output;                 /*输出值0-100%*/
    float maximum;                /*输出值上限*/
    float minimum;                /*输出值下限*/
    float errorabsmax;            /*偏差值*/
    float errorabsmin;            /*偏差值*/
    float alpha;                  /*不完全微分系数*/
    float derivative;              /*微分项*/
    float integralValue;          /*积分累计量*/
    }CLASSICPID;
    接下来我们实现带死区、抗积分饱和、梯形积分、变积分算法以及不完全微分算法的增量型PID控制器。
    void PIDRegulator(CLASSICPID vPID,float pv)
    {
    float thisError;
    float result;
    float factor;
    thisError=vPID->setpoint-pv; //得到偏差值
    result=vPID->result;
    if (fabs(thisError)>vPID->deadband)
    {
    vPID-> integralValue= vPID-> integralValue+ thisError;
    //变积分系数获取
    factor=VariableIntegralCoefficient(thisError,vPID->errorabsmax,vPID->errorabsmin);
    //计算微分项增量带不完全微分
    vPID-> derivative =kd*(1-vPID->alpha)* (thisError-vPID->lasterror +vPID->alpha*vPID-> derivative;
    result=vPID->kp*thisError+vPID->ki*vPID-> integralValue +vPID-> derivative;
    }
    else
    {
    if((abs(vPID->setpoint-vPID->minimum)deadband)&&(abs(pv-vPID->minimum)deadband))
    {
    result=vPID->minimum;
    }
    }
    /*对输出限值，避免超调和积分饱和问题*/
    if(result>=vPID->maximum)
    {
    result=vPID->maximum;
    }
    if(result<=vPID->minimum)
    {
    result=vPID->minimum;
    }
    vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算
    vPID->lasterror=thisError;
    vPID->result=result;
    vPID->output=((result-vPID->minimum)/(vPID->maximum-vPID->minimum))*100.0;
    }
    3、总结
    引入死区的主要目的是消除稳定点附近的波动，由于测量值的测量精度和干扰的影响，实际系统中测量值不会真正稳定在某一个具体的值，而与设定值之间总会存在偏差，而这一偏差并不是系统真实控制过程的反应，所以引入死区就能较好的消除这一点。
    当然，死区的大小对系统的影响是不同的。太小可能达不到预期的效果，而太大则可能对系统的正常变化造成严重滞后，需要根据具体的系统对象来设定。