如何使用LTspice仿真来解释电压依赖性影响

    问题：

    如何在电路仿真中考虑多层陶瓷电容器(MLCC)的直流偏置影响？

    答案：

    使用LTspice的非线性电容功能和合理的模型。

    本文说明如何使用LTspice仿真来解释由于使用外壳尺寸越来越小的陶瓷电容器而引起的电压依赖性（或直流偏置）影响。尺寸越来越小、功能越来越多、电流消耗越来越低，为满足这些需求，必须对元件（包括MLCC）的尺寸加以限制。因此，电压依赖性或直流偏置的影响也受到关注。

    要实现陶瓷电容器的微型化，就必须在越来越小的空间内实现更高的电容值。为此，具有高介电常数(ε)和越来越薄的介电绝缘层的材料正在被实现，这使得现在有可能在工业级规模上生产高质量的陶瓷层。

    遗憾的是，介电常数εr = 是电场强度的函数，因此电容表现出电压依赖性。根据陶瓷类型和层厚度，这种影响可以非常显著。在很大允许电压下，电容下降到标称值的10％以下并不罕见。

    在将恒定电压作用于MLCC的应用中（例如去耦电容），很容易考虑此影响。只要电压保持恒定，就可以从制造商提供的数据手册或在线工具中获取剩余电容值。

    但是，对于电压可变的情况该怎么办？例如在图4中，开关稳压器上的输入滤波器采用5 V USB电源至24 V工业电源供电。另一个例子是，2线以太网PHY与相同线路上不同电压值的电源交流耦合。

    在此类情况下，使用LTspice进行电路仿真可提供有用的洞察。有些MLCC制造商已经提供了相应的直流偏置模型供加载。此外，LTspice提供了模仿电压依赖行为的方法及实施工具。对此，电容与电压关系的曲线及图3中描述的方法之一很有用。

    LTspice提供了一个众所周知的具有恒定电容的电容模型以及一个非线性模型。该非线性模型用于求解电荷方程。由于需要保留电荷，直接求解非线性电容模型是不合适的。但在这里，这不应该是问题，因为电容是通过电荷对电压微分来获得的。反过来，必须对电压相关电容进行积分。这已经针对如下方法完成，因此无需任何数学知识便可使用这些模型。

    一阶方法使用线性电压依赖性：

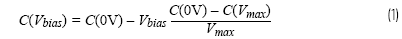
    从中通过积分可得出：

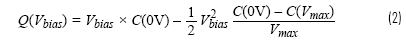
    Q=x*{c0V}-0.5*x**2*({c0V}-{cVmax})/{Vmax}.

    以上便是电荷方程。现在可以将其直接插入LTspice术语中，以代替电容器的电容值：

    Q=x*{c0V}-0.5*x**2*({c0V}-{cVmax})/{Vmax}

    然而，许多MLCC的近乎恒定的初始电容即使在中等电压下也会迅速降低，之后几乎保持恒定。在此类情况下，如果仅使用线性模型，则对于较大范围的电容，有效电容会被高估。对于这种分布广泛的情况，可以使用基于双曲正切(Tanh)的模型：

    无需进一步的辅助工具便可轻松估算参数。

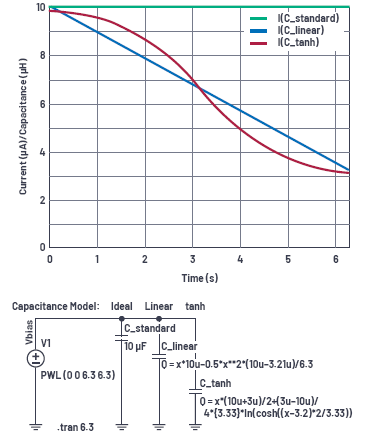
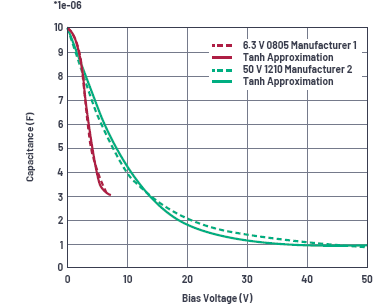
    图1.Tanh近似函数和相关参数

    电容值也可直接由电荷等效值取代

    Q=x*({C0 Csat})/2 ({Csat-C0})/4*{Vtra}*ln(cosh((x-{Vth})*2/{Vtra}))

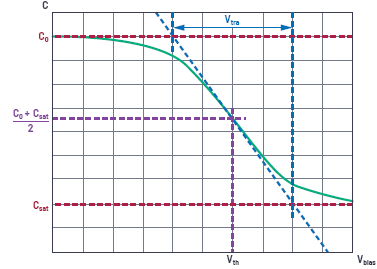
    图2.10 μF MLCC

    为了检查LTspice中的电容模型，应用了恒定电压斜坡。

    这样，通过电容的电流量便完全对应于电容值，因为：

    图3清楚地显示了所提出的非线性模型相对于标准恒电容模型的优越性。利用这种电容曲线，线性模型足以适用于大多数应用。

    图3.在LTspice中以不同电容模型仿真10μF 6.3V 0805 MLCC的示例

    很后应注意的是，这里仅仿真了单个非理想效应。MLCC仍然存在许多其他效应，包括老化、温度依赖性、频率依赖性、AC幅度依赖性、电介质吸收等。对于许多应用，将直流偏置依赖性视为仅有的主要效应就足够了。在制造第yi个原型之前，LTspice可以用作解释直流偏置等非理想特性的实用工具。

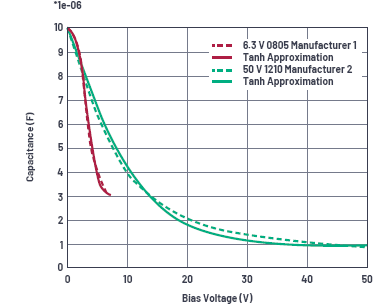
    图4.针对不同电源电压，使用Tanh模型从转换器侧仿真LT8619降压调节器的输入滤波器的干扰电流抑制