如何选择外部元件以保证稳定性和计算TIA噪声

　　利用光电二极管或其他电流输出传感器测量物理性质的精密仪器系统，常常包括跨阻放大器（TIA）和可编增益器级以便ZDCD地提高动态范围。本文通过实际例子说明实现单级可编程增益TIA以降低噪声并保持高带宽和高JD的优势与挑战。

　　跨阻放大器是所有光线测量系统的基本构建模块。许多化学分析仪器，如紫外可见（UV-VIS）或傅里叶变换红外（FT-IR）光谱仪等，要依赖光电二极管来JQ识别化学成分。这些系统必须能测量广泛的光强度范围。例如，UV-VIS光谱仪可测量不透明的样品（例如使用过的机油）或透明物质（例如乙醇）。另外，有些物质在某些波长具有很强的吸收带，而在其他波长则几乎透明。仪器设计工程师常常给信号路径增加多个可编程增益以提高动态范围。

　　光电二极管和光电二极管放大器

　　讨论光电二极管放大器之前，快速回顾一下光电二极管。当光线照射其PN结面时，光电二极管会产生电压或电流。图1显示的是等效电路。该模型表示光谱仪所用的典型器件，包括一个光线相关的电流源，它与一个大分流电阻和一个分流电容并联，该电容的容值范围是50pF以下（用于小型器件）到5000pF以上（用于超大型器件）。

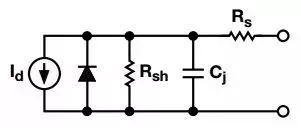
　　“图1：光电二极管模型”图1：光电二极管模型

　　图2显示了典型光电二极管的传递函数。该曲线看起来与普通二极管非常相似，但随着光电二极管接触到光线，整个曲线会上下移动。图2b是无光线存在时原点附近传递函数的特写。只要偏置电压非零，光电二极管的输出就不是零。此暗电流通常用10mV反向偏置来指定。虽然用大反向偏置操作光电二极管（光导模式）可使响应更快，但用零偏置操作光电二极管（光伏模式）可消除暗电流。实践中，即使在光伏模式下，暗电流也不会完全消失，因为放大器的输入失调电压会在光电二极管引脚上产生小误差。

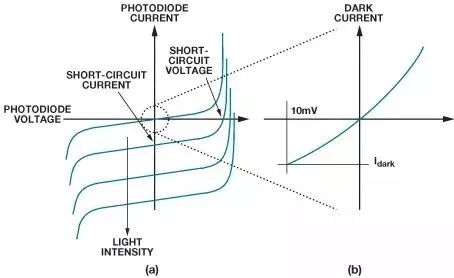
　　“图2：典型光电二极管传递函数”图2：典型光电二极管传递函数

　　在光伏模式下操作光电二极管时，跨阻放大器（TIA）可使偏置电压接近0V，同时可将光电二极管电流转换为电压。图3所示为TIA的Z基本形式。

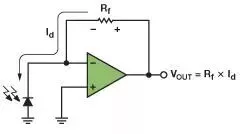
　　“图3：跨阻放大器”图3：跨阻放大器

　　直流误差源

　　对于理想运算放大器，其反相输入端处于虚地，光电二极管所有电流流经反馈电阻Rf。Rf的一端处于虚地，因此输出电压等于Rf?Id。为使这种近似计算成立，运算放大器的输入偏置电流和输入失调电压必须很小。此外，小的输入失调电压可以降低光电二极管的暗电流。放大器的一个很好的选择是AD8615，室温下其Z大漏电流为1pA，Z大失调电压为100μV。本例中，我们选择Rf=1MΩ，以便在Z大光输入条件下提供所需的输出电平。

　　不过，设计一个光电二极管放大器并不像为图3所示电路选择一个运算放大器那样简单。如果只是将Rf=1MΩ跨接在运算放大器的反馈路径上，光电二极管的分流电容会导致运算放大器振荡。为了说明这一点，表1显示了典型大面积光电二极管的Cs和Rsh。表2列出了AD8615的主要特性，其低输入偏置电流、低失调电压、低噪声和低电容特性使它非常适合精密光电二极管放大器应用。

　　选择外部元件以保证稳定性

　　一个很好的光电二极管放大器模型。该系统的开环传递函数有一个极点在28Hz，由运算放大器的开环响应引起，还有一个极点是由反馈电阻以及光电二极管的寄生电阻和电容引起。

　　“光电二极管放大器模型（a）和开环响应（b）”图4：光电二极管放大器模型（a）和开环响应（b）

　　对于我们选择的元件值，此极点出现在1kHz处，如公式1所示。

　　“”

　　注意，Rsh比Rf大两个数量级，因此公式1可简化为：

　　每个极点导致开环传递函数相移90?，总共相移180?，远低于开环幅度相移跨过0dB的频率。所示，如果缺少相位裕量几乎必然导致电路振荡。

　　为确保稳定工作，可以放一个电容与Rf并联，从而给传递函数添加一个零点。此零点可将传递函数跨过0 dB时的斜率从40 dB/十倍频程降至20 dB/十倍频程，从而产生正相位裕量。设计至少应具有45?相位裕量才能保证稳定性。相位裕量越高，响铃振荡则越小，但响应时间会延长。电容添加到开环响应中的零点在闭环响应中变成极点，因此随着电容提高，放大器的闭环响应会降低。公式2显示如何计算反馈电容以提供45?相位裕量。

　　其中，fu是运算放大器的单位增益频率。

　　Cf值决定系统能够工作的Z高实际带宽。虽然可以选择更小的电容以提供更低的相位裕量和更高的带宽，但输出可能会过度振荡。此外，所有元件都必须留有余地，以便在Z差情况下保证稳定性。本例选择Cf=4.7pF，相应的闭环带宽为34kHz，这是许多频谱系统的典型带宽。

　　图5显示了增加反馈电容后的开环频率响应。相位响应Z低点在30?以下，但这与增益变为0dB的频率相差数十倍频程，因此放大器仍将保持稳定。

　　可编程增益TIA

　　设计可编程增益光电二极管放大器的其中一种方法是使用跨阻放大器，其增益能使输出保持在线性区域内，即便对于亮度Z高的光线输入。这样，各级可编程增益放大器就能在低光照条件下增强TIA的输出，对高强度信号实现接近1的增益，如图6a所示。另一种选择是直接在TIA中实现可编程增益，消除第二级，如图6b所示。

　　(a)TIADY级后接PGA；(b)可编程增益TIA”图6：(a)TIADY级后接PGA；(b)可编程增益TIA

　　计算TIA噪声

　　跨阻放大器有三个主要噪声源：运算放大器的输入电压噪声、输入电流噪声和反馈电阻的约翰逊噪声。所有这些噪声源通常都表示为噪声密度。要将单位转换为Vrms求出噪声功率（电压噪声密度的平方），然后对频率积分。一种JQ但简单得多的方法是将噪声密度乘以等效噪声带宽（ENBW）的平方根。可以将放大器的闭环带宽建模为主要由反馈电阻Rf和补偿电容Cf决定的一阶响应。使用稳定性示例中的规格，求得闭环带宽为：

　　要将3dB带宽转换为单极点系统中的ENBW，须乘以π/2：

　　知道ENBW后，就可以求出反馈电阻造成的均方根噪声和运算放大器的电流噪声。电阻的约翰逊噪声直接出现在输出端，运算放大器的电流噪声经过反馈电阻后表现为输出电压。

　　其中，k是波尔兹曼常数，T是温度（单位K）。

　　Z后一个来源是运算放大器的电压噪声。输出噪声等于输入噪声乘以噪声增益。考虑跨阻放大器噪声增益的Z佳方式是从图7所示的反相放大器入手。

　　“图7：反相放大器噪声增益”图7：反相放大器噪声增益

　　此电路的噪声增益为：

　　“”

　　使用图4a所示的光电二极管放大器模型，噪声增益为：

　　“”

　　其中，Zf是反馈电阻和电容的并联组合，Zi是运算放大器输入电容与光电二极管的分流电容和分流电阻的并联组合。

　　此传递函数包含多个极点和零点，手工计算将非常繁琐。然而，使用上例中的值，我们可以进行粗略的近似估算。在接近DC的频率，电阻占主导地位，增益接近0dB，因为二极管的分流电阻比反馈电阻大两个数量级。随着频率提高，电容的阻抗降低，开始成为增益的主导因素。由于从运算放大器反相引脚到地的总电容远大于反馈电容Cf，因此增益开始随着频率提高而提高。幸运的是，增益不会无限提高下去，因为反馈电容和电阻形成的极点会阻止增益提高，Z终运算放大器的带宽会起作用，使增益开始滚降。

　　正如电阻噪声密度，图8的输出噪声密度转换为电压噪声Vrms的ZJQ方法是求噪声密度的平方，对整个频谱积分，然后计算平方根。然而，检查响应发现，一种简单得多的方法仅产生很小的误差。对于大多数系统，DY零点和极点出现的频率相对低于第二极点。

　　峰值噪声为：

　　注意，与fp2相比，fz1fp1出现在相对较低的频率。简单地假设输出噪声等于DC至fp2的峰值噪声（公式11得出的N2）将大大简化输出噪声所需的数学计算。

　　在这一假设下，输出噪声等于输入噪声密度乘以峰值增益，再乘以ENBW，即fp2?π/2：

　　知道所有三个噪声源的等效输出噪声后，就可以将其合并以求得系统总输出噪声。这三个噪声源彼此无关且为高斯噪声，因此可以求和方根（RSS），而不是将其相加。使用RSS合并多项时，如果一项比其他项大三个数量级左右，结果将以该项为主。

　响应清楚地表明，运算放大器的噪声带宽远大于信号带宽。额外带宽没有其他作用，只会产生噪声，因此可以在输出端添加一个低通滤波器，衰减信号带宽以外的频率上的噪声。添加一个34kHz带宽的单极点RC滤波器可将电压噪声从254μVrms至45μVrms，总噪声从256μVrms降至仅52μVrms。