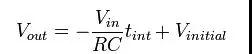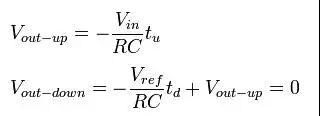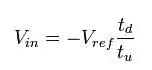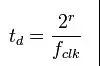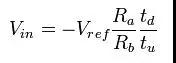一个积分型ADC是一种通过使用积分器将未知的输入电压转换成数字表示的一种模-数
转换器。在它基本的实现中,这个未知的输入电压是被施加在积分器的输入端,并且持续一个固定的时间段(所谓的上升阶段)。然后用一个已知的反向电压施加到积分器,这样持续到积分器输出归零(所谓的下降阶段)。这样,输入电压的计算结果实际是参考电压的一个函数,定时上升阶段时间和测得的下降阶段时间。下降阶段时间的测量通常是以转换器的时钟为单位,所以积分时间越长,分辨率越高。同样的,转换器的速度可以靠牺牲分辨率来获得提升。
这种类型的AD转换器可以获得高分辨率,但是通常这样做会牺牲速度。因此,这些转换器不适用于音频或信号处理的场合应用。他们通常的典型应用就是数字电压计和其他需要高测量的仪表。
========基本设计=======
基本的积分型ADC电路包含:
一个积分器、
一个选择
开关(用来选在被测电压和参考电压)、
一个定时器(用来决定对被测电压的积分时间长度和测量参考电压积分消耗时间)、
一个
比较器(用来进行过零检测)、
一个控制器、
一个放电开关(这个根据实现形式可有可无,主要用来对积分电容进行放电,与积分电容并联)。
上面的所有开关都由转换器的控制器(通常是
微处理器或专用的控制逻辑),控制器的输入包括一个时钟信号(用来测量时间)和一个比较器的输出信号(用来检测积分器的输出是否归零)
转换过程分两个阶段:上升阶段和下降阶段。在上升阶段,积分器的输入是被测电压,在下降阶段,积分器的输入是已知的参考电压。在上升阶段中,开关选择被测电压进入积分器,积分器持续一个固定的时间段进行积分,在积分电容上面积累电荷。在下降阶段,开关选择参考电压进入积分器,在这阶段测量积分器输入归零的时间。(译者:总结起来就是先定时积分,再定值反向积分,测量反向积分时间),电路如图:
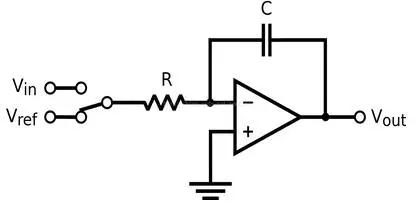
为了使积分器向相反方向积分,参考电压需要和被测电压的极性相反。在大多数情况下,如果被测电压为正,那么参考电压就为负。为了能够处理正负电压输入的情况,需要一个正向和一个负向的参考电压。具体选择哪一个参考电压取决于上升阶段积分结束后积分器的输出电压极性。也就是说,如果在上升阶段结束时,积分器输出是负,则需要接入一个负向参考电压(译者:因为接的是积分器的反向输入端),如果积分器输出是正,则需要接入一个正向参考电压。
积分器输出的基本公式如下(假设是一个恒定输入):
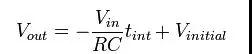
假设在每个转换过程的初始电压都是零,并且积分器在下降阶段结束时的输出电压也是零,我们就可以得到下面两个等式来表示积分器的两个阶段的输出:
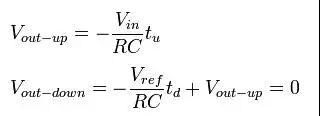
结合上面两个等式,可以解除Vin,也就是得到了被测电压的公式:
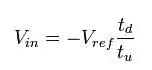
从这个公式可以看出,双斜坡积分ADC的好处之一很明显:测量结果与电路元件的值(其中的R和C)无关。然而,这并不意味着,R和C在双斜坡积分ADC中不重要(下面将解释这一问题)。
注意到在下图中,在上升阶段电压是向上升高的,在下降阶段电压是向下降低的。在实际应用中,由于比较器使用的是运放的负反馈,施加一个正向电压Vin实际会使输出下降,
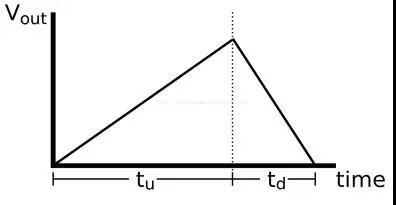
所以这里的“上”和“下”可以理解为积分电容充电的过程。
双斜坡积分型ADC的分辨率主要由下降阶段的时间长度和时间测量分辨率(例如控制器时钟的频率)来决定的(译者:也就是速度和分辨率这一对矛盾的原因)。期望的分辨率(用bits数表示) 是满量程输入时,下降时间的长度。(Vin = -Vref)
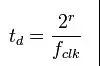
在满程输入的测量过程中,积分器输出的斜坡在上升和下降阶段是相同的(方向相反)。也就是上升和下降阶段的时间相等(),总的测量时间则为。因此,满程输入的总的测量时间是基于期望的分辨率和控制器的时钟频率的。
举个栗子:如果期望得到16bits的分辨率,控制器时钟频率是10MHz,那么测量时间计算下来就是13.1ms(也即是每秒钟76个采样)。采样时间可以靠牺牲分辨率得到改善。如果分辨率降低到10bits,那么在同样的10MHz的时钟频率下,测量时间就降低到仅为0.2ms(每秒钟4900个采样)。
========局限性=======
双斜坡积分型ADC有几个局限。对于基本的双斜坡ADC来说,靠使用更长的测量时间或更高的时钟频率来任意提高分辨率是不可能的。分辨率被以下条件所限制:
1. 积分器运放的范围。运放的轨电压限制了积分器的输出电压。长时间的积分器输入会导致输出被限制到一个值,是的任何基于下降时间的计算都没有意义。因此,应基于运放的轨电压、参考电压和期望的满程被测电压来小心地选择积分器的电阻和电容,并且长的上升时间也应满足期望的分辨率。(译者:实际就是讲积分器饱和的问题,后面的电荷平衡技术将解决这个问题)
2. 作为过零检测的比较器的准确度。宽带电路噪声限值了比较器检测积分器输出归零的能力。Goerke建议一个典型的限制是比较器分辨率1mV。
3. 积分电容的品质。尽管积分电容不需要完美的线性,但却需要时间恒定(time-invariant)。介电吸收(Dielectric absorption)会导致严重问题。(译者:个人认为此处应为介质吸收。取一个数值较大的钽电容,充电到10V左右,用一个100Ω的电阻即刻跨接在它两端,迅速放电。移去电阻,用高阻抗的
电压表观察电容两端的电压,可以看到电容又充电,几秒后达到1V左右。介质吸收现象可能与介质表面的残留极化有关。所以积分型ADC的电容应选择高质量、低介质吸收的电容,如特氟龙介质)
=======改善=======
基本双斜坡积分型ADC的设计在转换速度和分辨率方面有限制。很对针对基本设计的修改在某种程度上解决了这些问题。
针对上升阶段的改进
改进的双斜坡
基本双斜坡设计的上升阶段会将被测电压固定积分一段时间。也就是说,它终会在积分电容上建立一个不确定的电荷量。下降阶段测量这个不确定的电荷来确定被测电压。对于一个满程输入,测量时间的一半会被花费到上升阶段。对于更小的输入,相对总测量时间的一个更大比例的时间会被花费到上升阶段。所以,减少花费到上升阶段的时间可以显著降低总的测量时间。(译者:此处以图示似乎更容易说明问题。见下图)
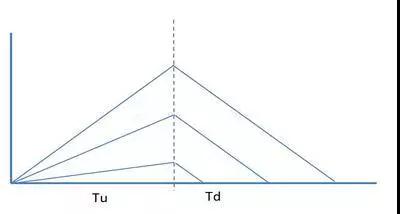
一个简单的减少上升时间的方法就是增加充电电荷的积累速度,这可以靠减少输入电阻值来实现。这依然是要积累同等数量的电荷,只是需要的时间更少。在下降阶段使用同样的算法,参考下图,则得到下面的公式:

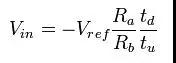
与基本双斜坡积分转换器不同,此等式与积分电阻有关。或者,更重要的是,它与两个积分电阻的比值有关。这种改进方法不能改进转换器的分辨率(因为它没有解决上面提到的分辨率的限值)。