数控振荡器的基本结构以及电路原理解析

随着数字信号处理越来越广泛的应用，数字锁相环DPLL（Digital Phase Lock Loop）在现代集成电路设计中也越来越普遍，特别是在数字信号处理器DSP和微处理器这类高性能数字电路应用中，数字锁相环更是一种必不可少的电路。与传统的模拟锁相环（Analog Phase-Locked Loop）相比，由于数字锁相环较少采用高阻值电阻、电容以及电感等非线性器件，可以采用与高速数字逻辑电路相兼容的制造工艺来设计和制造，也更加容易在数字系统中应用。
　　一个典型的数字锁相环结构如图1所示，数控振荡器DCO（Digital-Controlled Oscillator）是其中关键和的部分。数控振荡器DCO输出了可变频率的振荡波形，决定了整个锁相环的噪声性能和功耗。数字时间转换器（Time - to - DigitalConverter）输出了参考时钟和反馈来的输出时钟之间的相位差，一个数字环形滤波器（Digital LoopFilter）代替了模拟环形滤波器来控制DCO，由与参考时钟的相位差来控制DCO输出或高或低的振荡频率，输出振荡信号由负反馈送到数字时间转换器，使相位差减小，终让输出信号频率与参考时钟频率一致，即达到相位锁定。整个DCO 因此不再需要含有电容或电感，同时也减少漏电流和电源噪音的问题。
　　

　　图1 数字锁相环的基本结构
　　2 电路结构和原理
　　数控振荡器有多种实现结构，本文设计了一种完全采用静态CMOS 逻辑电路的DCO结构，该DCO基于由CMOS 反相器构成的环形振荡器，其电路结构如图2 所示。
　

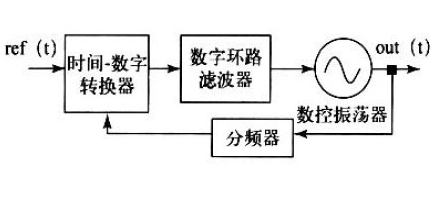
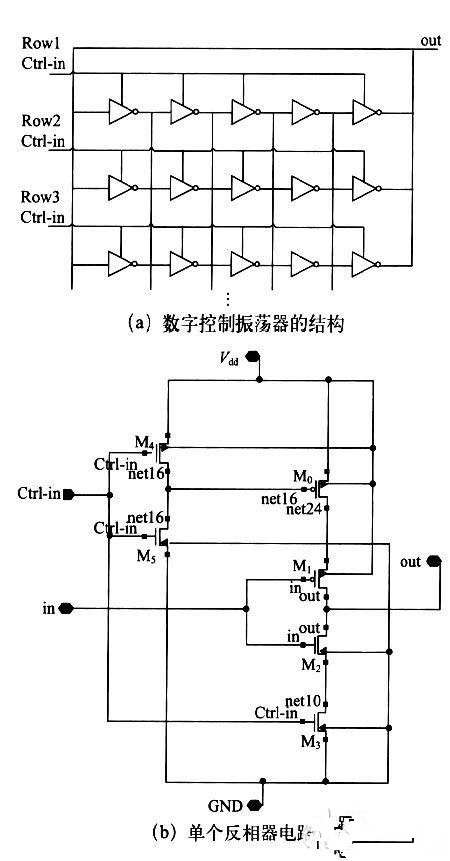
　　图2 电路结构图
　　如图2 所示，每环形振荡器均是5 个CMOS反相器串联，并构成闭环负反馈回路，每个反相器的输出也与下环形振荡器对应的反相器输出相连。根据巴克豪森准则：振荡器要产生振荡，那么环路增益必须大于等于一且总相移有360°。因此环路中进行反相的次数必须是奇数，三个以上的奇数个CMOS 反相器串联闭环回路，在一个微小的激励下都能够产生振荡。单级环形振荡器的振荡频率由反相器个数和其本征延迟决定，用n 表示反相器个数，tr 表示反相器上升沿延迟，tf 表示反相器下降沿延迟，频率可以用下式表示为：

　　反相器下降延迟t f 和上升延迟t r 根据下列公式定义，式中Rn、Rp 分别为图2（b）中反相器PMOS管M0、M1 和NMOS 管M2、M3 的等效电阻，Cout 为反相器输出电容。
　

　　设置电路中所有MOSFET的沟道长度都为90nm工艺设计规范的默认值0.1 μ m。因为在常温下N 沟道中的电子迁移率大约是P 沟道中的空穴迁移率的2~3 倍，因此设置PMOS 管的宽度Wp 是NMOS 管宽度Wn 的2 倍，使反相器中NMOS 管和PMOS 管的等效电阻近似相等，即Rn=Rp，也就使tr=tf。
　　下降延迟t r 和上升延迟t f 相等可以让环形振荡器产生对称性比较好的波形，提高振荡器的抗噪声性能。
　　每的5 个CMOS 反相器由一个高电平有效的输入信号控制，同时打开或者关闭，让DCO 中的环形振荡器逐级打开或者逐级关闭。当打开的环形振荡器级数越多，电路中的振荡电流越强，电路输出的振荡频率就越快。反之，当打开的环形振荡器级数越少，电路中的振荡电流减弱，但因为整个DCO中的环形振荡器总级数是一定的，因此整个DCO 中的等效电容并没有减少，所以输出的振荡频率就会下降。因此，该数控振荡器是通过控制打开的环形振荡器级数，数字化地控制振荡频率，在DPLL中需要一个前置的数字环形滤波器提供输入信号，控制各级振荡器的打开或关闭。
　　当所有环形振荡器都打开时，无论该DCO 中总共有多少级环形振荡器，DCO 输出的振荡波形的频率fmax 都为式（1）表示的单个环形振荡器振荡频率。输出的频率fmin 也就是当只有环形振荡器打开时的DCO 输出频率。由此分析，DCO 的增益可以如下式表示，式中N 为电路中总的环形振荡器级数：
　　

 

　　由上述分析可见，当该DCO 中具有的总的环形振荡器级数越多，可以输出的fmin 越小，KDCO 也越小，也就是每环形振荡器开关所控制的频率增减也越小，振荡器线性度也就越好。
　　3 仿真结果
　　本文基于STMicroelectronics的90nm CMOS混合信号工艺，采用Cadence Virtuoso 设计软件，使用Analog Environment 中的Spectre仿真器进行仿真。由于电路完全与数字集成电路工艺兼容，因此也可以采用诸如硬件描述语言来设计电路。
　　由32 级环形振荡器构成的数控振荡器DCO 在Cadence Virtuoso 中的仿真电路如图3 所示，在本文的仿真中，是使用直流电压作为控制DCO 各级环形振荡器打开或者关闭的输入信号。

　　图3 32级的DCO结构仿真电路图
　　电路中电源电压VDD=1.2V，所有MOSFET 均采用9 0 n m 工艺库中的标准电压晶体管S V T（Standard Vol tage Tr ansi st or ），其阈值电压为Vthn=0.3V，|Vthp|=0.3V。当32级环形振荡器逐级打开，数控振荡器输出波形的振荡频率也逐级上升，整个数控振荡器的频率调节范围如图4 所示。
　　

　　图4 DCO输出频率调节曲线
　　当32 级DCO中的18 级环形振荡器打开的时候，DCO 的相位噪声如图5 所示。相位噪声由Spectre 仿真器的pss 分析和pnoi se 分析测得。
　

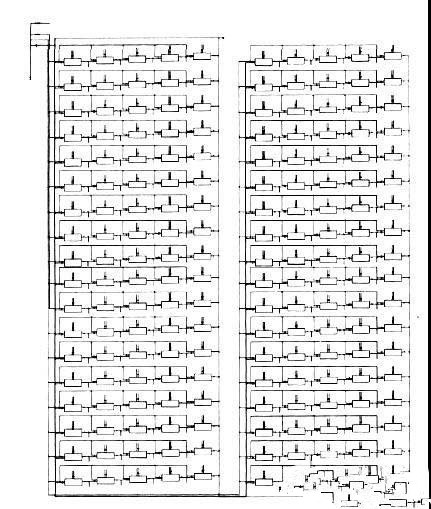
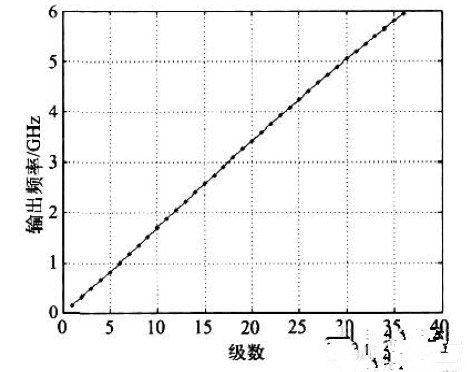
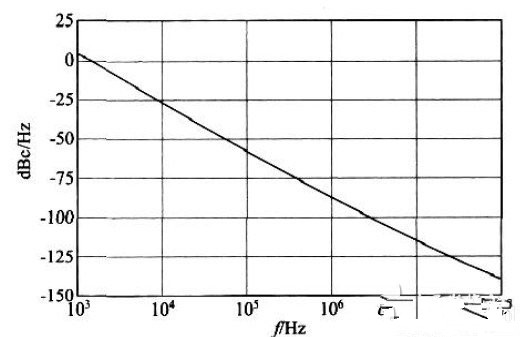
　　图5 打开18 级时的DCO相位噪声
　　该32 级数控振荡器的相位噪声和功耗如表1 所示，随着环形振荡器逐级打开，相位噪声和功耗都明显上升，这是获得高频率输出波形所付出的性能代价。先测得单个反相器的平均电流，测得各个打开的反相器平均电流均约为14 μ A，由下式可以得到电路的总功耗，式中N 为打开的环形振荡器级数。

　　为了研究环形振荡器级数对频率调节范围的影响，将数控振荡器的级数减少至18 级或12 级，再分别测试其频率调节范围。三种不同级数数控振荡器调节范围的对比如图6 所示，不同级数的数控振荡器fmax 相等，但fmin 随着数控振荡器的总级数增加而减小，且KDCO 也变小，调节线性度更好。
　

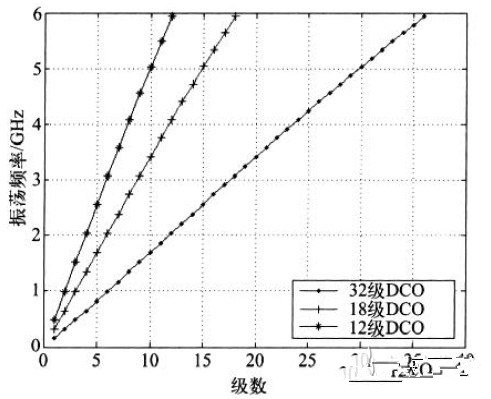
　　图6 不同级数数控振荡器的频率调节范围
　　表1 数控振荡器不同级打开时的相位噪声和功耗
　

　　进一步测试器件尺寸对数控振荡器性能的影响，当器件宽度Wn 和Wp 增加，反相器中的平均电流增加，可以输出更高的频率并减小电路中器件噪声导致的相位噪声，这对高性能电路是有意义的，但电路功耗也随之增加。对于18 级数控振荡器，保持电路中全部MOSFET 的沟道长度不变，同时增大图2（b）中的NMOS 管M2、M3 的Wn和PMOS 管M0、M1 的Wp至原尺寸的1.5 倍后测得的频率调节范围如图7 所示，全部环形振荡器共18 级打开后的DCO 功耗 及相位噪声如表2 所示。
　　表2 器件尺寸不同时测得的功耗及相位噪声
　

　　

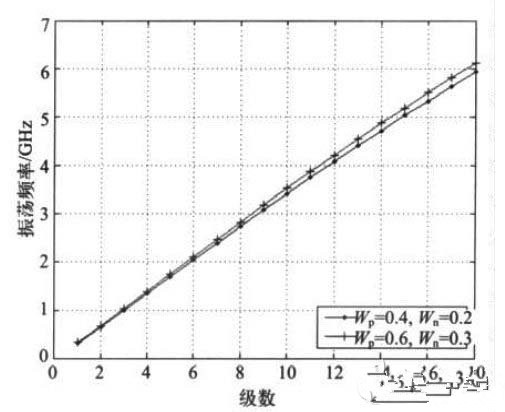
　　图7 器件尺寸不同时测得的频率调节范围对比
　　4 结论
　　该数控振荡器结构采用全静态CMOS逻辑电路来设计，获得了线性度较好的频率调节范围，在90nm混合信号工艺条件下全DCO电路功耗在3mV左右，10MHz处相位噪声低于-110 dBc/Hz，性能相比传统LC压控振荡器有过之而无不及，非常适合应用于高性能数字电路中。在用该数控振荡器结构设计DPLL 时，应进一步增加环形振荡器级数以提供线性度更好的可调输出频率范围，并需要前置数字环形滤波器提供相配合的控制信号。