基于TMS320F28335的多频段电力系统稳定器PSS4B的实现

　　摘要：随着电网的快速发展，研究具有更宽的工作频段、能够对多种振荡模式提供合适阻尼的多频段电力系统稳定器(Multiband  PSS，PSS4B)对减少电力系统低频振荡具有重大意义。本文首先分析了电力系统稳定器PSS4B的结构、性能，在实验室完成了PSS4B的硬件和软件设计，并通过动模试验对PSS4B的性能进行验证。动模试验表明所设计的PSS4B相比传统PSS在抑制低频振荡具有优越的性能，在工作区间具有良好的适应性，同时说明所设计PSS4B的有效性。

　　0 引言

　　长久以来，低频振荡严重威胁着系统的稳定运行。电力系统稳定器(Power System  Stabilizer，PSS)作为抑制低频振荡的一种措施，由于原理清晰、设计简洁、经济适用，得到了广泛的应用。国际大电网会议也将其推荐为抑制低频振荡方案。

　　不过，随着电网的逐步发展以及大量高增益快速励磁系统的投入，振荡频率越来越低，系统的振荡模式越来越复杂，给电力系统安全稳定带来了新的挑战，也对PSS提出了新的要求，抑制特定频段振荡的传统PSS局限性日益凸显。

　　多频段电力系统稳定器——PSS4B、是在PSS2B的基础上加以改进而形成的。其突出的特性在于将转速/功率信号分为低、中、高三频段，相位、增益、输出限幅及中心频率等均可独立调整，具有更宽的工作频段，能够为多种振荡模式提供合适的阻尼，提高系统的稳定性。

　　目前，国内外对于PSS4B的研究有了一些发展，但是针对PSS4B的研究大都停留在理论仿真阶段、试验应用方面的研究还比较少。PSS4B的设计实现、动模试验将对未来工程应用推广打下基础，值得进一步的探求和研究。本文对具有更宽的工作频段、能为多种模式均提供适宜阻尼的多频段稳定器(PSS4B)作了研究，涵盖了从PSS4B的设计(硬件、软件设计)到具体实现(动模试验)全过程，验证说明所设计PSS4B的有效性以及其在抑制振荡方面的优越性能。动模试验以搭建的单机无穷大系统为基础，对比不加装PSS、加装PSS2A与加装PSS4B的工况下系统的响应情况，验证了本文所设计的PSS4B样机的有效性和在抑制振荡方面的优异性能。

　　1 电力系统稳定器PSS4B模型

　　1.1 电力系统稳定器PSS4B标准模型

　　PSS4B通过在励磁系统中选取附加信号(转速偏差△ω、功率偏差△Pe)，通过相位补偿，使之产生正阻尼转矩，从而增强系统阻尼。该模型可以在更大的频域范围内提供较好的灵活性以获得更健全的调节特性，也为保证PSS在宽频域内的鲁棒性提供了更多的自由度。PSS4B的IEEE标准模型、速度传感器框图分别如图1、图2所示。

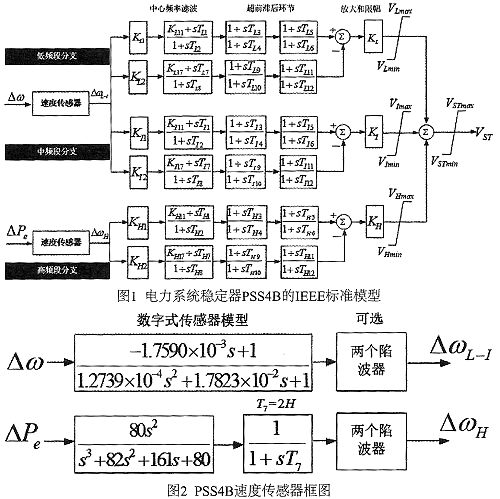
　　由图1、图2可知，PSS4B的输入信号为速度和功率偏差，通过装配2个速度传感器，一个用来从原始的转速偏差中获取中、低频段成分△ωL-I，另一个对  △Pe信号进行变换获取转速偏差的高频段成分△ωH。PSS4B的结构能够很好的兼顾低频振荡的各个频段，而且各个频段的分支相互独立，方便试验和调试。

　　1.2 电力系统稳定器PSS4B模型简化

　　除去速度传感器，PSS4B的IEEE标准模型中有60个参数需要设置，对于大多数的应用场合，一种基于六个参数即三个频段增益和三个中心频率的简化调整方法，是可以满足要求的。PSS4B的简化模型如图3所示，每个频段均简化为带通滤波器的形式，中心频率为FL/FI/FH，对应的总幅值为  KL/KI/KH。

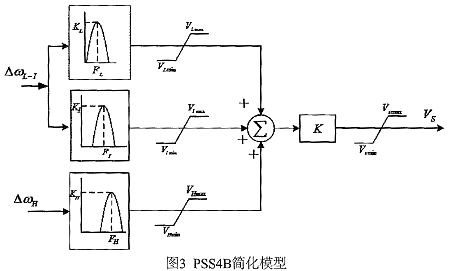
　　带通滤波器由单频段上下分支的对混合模块差分得到，为进一步简化参数，要求带通环节在中心频率处幅频响应(为1)，相频响应为0，确定中心频率之后，其他参数可以根据式(1)求出(这里以高频段分支为例，其中KH11=KH17=1)：

　　中心时间常数TH2、TH7可以直接由中心频率FH算到，而对称时间常数TH1、TH8需要借助比例系数R(R一般设为1.2)算出，式(1)保证中心频率对应的放大倍数为1，而由KH决定整个分支的增益。

　　表1给出了经简化后PSS4B所需要整定的参数，由于实际中常将单个频段内超前滞后部分上下分支设为一样，故实际需要设置的参数只有19个。

　　2 电力系统稳定器PSS4B输入信号的获取

　　作为PSS4B的输入信号，有功功率和转速的准确获取是设计重点。下面将对功率测量、转速测量的方法详细讲述。

　　2.1 功率信号测量

　　本文综合12点傅氏算法、矢量投影功率算法两种算法的特点，采用傅氏投影功率算法，在减少计算量下，保证计算。根据所用算法得到电压的有效值Vt、电流的实部Ir和Im虚部，如式(2)：

　　2.2 转速信号测量

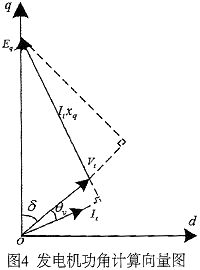
　　由于硬件获取方法偏差大，本文更推荐软件方法。如图4所示，dq坐标系中的Vt和It分别为相电压和相电流。由图可知θq=δ+θv，功率因数角θv可以通过互感器信号过零检测得到，所以只要计算出功角δ，就可以获取θq，进而对其求导得到角速度。功角δ满足式(7)：

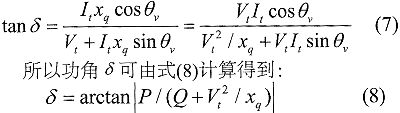
    式中自P、Q、Vt、xq分别为有功功率、无功功率、发电机机端电压、交轴同步电抗。计算得到θq后，对θq求导即可得到转速。

　　3 电力系统稳定器PSS4B的微机实现

　　3.1 PSS4B的算法

　　电力系统稳定器PSS4B的传递函数是基于S域的，不能直接微机实现，需要离散化处理。差分法主要是将微分方程用以时间为变量的时域方程表示，且只需要采集变量的时域值。本节以PSS4B传递函数的低频段分支为例，采用差分法对其离散化过程进行推导，另外两个分支的推导方法类似。

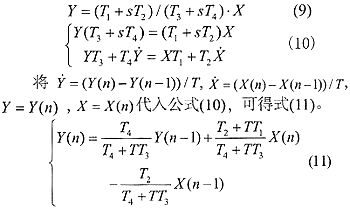
   假设某传递函数为(T1+sT2)/(T3+sT4)，输入信号为X，输出为Y，则

式(11)中，T为采样间隔，本文PSS4B程序的采样间隔取为10ms，Y(n)、X(n)和Y(n-1)、X(n-1)分别为当前输出、输入量和上输出、输入量。

    如图5所示，将上述对传递函数的离散化过程应用于PSS4B的低频段分支，可以得到离散化后的低频段分支传递函数模型，离散化模型如式(12)。

　　对于低频段的下分支，其计算公式与上面类似，这里不在赘述。据此可得终的输出信号为：

　　y(n)=(x4(n)-x40(n))·KL (13)

　　中频段和高频段分支的离散化推导方法与上述过程类似，根据得到的离散化公式，可以很方便采用C语言编程，完成PSS4B子程序的编写，实现PSS4B的算法设计。

　　3.2 电力系统稳定器PSS4B的实现

　　图6给出PSS4B输出接入到励磁控制的示意框图。根据图6给出的示意图，PSS4B的微机实现主要包括硬件设计和软件设计。

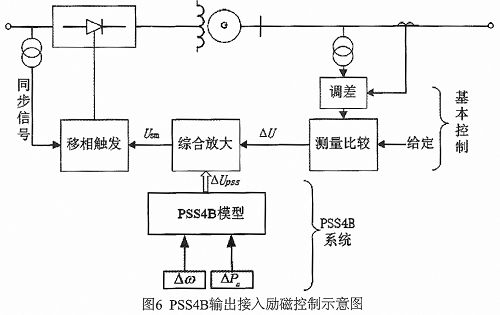
　　PSS4B硬件系统设计主要包括以下几部分：模拟信号调理电路、开关量输入/输出电路、数模转换接口设计等，主要完成数据的采集、控制信号的输出等工作。硬件系统的设计是围绕TI(Texas  Instruments)公司的32位浮点DSP—TMS320F28335主控芯片进行的。同时选取两个互为热备用的控制通道的冗余结构来保障系统的可靠性，两个控制通道的芯片都采用F28335，从模拟量的获取到控制信号的输出相互独立。

　　PSS4B的软件系统设计主要包括：交流采样算法、PSS4B主程序设计以及PSS4B微机实现等几方面的内容。软件设计的环节是电力系统稳定器  PSS4B的主程序设计：转速和功率偏差作为PSS4B的输入信号，按照本文第2部分给出的数学模型实现输入信号的获取;同时按照前文介绍的PSS4B离散化模型完成PSS4B标准模型的实现。PSS4B的输出提供给控制程序，参与励磁辅助调节，同时传递给触摸屏或上位机，方便人机互动。

　　4 电力系统稳定器PSS4B的动模试验验证

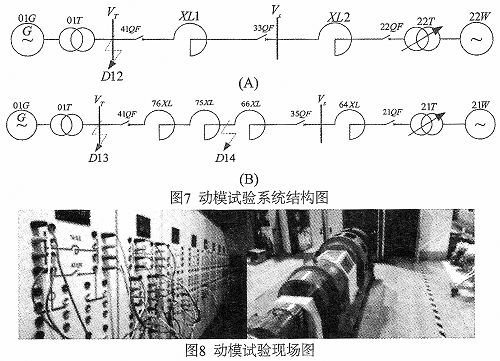
　　为验证电力系统稳定器PSS4B设计方案的有效性，对本文提出的PSS4B设计方案进行了动模试验，动模试验中搭建了两个系统(A系统和B系统)，如图7  所示，主要差别在于输电线路的长短和阻抗值不一样，用来说明电力系统稳定器PSS4B对不同振荡模式的适用性和鲁棒性。其中发电机和无穷大系统的参数如下：1号发电机参数SN=5  kVA，VN=100 V;

　　21、22号无穷大系统参数SN=100kVA，VN=800V;升压变压器(01T)参数SN=5kVA，变比为100/800。通过设置发电机机端或输电线路三相短路来模拟系统遇到的大干扰，诱发低频振荡，A系统设置了一个故障点(D12)，B系统设置了2个故障点，分别在1号升压变压器高压侧  (D13)、75XL与66XL之间(D14)，图8为动模试验的现场图。

    4.1 参数整定

    PSS优化参数的整定参考文献中的方法，依据文献方法确定的PSS4B、PSS2A优化参数如表2、表3所示。

   4.2 动模试验结果

     A系统对试验系统设置了3种不同的输出有功功率工况;B系统对试验系统分别设置了2种不同的输出有功功率工况。研究不加PSS、加装PSS2A以及加装PSS4B三种情况下的系统响应。图9和图10分别为两个系统动模试验的录波图。

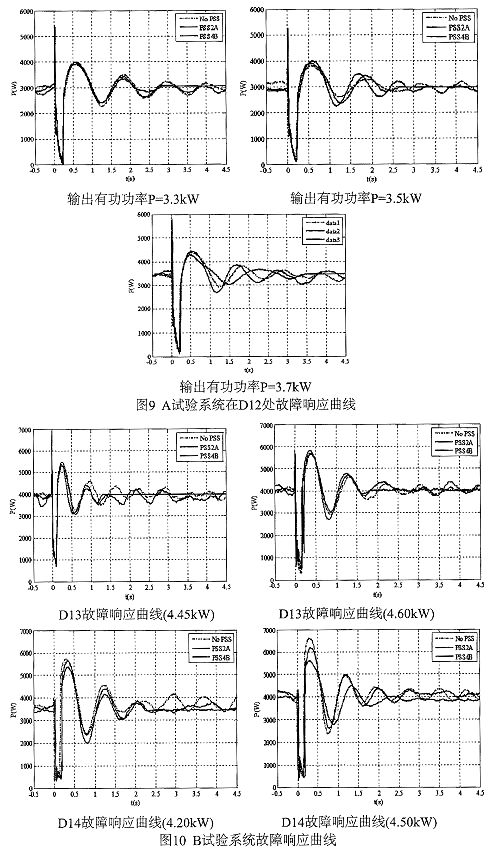
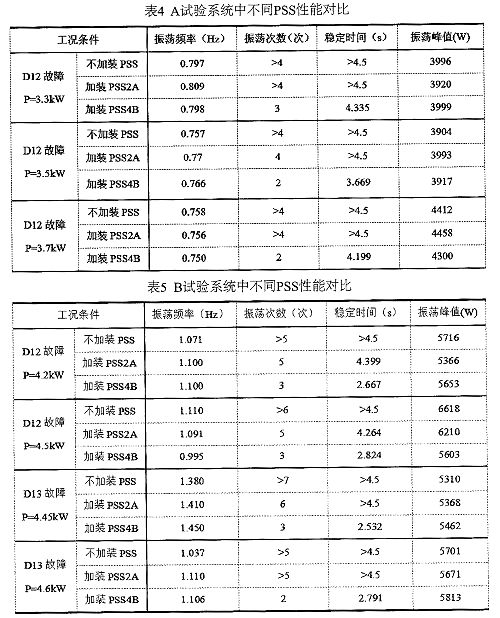
　　为了说明不同PSS在抑制低频振荡方面的性能，对A、B试验系统响应曲线的一些特征量进行了统计，如表4、表5所示。从表4、表5可以看出：A、B试验系统发生三相短路故障之后，出现了低频振荡，不加装PSS时，系统因为阻尼较小，而出现持续性振荡，在录波时间内系统未恢复稳定，振荡还有继续加剧的趋势;加装PSS2A之后，系统的振荡情况稍微有所改善，但系统并未在录波时间内稳定，只是第2～5个波头的振荡幅度有所降低，系统的低频振荡并没有得到有效抑制，同时随着功率的增大和振荡频率的降低，PSS2A抑制低频振荡的能力变弱，不能很好地适应功率变化，其适应性和鲁棒性较差;加装PSS4B之后，系统在以上三个故障点的工况中均有比较好的表现，振荡次数被削减到了2～3次，在录波时间内就恢复了稳定，系统的振荡得到了抑制，说明系统阻尼有了比较明显的加强，表现出很好的抑制低频振荡的能力，同时对于不同的工况和振荡频率PSS4B也表现出很好的适应性和鲁棒性。

　　综合以上结果分析，A、B动模系统试验表明，所设计的电力系统稳定器PSS4B能够有效抑制实际系统产生的低频振荡，甚至在加装PSS2A效果不佳的更低频段仍能发挥效用，展示了其较好的适应性，证明本文所设计的PSS4B达到了设计预期，实现了预计的效果，具有很好地工程应用价值。

　　5 结束语

　　本文研究和分析了多频段电力系统稳定器(PSS4B)的数学模型，据此完成了PSS4B的硬件和软件设计，并对所设计的PSS4B进行了动模试验。通过动模试验，验证了所设计PSS4B的有效性，以及PSS4B的优越性能，得出以下结论：

　　(1)PSS4B模型较其他传统PSS复杂，实际应用中需通过简化模型，减少待设置参数;PSS4B的工作性能与输入信号(转速、功率)测量的准确性有很大关系，采用傅氏投影功率算法计算有功功率能够减少计算量，同时保证计算;获取转速信号时，采用软件方法可以降低外界因素的影响，可信度高。

　　(2)从A、B两个动模试验系统的录波相应图可以看出，本文所设计的电力系统稳定器PSS4B对不同振荡模式都有良好的适用性和鲁棒性，同时在抑制低频振荡、增强系统阻尼、加快系统恢复稳定方面有比较明显的优势，能够有效抑制实际系统产生的低频振荡，甚至在加装PSS2A效果不佳的更低频段仍能发挥效用。本文所设计的PSS4B达到了设计预期，实现了预计的效果。

　　(3)本文的动模试验是在单机无穷大系统上进行的，考虑到实际电网为多机系统，振荡模式更加丰富，研究PSS4B在多机系统动模试验中的性能，更能体现PSS4B的特性，这也是今后研究的一个方向。

　　总之，本文对PSS4B的设计与实现作了一些探索，达到了预期目标，展现了良好的工作性能，希望对未来PSS4B的工程推广应用有一定的帮助。