犯错乃人之常情。但对于系统的模数转换器(ADC),我们能够提出什么样的要求呢?我们将回顾转换误差率(CER)测试的范围和高速ADC的分析。取决于采样速率和所需的目标限值,ADCCER测量过程可能需要数周或数月时间。为实现高置信度(CL),出现首次错误之后常常还需要进行测试(Redd,2000)。对于那些要求低转换误差率的系统,需要付出努力来详尽地予以量化。一切完成后,我们便能确定高置信度的误差率—优于10–15。许多实际高速采样系统,如电气测试与测量设备、生命系统健康监护、雷达和电子战对抗等,不能接受较高的ADC转换误差率。这些系统要在很宽的噪声频谱上寻找极其罕见或极小的信号。误报警可能会引起系统故障。因此,我们必须能够量化高速ADC转换误差率的频率和幅度。
首先,让我们理清误差率描述中的两大差异。转换误差率(CER)通常是ADC关于模拟电压采样的判断不正确的结果,因此,与转换器输入的满量程范围相比较,其相应的数字码也不正确。ADC的误码率(BER)也能描述类似的误差,但就我们的讨论而言,我们把BER定义为纯数字接收错误;如果没有这种错误,那么转换的码数据就是正确的。这种情况下,正确的ADC数字输出未能被FPGA或ASIC等下游逻辑器件正确接收到。代码出错的程度及其出现的频率就是本文余下部分要讨论的内容。仅仅阅读数据手册中的技术参数,可能难以掌握ADC转换误差。使用转换器数据手册中的单个数据,当然可以对转换误差率进行某种估计,但该数据量化的到底是什么呢?您无从判断多大的样本偏差可被视为错误,无法确定试验测量或仿真的置信度。必须将“错误”定义限定在已知出现频率所对应的幅度以内
有多种误差源会造成ADC转换错误,内部和外部均有。外部误差源包括系统电源毛刺、接地反弹、异常大的时钟抖动和可能有错的控制命令。ADC数据手册中的建议和应用笔记通常会说明避开这些外部问题的系统布局做法。ADC内部误差源主要可归因于亚稳态(Beavers,2014)或模拟域中各级之间的残余处理传递,以及数字域和物理层中的输出时序误差。ADC设计团队在器件开发过程中必须分析这些挑战。
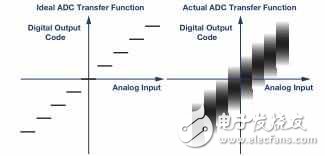
图1. 对于满量程上模拟分辨率的各个位,理想ADC样本都有单一数字输 出(左图)。实际ADC输出行为的一个例子(右图)显示了与内部和外部噪声
相关的某种模糊性。

图3.输入端开路或浮空时,理想ADC会采样输出一个中间电平失调码,如左侧直方图所示。实际ADC会有折合到输入端的噪声,其在对数尺度上应表现为高斯形状的弯曲直方图(右侧)。
ADC的积分非线性(INL)是ADC满量程输入范围内实际样本编码相对于理想输出的传递函数(Kester,2005)。ADC数据手册通常也会说明此信息并给出其曲线。与理想编码的偏差通常用某一数量的LSB来表示。下面是INL曲线示例。虽然它反映了一定量的误差,但在大部分16位或稍低分辨率的高速ADC中,INL通常只有0到3个码。它不是转换器实际误差率的主要贡献因素。
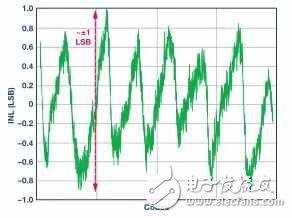
图4.INL曲线示例,在所有ADC编码上测量,与理想样本相比,误差为±1LSB或±1个码,对ADC转换误差而言基本上可忽略不计。
针对长期CER检测,测试方法可以使用非常低的ADC输入频率(相对于时钟速率而言)。在任何两个相邻样本点之间构成一条直线,正弦波斜率可近似为该直线的斜率。类似地,略高于采样速率的输入频率会混叠为低频。对于这种情况,有一个可预测的理想解决方案能让各相邻样本处于前一样本的±1个码内。输入信号频率和编码采样时钟频率必须锁定,保持可预测的相位对齐。如果此相位不是恒定值,对齐就会异相,测量数据将没有用处。因此,为了计算理想转换结果,样本(N+1)–sample(N)应相差一个码,幅度不超过1。所有ADC固有的可预测小转换误差源包括积分非线性、输入噪声、时钟抖动和量化噪声。所有这些噪声贡献都可以累加以获得差限值,若超过此限值,误差将被视为来自两个相邻转换样本。16位ADC的输出编码数是12位转换器的24或16倍。
因此,该扩展分辨率会影响用于限制转换误差率测试的编码数。在其他一切都相同时,16位ADC的限值将被12位ADC宽16倍。可使用ADC内置自测(BIST)功能并根据热噪声、时钟抖动和其他系统非线性来确定误差阈值。当超过误差限值时,可在ADC内核中标记特定样本及其对应的样本数和误差幅度。使用内部BIST的一大好处,是它将误差源界定在ADC内核本身,排除了专属于数字数据传输输出的接收位错误引起的误差。一旦明确误差阈值,便可执行涉及ADC、链路以及FPGA或ASIC的完整系统测量,以便确定全分量CER。
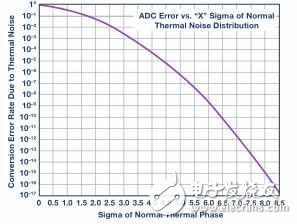
图5.ADC转换误差率与其热噪声的关系通常只能通过晶体管级电路仿真获得。上图为一个12位ADC的示例图,要实现10–15的CER,其必须能承受8Σ的热噪声。
现在看看如何计算热噪声贡献(Brannon,2003)。
SNR=20log(VSIGNAL/VNOISE)
VNOISE=VSIGNAL&TImes;10^(–SNR/20)
为得出ADC的均方根噪声,必须调整VFULLSCALE:
VNOISE=(VFULLSCALE/(2&TImes;(2)&TImes;10^(–SNR/20)
利用以下公式计算AD9625的热噪声限值,它是一款12位2.6GSPSADC,设计满量程范围(FSR)为1.1V,SNR为55,2.508MHz混叠输入频率。热噪声限值=8&TImes;VINpp×10^(SNR/20)/2√(2)=3.39mV~±12个码。
本例中,对于10–15误差限值,单单热噪声的8Σ分布就能贡献 多±12个码。这应针对ADC的折合到输入端总噪声测量进行测
试。注意:数据手册中的折合到输入端噪声可能不是基于足够 大的样本规模(用于10–15测试)而测得的。折合到输入端噪声包含 所有内部噪声源,包括热噪声。
为了明确界限以尽可能包含所有噪声源,包括测试设备,我们 使用内部BIST来测量误差幅度分布。利用AD9625的内部BIST,以
2.5GSPS运行,混叠AIN频率为80kHz,接近ADC满量程,使用标称 电源和温度条件执行CER测量,为期20天。
假设模拟电压转换为数字表示的所有ADC处理都是理想的。数 字数据仍然需要传输,并在信号链的下游FPGA或ASIC中的
下处理中接收。这的数字混乱通常由位错误或误 码率来定义。然而,ADC的数据眼图输出的综合特性可以在PCB
走线末端直接测量,并与JESD204B接收器眼罩比较,从而非常 好地了解输出质量(Farrelly,Loberg2013)1。
在1Σ内以2.6GSPS运行时,为了确立10–15的CER,10的15次方个 样本,需要让此测试连续运行4.6天。对于更大的Σ,要确立更
高的置信度,此测试需要运行更长时间2。测试需要非常稳定的 测试环境和干净的电源。被测转换器的电压源如有任何毛刺未
被抑制,将导致测量错误,测试将不得不从头再来。

图6. 利用ADC样本与理想输出码相比较的长期直方图,我们可以检测任何超出计算限值的偏差。该直方图类似于泊松分布图。
懂得单个转换器的CER之后,我们便可计算一个包含许多转换器的同步系统的误差率。许多系统工程师会问:在一个使用大量ADC的大型复杂系统中,累积ADC转换误差率将是多少?
因此,对于多信号采集系统,第二考虑事项就是确定一系列(而不是某一个)转换器的转换误差率。乍看之下,这似乎是一个令人怯步的任务。幸运的是,测得或算得单个ADC的CER之后,将此误差率外推到多个ADC并不是那么困难。这样,函数就变成基于系统所用转换器数目的概率扩张方程。
首先,求出单个转换器不发生错误的概率。它仅比1略小一点,即1减去误差率值(1–CERSINGLE)。其次,系统中有多少个ADC,便将该概率自乘多少次,即(1–CERSINGLE)#ADCs。,将1减去上述值,便可得出系统会出错的误差率。我们得到以下方程:
CERMULTIPLE=1–(1–CERSINGLE)#ADCs
考虑一个使用99个ADC,单个ADC的CER为10–15的系统。
1–CERSINGLE=0.999999999999999
CERMULTIPLE=1–(0.999999999999999)99=
9.8999999999995149000000000799095×10–14(~about10–13)
可以看出,现在的CERMULTIPLE值几乎比CERSINGLE
(10–15)大100倍。由此可以得知,含有99个ADC的系统的转换误差率大致等于单个ADC的CER乘以系统中的ADC数量。从根本上说,它高于单个ADC的转换误差率,既受单个ADC转换误差率的限制,也受系统所用转换器数量的限制。因此,我们可以得出结论:包含许多ADC的系统与单个ADC相比,总转换误差率会显著提高。
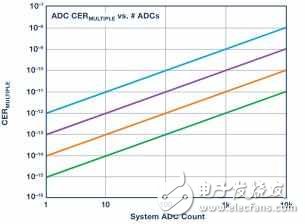
图7.使用多个转换器的系统的CER正比于单个转换器的CER乘以ADC数量。
确定ADC转换误差可能很困难,但仍是可实现的。步是确定系统中的转换误差大致有多大。然后需要确定一组适当的有界误差限值,包括预期ADC操作的非线性良性源。,特定测量算法可实现大部分或全部测试。测量结果可外推到测试界限之外,以获得额外的近似。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。