ISTREM 软件测试可靠性评估方法研究（二）

　　3.2 模型相关性的证明

　　为了进一步验证测试模型的独立性，引入皮尔逊模型来验证模型在时间上的独立性，利用统计学中皮尔逊模型计算相关度，该相关系数是判断两组数据与某一直线拟合程度的一种度量.它以用户为坐标轴，将评价的物品绘制到图上.如果两位用户的评价情况相同，那么这条直线将成为对角线.公式如下：

　　若根据实际测试情况，若根据数据计算出的皮尔逊相关系数大于0.3,则表示相关.反之，则无关，即：两两某时段失效数概率.

　　在实际的软件测试过程中，是分阶段进行的，如：静态测试.单元测试.部件测试.回归测试等阶段进行测试.在各个阶段内，统计出来的失效数是相关的.因此，根据皮尔逊相关模型计算出来的系数大于0.3 则表示相关.

　　3.3 模型的假设

　　在验证完相关性的基础之上的，在满足以下假设的前提下进行估计.以下是假设的条件：

　　3.4 模型的构造

　　模型中使用了两个参数：α是在时间 m=0 的失效率，β是对在时间段内的失效率有影响的比例常数（它是一个估计值，是对失效率造成影响的概率值），通常他的取值为较小，为0.2 或0.1.在这些估值中：m 是的观察统计时间段；s 是时间段的标志；Xk是在第 k 个时间段内发现的实际失效数；Xs-1是从第 1 到第 s-1 个时间段内发现的失效数；Xsm是从第 s 到第 m 个时间段发现的失效数；下面的似然函数为极小似然函数，为带入进行对数运算后的展开式：

　　并且Xm=Xs-1 + Xsm可以将函数展开为：

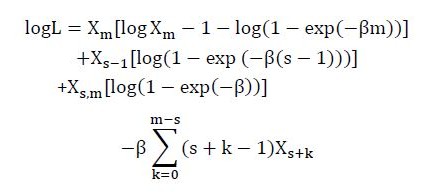
　　这个函数用来为前述方法推导估计α和β的公式.在下列公式中α和β是总体参数的估计值.

　　使用从 1 到 s‐1 时间段的累积失效统计数和 s到m（即 2≤s≤m）时间段内各段的单独失效统计数.

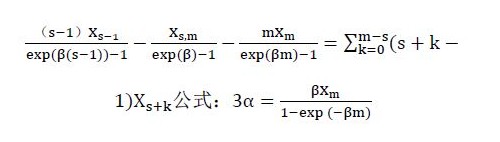
　　关于s 的值，我们使用均方差（MSE）准则能用来求得 s 的值， MSE 计算在 s≤i≤m 范围内模型预计值与实际累积的失效统计数 x（i）之间的方差和，来求出s 的值下列公式适用于上述方法：

　　这样，对于每个 s 值，用上式计算 MSE.选择使 MSE 的 s 值.结果得到对于数据集来说的三个值（β， α， s）.然后对数据运用合适的方法.

　　3.5 综合化航空电子分区操作系统的可靠性评估

　　下面以综合化航空电子分区操作系统实例进行测试评估.在ARINC653 平台中，每一个模块都是以分区的形式出现的，分区之间是相互独立的，互不干扰.它们之间分区内通信主要包括黑板.信号量.消息队列.事件等.这些应用都是该模型的一些单独而又相关的运用，它们共同组成一个综合的可靠性大纲.在此，我们只对飞控平台的燃油模块进行测试，燃油分区应用软件是机电管理分系统机电管理计算机的功能分区应用软件之一，同时也是燃油系统的重要功能组成部分，它运行于机电管理分系统的两台机电管理计算机的燃油分区中.

　　燃油分区应用软件实现对燃油系统部件的自动控制和系统状态信息的监控.显示.告警和记录功能.并且对大量的测试用例进行统计，得到以下统计结果进行平台可靠性的评估.

　　在实际测试过程中，我们还可以分别对各个模块进行可靠性评估，然后根据各个模块的评估结果对整个系统做整体评估.针对燃油平台做大量且可靠的测试， 依据我们得到的实际数据并结合ISTREM 模型进行可靠性评估.

　　下面我们先根据数据来证明我们提出模型的前提为在测试阶段之中是相关的，而测试阶段之间是无关的.然后以三种方法中的第二种为实例来行评估演示：其中 T≥s,对于方法一和方法三，s=1且 T≥1,其中 T 推荐用执行时间（编写好测试用例后，机器执行测试的时间），但也能用工作时间或日历时间：

　　使用Testbed 对基于AR I NC653 是针对航电系统的燃油模块经行测试，图1 为Testbed 的测试截图：

　　主要测试过程分成12 个阶段经行具体测试，并且对测试结果进行详细统计，得出以下数据：

　　12 次测试的故障数（12 个阶段）：100 7626 10 5 2 3 1 1 1 1 0估计出的曲线预测得到的故障数目（分30 个抽样点，这30 个抽样点随机分布在6 个测试阶段中，图2 为30 个抽样点的数据）：根据实际阶段内和阶段外的失效数，我们带入皮尔逊公式计算出段内的平均相关系数为0.423,所以可知段内相关.

　　:

图2

　　由计算的出段与段之间的相关系数为0.132,可知无关，下面的图3 可以清楚的看出段与段的无关性.

　　使用MATLAB 进行模型仿真，把统计得到的数据带入公式2.3.4 中得到α.β的值：α=0.131 ,β=0.2.

　　将α=0.131,β=0.2 带入上式得到预测如上预测数据，和分布图.

　　图4 为后整个燃油分区48 个测试阶段故障数目的累计图，这里一个阶段为时间单位.

　　依据非线性泊松概率分布的特性，可以得到：

　　则 F（0.881）=P（ r ≤0.881）=0.186 5,软件正确性大于 0.881 的可靠性为 0.9835,通过与测试标准中设定的大于0.98 的可靠性对比可知，之前求得的测试的结果，即如果软件测试的可靠性要求达到 0.98,那么该燃油分区的测试结果是可靠的.对于其他模块，可以用同样的方法进行评估，通过计算，可以对整个软件的可靠性有一个整体的评价.

　　4 结束语

　　软件的可靠性是衡量软件质量的一个重要指标.本文提出一种新的模型建立评估软件测试可靠性模型，根据实际测试统计值带入评估软件的测试可靠性.在验证和假设已知软件正确性的情况下，我们在本文中建立模型有一定的缺点，首先它不考虑测试软件在不同时间段的失效之间的相关性，这在软件测试过程中是会出现的；其次在本文中对于重复的失效测例我们不以考虑；此外使用此模型是等长的时间段较长，在以后的工作中我们会改进算法使得等待时间尽可能的变短.这些不足在以后的工作中会通过算法或者模型的改进得以解决.