分析脉冲压缩原理设计及FPGA实现

　　0 引言

　　随着现代科技的发展，对雷达的作用距离、距离分辨力等性能提出了越来越高的要求。根据雷达理论，距离分辨力取决于信号的带宽，探测距离取决于信号的时宽，所以理想的雷达信号应具有大时宽带宽积。单载频脉冲信号的时宽带宽积近似为1 ,因此作用距离与距离分辨力存在矛盾。采用脉冲压缩可以有效解决上述矛盾，这样既提高了雷达的作用距离，又保证了较高的距离分辨力。用数字方式实现的脉冲压缩具有可靠性高，灵活性好，可编程、便于应用。

　　1 脉冲压缩原理及Matlab仿真

　　1.1 线性调频信号脉冲压缩原理

　　大时宽带宽信号的实现是通过脉冲压缩滤波器实现的。这时雷达发射信号是载频按一定规律变化的宽脉冲，即具有非线性相位谱的宽脉冲。然而，脉冲压缩滤波器具有与发射信号变化规律相反的延迟频率特性，即脉冲压缩器的相频特性应该与发射信号实现相位共轭匹配。匹配滤波器的实现是通过对接收信号si（t）与匹配滤波响应h（t）求卷积得到的，即：

　　数字脉冲压缩的实现方式有两种。一是时域卷积法；二是频域FFT法。时域处理方法比较直观、简单，运算量相对较少。另外，由于FPGA等器件的迅速发展，时域卷积法得到了更大程度的应用。频域FFT法是先经过FFT的运算，再进行IFFT运算，然后得到脉压结果，其处理在本质上是与时域卷积法一样的。通常脉冲压缩用数字滤波器来实现，这时输入信号si（t）需要通过A/D转换器将其转换为数字信号si（n）。此时，脉冲压缩匹配滤波器的输出为：

　　其实现框图如图1所示。本文的设计就是按图1的原理而实现的。

　　1.2 线性调频脉冲压缩的Matlab仿真

　　线性调频信号经过匹配滤波器直接得到的脉冲压缩输出信号并不理想，主副瓣比只有13.2 dB,这在多数情况下是不能满足要求的。因为大的副瓣会在主瓣周围形成虚假目标，而且大目标的副瓣也会掩盖其邻近距离上的小目标，造成小目标丢失，所以必须降低输出信号的副瓣。常用的方法就是加权方法。如何选择加权函数，应根据应用场合的需要，依据准则在副瓣抑制、主瓣展宽、信噪比损失、副瓣衰减速度以及技术实现的难易等几个方面考虑。

　　下面，给出仿真信号模型，并在Matlab下进行仿真，以分析加权前后的影响。仿真模型：脉冲宽度为150μs,调频带宽为2 MHz,采样周期为0.1μs,加权方式为海明加权。图2给出了采用加权函数前和采用海明加权函数后的脉冲压缩波形图。

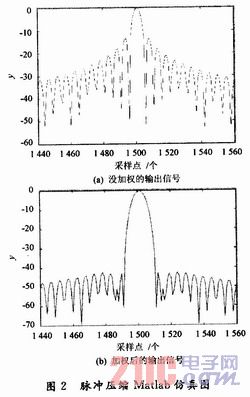
　　通过海明加权，主副瓣比大大改善，即副瓣得到了显着的抑制。虽然海明加权后带来了一定的信噪比损失，但匹配滤波器的性能得到了大大的提高。

　　2 分布式算法原理及4阶FIR滤波器的设计

　　2.1 分布式算法原理

　　分布式算法和集中式算法在设计的方法和技巧上，有着非常大的不同，原因在于分布式系统和集中式系统在系统模型和结构上有着本质的区别，集中式算法所具备的一些基本特征，在分布式算法中，已经不复存在。分布性和并发性是分布式算法的两个基本的特征。分布式系统的执行存在着许多非稳定性的因素。由于这些多方面的差异，导致分布式算法的设计和分析，较之集中式算法来讲，要复杂得多，也困难得多串行分布式算法是逐位的执行，每个时钟周期只能执行1位，速度比较慢；并行分布式算法是1个时钟周期完成1个字的运算，速度比较快；串并结合的分布式算法

　　1次可以执行多位，但是需要多个时钟周期才能完成1个字的运算，控制起来比较复杂。

　　根据分布式算法的原理得出采用FPGA实现分布式算法的硬件结构，如图3所示。

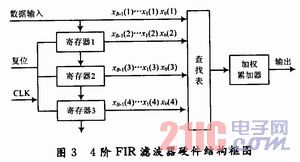
　　图3中寄存器完成数据寄存，查找表完成数据查找运算，加权累加器完成查表之后的加法。为了保证信号的完整性，即减少输出毛刺，在数据输出前用寄存器寄存一个时钟周期然后输出。

　　2.2 4阶FIR滤波器的设计

　　FIR（Finite Impulse Response）滤波器：有限长单位冲激响应滤波器，是数字信号处理系统中基本的元件，它可以在保证任意幅频特性的同时具有严格的线性相频特性，同时其单位抽样响应是有限长的，因而滤波器是稳定的系统。因此，FIR滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。

　　本文的脉冲压缩是通过并行分布式算法来实现的。从图3可以得出，4阶的FIR滤波器主要由移位寄存器、查找表和累加器组成。4为模块的滤波器阶数，那么查找表中应有24个存储单元，如果滤波器阶数过多，查找表规模随阶数的增加成指数递增，因此阶数较大时要分割查找表，分割查找表可以节省存储资源，有利于成本和资源的节约。

　　要使4阶FIR滤波器完成数据的输入、串/并转换、查表和加权累加，因为是有符号数的运算，所以要考虑累加位运算符号。FIR滤波器是线性滤波器，低阶滤波器的输出集合相加，形成一个高阶FIR滤波器的输出。为了保证信号的完整性，在程序设计时，对输入/输出数据进行了寄存处理。

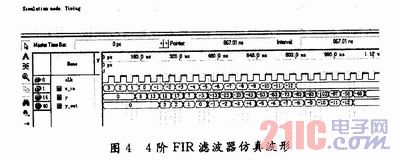
　　下面给出一个4阶的FIR滤波器设计实例。输入数据为12位有符号数，匹配滤波系数为12位有符号数，4阶FIR的仿真波形如图4所示。仿真结果与Matlab仿真结果完全一致，说明设计是完全正确的。

 

　　3 64阶匹配滤波器设计及仿真

　　由于匹配滤波器就是有限脉冲响应滤波器，具有线性特性，所以通过低阶滤波器的直接级联相加就可以实现高阶滤波器，前一个滤波器的移位数据y_out作为下一个滤波器模块信号的输入，每个滤波器模块都与4阶FIR设计相同，只需根据不同系数更改查找表中的数据。

　　在64阶匹配滤波器设计中，先用16个4阶的FIR滤波器级联成一个64阶的FIR滤波器，然后再用4个64阶的FIR滤波器组成一个64阶的匹配滤波器，即64阶的脉冲压缩滤波器。64阶脉冲压缩滤波器的逻辑设计如图5所示。

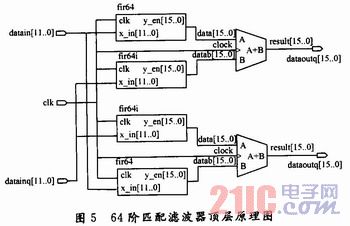
　　逻辑设计是以Altera公司的cycloneⅡ系列EP2C70为平台，在QuartusⅡ软件中利用VHDL语言和原理图进行逻辑设计，顶层为原理图，底层为VHDL文件。图5中，fir64模块为匹配滤波器实部对应的64阶滤波器，脉冲压缩加权不涉及硬件规模的增加，在实际的编程实现过程中与不加权的处理方法是完全一致的。

　　对该匹配滤波器进行波形仿真，输入为12位的有符号数据，系数为12位有符号数据，输出为16位有符号数据。由于匹配滤波器做的是64×64点的卷积，所以输出数据为64+64-1=127个。由于仿真数据较多，只给出了部分仿真结果，如图6所示。

　　4 结语

　　仿真分析表明，脉压输出的实际值与Matlab仿真值十分接近，其误差是由量化所产生的，系统具有很高的。通过仿真分析整个设计，可得出利用基于分布式算法能够大大减少数字脉冲压缩的运算量，减少FPGA的资源消耗。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点这样就会节省更多的逻辑单元，实现更多的功能。