海量地震数据准无损压缩算法设计与应用

　　摘 要： 提出了一种新的海量地震数据准无损压缩算法，并针对LWT的特点给出了率失真优化的码率分配方案。

　　在现今的电子信息技术领域，正发生着一场有长远影响的数字化革命。由于数字化的多媒体信息尤其是数字视频、音频信号的数据量特别庞大，如果不对其进行有效的压缩就难以得到实际的应用。因此，数据压缩技术已成为当今数字通信、广播、存储和多媒体娱乐中的一项关键的共性技术。

　　目前，地震数据压缩多采用基于小波变换的数据压缩技术，即通过一组小波变换，将原始数据变为相关性较小的一组系数，再对系数进行合理量化和编码以达到压缩。但野外采集的地震数据量非常大，单个文件的数据量可达数百MB至数GB.传统的小波变换方法需要将全部数据作为一个整体进行变换，运算速度慢，硬件实现复杂，内存占用大，不适合海量地震数据的实时压缩。如果对输入数据分块后再压缩，则会在边界处产生分块效应。

　　本文提出一种压缩方案，采用线扫式小波变换代替传统的小波变换，并对地震信号进行频域均衡处理。对于数据压缩技术而言，基本的要求就是要尽量降低数字化的在码事，同时仍保持一定的信号质量。不难想象，数据压缩的方法应该是很多的，但本质上不外乎上述完全可逆的冗余度压缩和实际上不可逆的嫡压缩两类。冗余度压缩常用于磁盘文件、数据通信和气象卫星云图等不允许在压缩过程中有丝毫损失的场合中，但它的压缩比通常只有几倍，远远不能满足数字视听应用的要求。在实际的数字视听设备中，差不多都采用压缩比更高但实际有损的媳压缩技术。 整个算法充分考虑了地震数据的特点，具有速度快、内存占用小、易于硬件实现的特点，能够较好地保留信号中的微弱信息，实现海量地震数据的高保真压缩。

　　1 地震数据压缩算法设计

　　本文基于LWT小波变换，设计了地震数据压缩算法。该算法包括以下五方面：（1）对原始地震信号进行预处理；（2）对预处理过的地震信号进行LWT小波变换；（3）采用频域均衡技术调整得到的小波系数；（4）对系数进行阈值处理和量化；（5）采用位平面编码方案对量化后的系数进行无损熵编码。

　　其算法流程如图1所示。采用此压缩方案，可使压缩失真较小。

15:52:08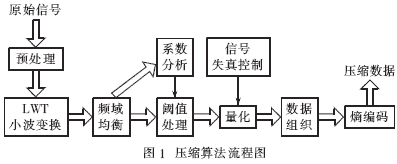

　　1.1 线扫式小波变换

　　处理二维或三维地震数据时，由于数据量极大，如果将全部数据作为一个整体进行小波变换，则需要占用很大的内存，不利于实际应用。本文采用线扫式小波变换改进算法。

　　线扫式小波变换LWT相对于传统的小波变换方法，主要在滤波顺序上作了一定的优化。做行或者列滤波并不需要多少缓存，但是在次滤波后再接着做列或者行变换时就需要较多的内存，一般要求将全部数据都存在缓存中以备后续处理。这将耗费大量的内存。

　　线扫式小波变换则是将数据源源不断地逐行输入小波滤波器，对输入的每行数据及时进行分解，分解后同时得到高、低频分量。将变换结果存在缓存器中，当积累的行数达到做列变换所需的少行数时，立即开始处理。这样存储器中始终只保存当前处理的数据，处理完之后释放存储器，这些数据将不再需要。其分解过程如图2所示。

　　数据经过线扫式小波分解后形成多个频带，所得到的小波系数与将数据作为一个整体进行小波变换所得到的小波系数完全相同，只是各个频带的数据得到的顺序不同。与将数据分块后进行小波变换的方法相比较，线扫式小波分解避免了在块边界处所造成的不连续性。对于二维地震信号，将每道的数据逐次存入列缓存，一旦列缓存中的数据达到了行方向滤波所需的数量，则对列缓存中的数据进行小波变换，并输出小波系数进行量化编码。

　　1.2 频域均衡算法

　　由于地层吸收作用，地震信号高频能量较弱，使得压缩时在高频段的相对失真较大。近年来，在地震信号的高处理与解释中，高频部分的信息也逐渐得到利用。采用频域均衡算法可有效提高压缩系统的频谱响应。

　　利用小波变换的频谱剖分性质，频域均衡算法在小波域实现。通过对不同频段的小波系数赋不同的权值以改善高频响应。如图3所示。

　　其中权值的选取一般基于频段的特

性，即通过计算子带的方差决定权值的大小。但通过实验发现，独立于小波变换尺度j的加权处理方法还是存在一定的不足。本文设计了一种与尺度相关的权值处理方法。

　　Wj=C1σmaxln（j+1）/（σj+C2）        （1）

　　其中C1、C2为常数，一般通过经验确定。j为小波变换的尺度，σmax为各尺度均方差的值，σj为尺度j的均方差。随着尺度j的增大，权值逐渐变小，这有助于平衡能量在频谱上的分布。由于地震信号中大部分信息集中在中低频段，因此式（1）在提升高频能量的同时，也适当加大了中低频段的小波系数能量。

　　1.3 率失真优化的码率分配算法

　　LWT算法在对地震数据进行变换时，小波系数是按道扫描的顺序一组一组输出的，因此需要解决如何分配各组小波系数的码率，使得在总码率一定的情况下，失真总和。为简化分析，在不考虑各组数据相互影响的情况下，任一组小波系数的码率分配必须满足式（2）：

 

　　式（2）中，D表示以码率R编码时的失真，λQ为Lagrangian常数，调整λQ的取值可使得各组系数的码率和小于或等于给定的总码率。由（2）式可得：

　　2 实验结果及压缩质量评估

　　下面是对地震信号压缩的实例。实验数据由中石油物探部门提供，采样频率为500Hz,每点数据用32位浮点数纪录。采用本文提出的LWT压缩方案进行试验，并与传统的小波压缩方案比较。

　　实验平台为Linux系统，硬件配置为P4 2.0G、256MB内存。本方案的压缩和解压速度可达10MB/s,占用的内存量可控制在20MB以内，且与地震数据文件的大小无关。图4给出了LWT压缩方案在时域和频域的失真分析。如图4（a）所示，失真随时间基本呈均匀分布，较好地保留了深层微弱信号。图4（b）、4（c）显示在信号能量集中的10~60Hz频段失真很小，60~100Hz的中高频段失真也控制在较低的范围内。

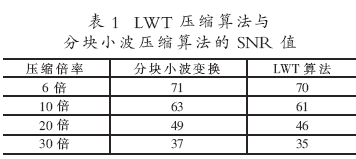
　　表1比较了LWT压缩方案与传统的小波压缩方案在不同倍率下的信噪比（SNR）。这里，传统的小波压缩方案对大数据文件采用分块处理的方式。由于LWT压缩方案不会产生分块效应，其SNR值均优于分块小波压缩。

　　针对典型地震数据信号的特点，采用频域均衡、线扫式小波变换等技术，给出了一种实用高效的压缩算法，实现了地震数据的高保真快速压缩。试验研究表明，本算法在运算速度、内存使用量和压缩失真上，性能优于传统的小波压缩方法。