摘要:通过分析三相脉宽调制( PWM) 整流器在d-q 旋转坐标系下的数学模型,设计了具有前馈解耦控制的PWM 整流器双闭环控制系统。根据系统对电流内环的控制要求设计电流比例积分( PI) 调节器,提出按闭环幅频特性峰值( Mr) 准则来确定调节器参数的方法;根据系统对电压外环的控制要求,采用模整定法来设计电压PI 调节器。对整个PWM 整流器双闭环控制系统进行仿真,仿真结果验证了PI 调节器设计的正确性。
0 引 言
PWM 整流技术在抑制谐波及无功补偿方面有很强的优势,具有网侧电流输入接近正弦,网侧功率因数可控,能量双向传输,动态响应速度快等优点。目前广泛采用的是基于电压定向的PWM 整流器。电压型PWM 整流器要控制的变量有两个,一是整流器的直流电压输出,二是整流器的输入电流,基于d-q 坐标变换的矢量控制通过对PWM 整流器有功和无功电流控制,达到控制输入电流的目的。因此,如何合理的设计控制两个变量的调节器参数以保证在电源电压波动范围内能实现良好的控制性能很重要。
本文在分析PWM 整流器工作原理和数学模型基础上,建立前馈解耦控制系统框图,提出电流环和电压环PI 调节器参数设计方法,并给出simulink 仿真结果。
1 PWM整流器工作原理及数学模型
三相PWM整流器主电路如图(1) 所示, ea , eb , ec为电源电压, ua , ub , uc 为整流器整流侧输出电压,其中整流器交流侧输入电感L 起到滤波和升高直流电压的作用,直流侧电容C 作为储能元件并起到稳压作用。三相PWM 整流器在d2q 坐标系下的数学模型为:

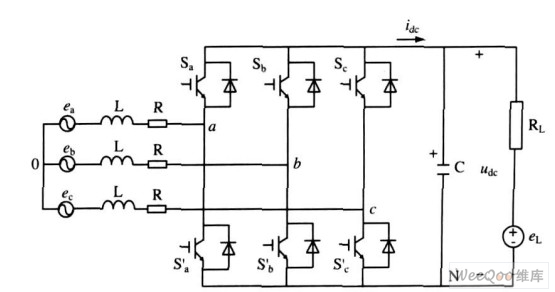
图1 PWM整流器电路结构
由上式,同步旋转坐标系中,以d 轴电源电压矢量定向(矢量图如图2 ,把对电网相电流的控制转化为对电流is在d 轴和q 轴的直流分量的控制,从而简化了PWM 整流系统控制器的设计) 的PWM整流器模型为:

式中,ω为旋转角速度; sd ,sq 为开关函数。
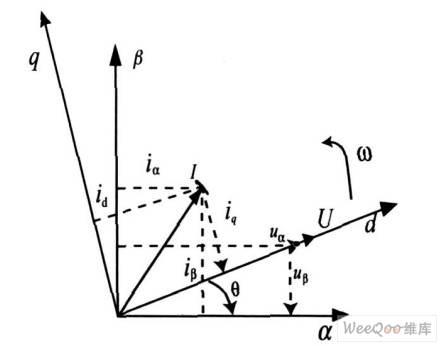
图2 d 轴电网电压定向的PWM整流器矢量图
从式(1) 数学模型看出, d-q 轴变量相互耦合,不但电压无法进行单独控制,而且给控制器的设计带来一定的困难。为此,引入id 、iq 的前馈解耦控制,对ud 、uq 进行前馈补偿,得到电流控制的两相旋转坐标系下电压指令为式(2) 。前馈解耦控制框图如图3 所示。

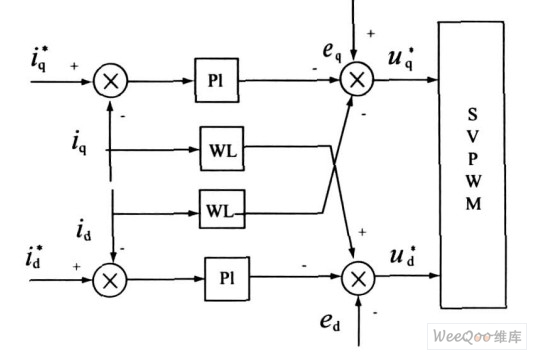
图3 前馈解耦控制框图
2 PI 调节器设计
2. 1 电流调节器
三相PWM 整流器双闭环控制中,电流环作为内环,主要作用是对电压外环输出的电流指令进行电流控制。由于典型I 型控制系统主要是提高系统的跟随性能,抗干扰能力相对较差,但交流调速系统的动态指标却以抗干扰性能为主 ,因此选用典型II 型控制系统来设计电流内环调节器,以提高系统的抗干扰能力。
从前馈解耦控制图看出 ,两个电流PI 调节器具有对称性,因此,其设计方法及参数相同,下面以iq 电流控制为例进行说明,如图4 所示。
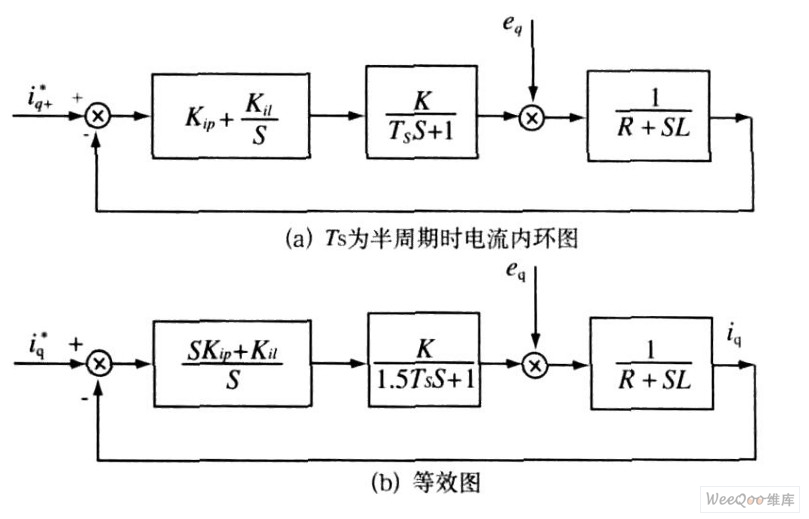
图4 电流内环结构
图4 (a) 中K 为整流器的放大倍数, Ts 为PWM开关周期的一半,如果考虑到电流信号采样的延时环节时,上图可等效为图4 ( b) 。忽略电抗器内阻时,由图4 (b) 得到电流内环开环传递函数为:

由参考文献[ 2 ]知,中频宽h 值越小,则动态降落时间ΔCmax和恢复时间tυ 越小,因而抗干扰性能越好,但h 过小又影响系统的跟随性。因此,把典型II 型系统的跟随与抗扰性能指标综合起来看, h = 5 为的选择。按Mr 准则确定典型II 型系统的参数关系,有: 。
。

由式(3) 得到:

Ts , K, L 都为已知值,则可求出PI 调节器的参数值, d轴电流i d 的控制器参数设计与此相同。
2. 2 电压PI 调节器设计
三相PWM 整流器将电压环作为外环控制,主要作用是稳定直流输出电压,提高输出直流电压,使其高于输入电压峰值,其控制框图如图5 。

式中,G1 ( S) 为电流内环调节的闭环传递函数,可近似为一阶惯性环节;G2 ( S) 为整流器的输出传递函数,其中:

Um , Im 为电源电压和输入电流幅值 。通常情况下,Tzn TP ,则 ,由此图5 (a) 可以表示为图5 (b) 。
,由此图5 (a) 可以表示为图5 (b) 。
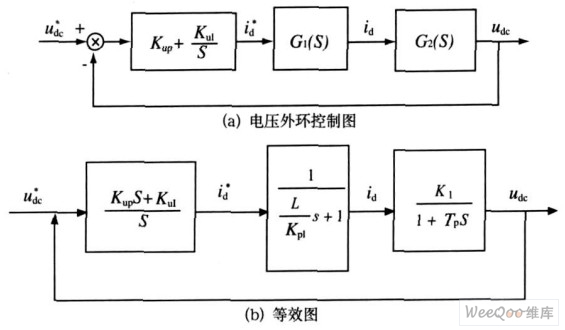
图5 电压外环结构
由图5 (b) 得到电压外环开环传递函数为:
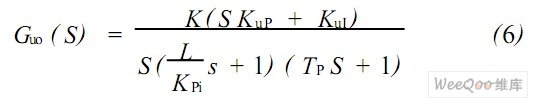
从式(6) 看出,只需以PI 调节器零极点抵消电流控制对象函数的极点即可,开环传递函数简化为:

则电压外环闭环传递函数为:

对照二阶系统的标准型则有:

根据二阶系统的模整定 ,调节器参数的模(二阶) 整定值ε= 0. 707 ,进而推出电压调节器PI参数值。
3 仿真分析
仿真参数:线电压为110 V ,开关频率为10 Hz ,交流侧滤波电抗器电感L = 4. 05 mH ,电抗器电阻R =1. 35 Ω ,直流侧滤波电容C = 3 000μF ,给定直流电压u*dc = 300 V ,直流侧负载RL = 15 Ω ,仿真时间为1 s ,在0. 6 s 时负载电流由10 A突变为20 A。
3. 1 电流环和电压环PI 调节仿真
根据系统仿真参数,取整流器放大倍数K = udc / 2= 150 ,分别代入式(4) 、(5) 得到Kip = 0. 1 , KiI = 150 。
图(6) 为电流调节器的波特图。在频率为50 Hz处,幅值变化0 . 025 dB ,相位滞后0. 51 deg ,幅值和相位的变化量都很小,证明电流内环PI 调节器参数设计合理。
根据式(4) 及所给的仿真参数,得到K1 = 5. 833 , TP =0. 0225 ,将ε= 0. 707 代入式(7) ,得到KuI = 2. 13 ,则KuP = TP KuI = 0. 048 ,图7 为电压外环PI 调节器的波特图,从图中可以看出,在50 Hz时,电压外环的带宽为12 Hz ,相角裕度γ= 42. 1°,工程上一般认为30°≤γ≤70°时,控制系统具有良好的动态性能,满足要求。
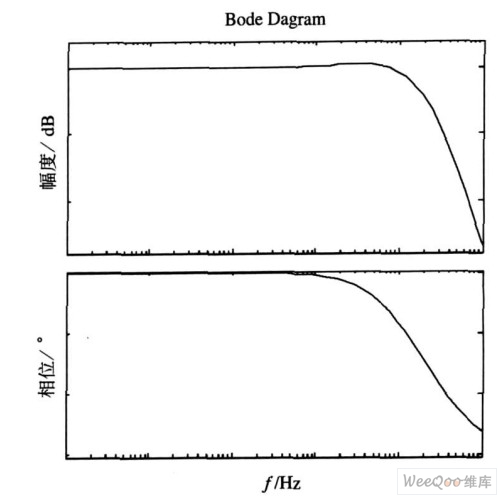
图6 电流调节器波特图
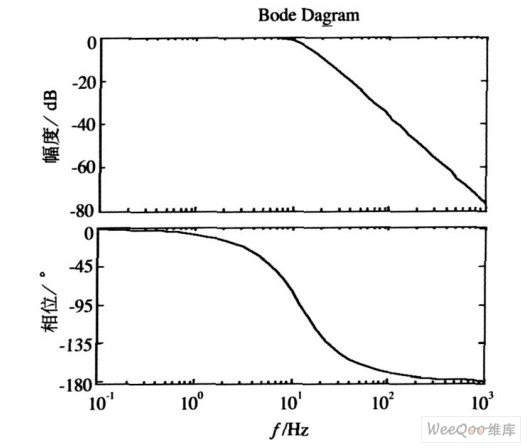
图7 电压调节器波特图
3. 2 PWM整流器的仿真
在0. 6 s时,负载电流发生突变,由图7 中得到,负载电流发生突变时超调量σ % = 0. 43 % ,超调量很小,恢复时间tv = 170 ms ,恢复时间很短,其他情况下直流电压很稳定。由图8 得到,网侧电流在负载波动后,动态响应快。图9 为网侧功率因数的仿真结果,可以看出,其功率因数达到了1 ,负载电流突变后功率因数经过瞬间的波动仍能达到1 。仿真结果验证了系统具有良好的动态和稳态性能。
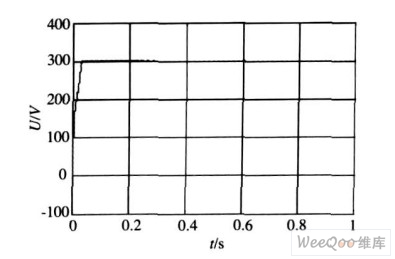
图8 直流输出电压仿真结果
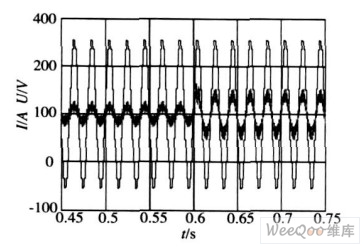
图9 网侧电压电流的仿真结果
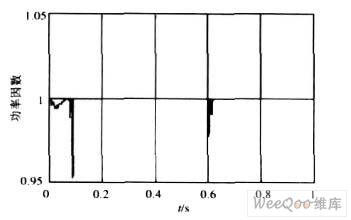
图10 网侧功率因数的仿真结果
4 结束语
本文在分析三相PWM 整流器数学模型的基础上,设计了具有前馈解耦控制的PWM 控制系统,分别根据控制要求设计了PI 调节器的参数。该设计方法简单易行,仿真结果表明系统具有良好的动态性能和稳态性能,验证了这种设计方法的优越性和正确性。
[1]. Im datasheet https://www.dzsc.com/datasheet/Im+_1064045.html.
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。