用DFT近似傅立叶变换

　　傅立叶变换对的定义如下：

　　公式假定了—个无限持续时间和带宽的连续信号。对于实际的表达式还需要在时间和频率上采样，并且对幅值进行量化。从实现的角度来讲，我们更希望在时间和频率上使用有限数量的采样。这样就产生了离散傅立叶变换（discrete Fourier Transform，DFT），其中在时间和频率上采用了Ⅳ次采样，根据：

　　如果用DFT对傅立叶频谱进行近似，就必须记住在时间和频率上采样的影响，分别是：

　　·通过在时域上的采样，可以得到采样频率为fs的周期性频谱。正如“Shannon采样定理”所陈述的：只有在x（t）的频率成份集中在一个低于奈魁斯特频率fs／2的狭窄范围内的情况下，用DFT近似傅立叶变换才是合理的。

　　·通过在频域上的采样，时间函数就变成了周期性的，也就是说DFT假定时间序列是周期性的。如果对一个信号采用N次采样DFT，没有在—个N次采样窗函数内完成整数个循环，就会产生一种称为泄漏的现象。所以，如果可能的话，并且x（t）是周期性信号，就应该选择可以覆盖整数个x（t）的周期采样频率和分析函数。

　　一种更为实用的降低泄漏的选择方案就是采用在两边逐渐衰减为0的窗函数。图1给出了一些典型窗函数的时间和频率特性^[89，129]。

　　图1 时域和频域内的窗函数

　　下面的一个示例说明窗函数的使用。

　　例 开窗操作

　　图2给出了在其采样窗口内不能完成的整数周期的正弦信号。该信号理想的傅立叶变换应该只包括两个在±ω₀处的单位脉冲函数，如图2（b）所示。图2（G）和2（d）分别给出了用不同窗函数进行DFT分析的结果。可以看到，用逻辑框函数的分析比用Hanning窗函数的分析多一些纹波。的分析也表明，用Hanning分析的主平稳宽度要大于用逻辑框函数（也就是无窗函数）分析所达到的宽度。

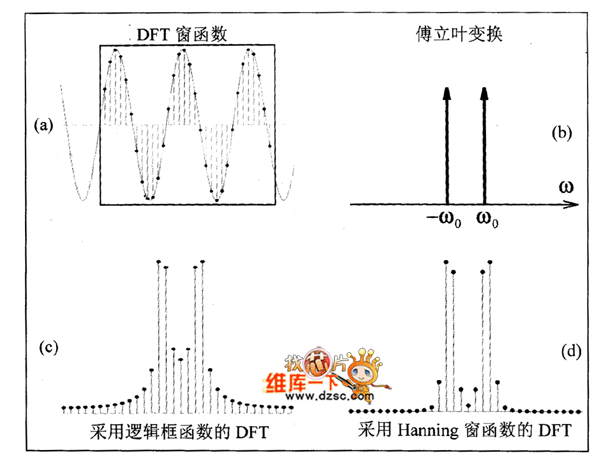
　　图2 利用窗函数分析通过DFT的周期函数

　　欢迎转载，信息来源维库电子市场网（www.dzsc.com）