LC滤波器抽头电感

　　变压器对消除不切实际的元件值是极其有用的。在“交流电路分析”中，变压比为N的变压器可以为N的实现阻抗变换。只要将其阻抗用N2乘或除，并联元件也可随意在初级或次级出现。

　　图1具体说明了如何利用电感抽头来降低谐振电容值。对图1（a）的调谐回路，首先使用一个如图1（b）所示的升压变压器，把电容C从初级转移到了次级，其电容值减小到原来的1/N2。再进一步变换得到图1（c），图中的变压器的副边合并到原边的延长部分，变成了一个自耦变压器。总电感量与抽头点电感量的比为N2。

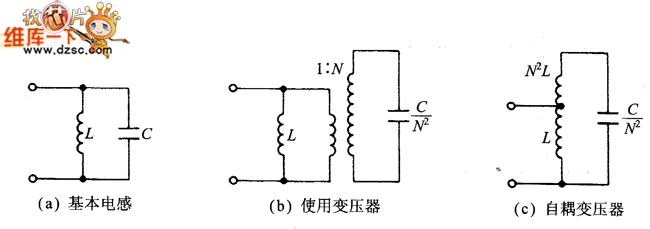
　　图1 抽头电感

　　下面以图2（a）所示的电路来说明电路变换。为了使电容值由0.354μF减小到0.027μF，总的电感按阻抗比0.354／0.027增加，得到图2（b）所示电路。其谐振频率保持不变，这是因为LC的乘积仍然是相同的。

　　通过LC椭圆函数低通滤波器进一步讨论，这种方法可以减小该滤波器中出现的并联谐振回路大电容值。图3绘出了低通滤波器的一节。为了使谐振电容变为0.1μF，总电感按因子1.055μF ／O.1μF增加，在原来的电感值处增加抽头。

　　抽头式线圈不仅可以减小谐振回路电容值，还可以对包括端接阻抗在内的整个滤波器节进行变换。抽头电感的应用范围依赖于设计者的巧妙构思。图4说明了这个技术在以往实例中的应用。图4（a）所示抽头电感可以在端接电阻不相等时仍使用巴特勒特（Bartlett）239中分定理或其他方法得到同样的结果。而且，变压器方法可得到功率传输（插入损耗）。图4（b）及图4（c）所示电路表明如何利用抽头巧妙地变换元件值。图中所有标出的各抽头电感值都是并联电感从该抽头到接地点的电感量。这样可以利用电感两边的抽头，按需要的阻抗变换系数巧妙地处理各串联支路阻抗的大小。

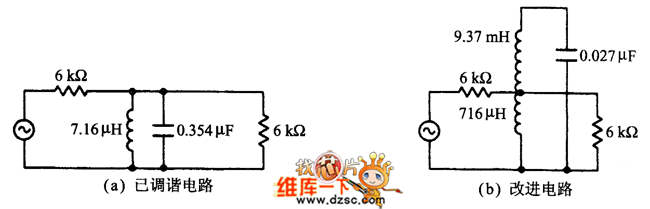
　　图2 减小谐振电容值

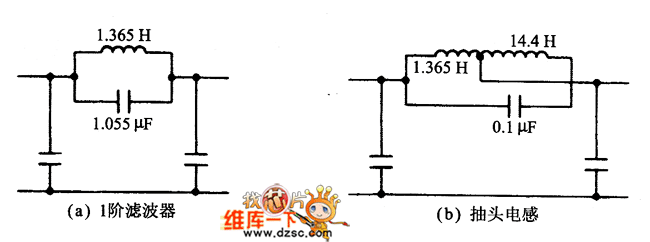
　　图3 抽头电感在椭圆函数低通滤波器中的应用

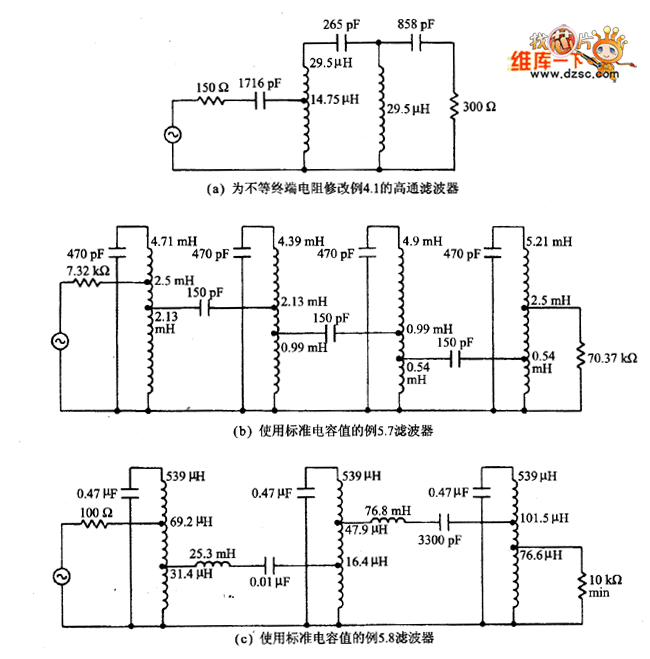
　　图4 抽头电感的应用

　　变压器或自耦变压器决非理想元件。不理想的磁场耦合将产生漏感。这漏感在高频段将引起如图5所示的杂散响应。采用接近单位匝数比，可以抑制这种效应。解决高频杂散的另一种办法是在抽头端原来的电容位置保留部分电容值作为高频旁路电容，如图6所示。

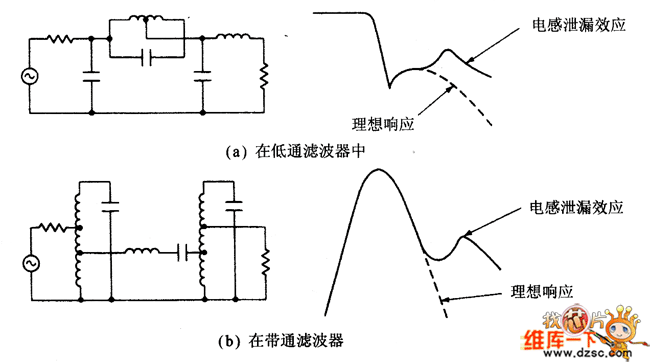
　　图5 泄露电感引起的杂散响应

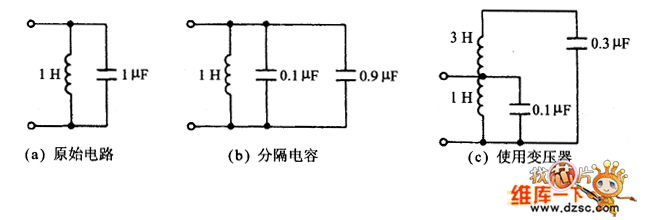
　　图6 抑制电感泄露效应