滤波器的延迟均衡

　　重点是滤波器的衰减特性,然而，如果信号是由已调波组成，则延迟特性也很重要。为了使输入信号的失真，在整个工作频率范围内，希望有固定的延迟。典型值约为6dB。由于衰减后信号在频谱上的贡献降低，衰减越大受到延迟变化（延迟失真）的影响就越小。

　　贝塞尔滤波器、等波纹误差线性相位滤波器和瞬态滤波器都有平坦的延迟。然而，幅度响应的选择性比其他类型的差。通常满足衰减指标的方法是采用巴特沃兹、切比雪大或椭圆函数型滤波器。为了同时保持延迟恒定，可以使用延迟均衡器。

　　重要的是要认识到衰减指标陡峭程度和平坦延迟之间的权衡。例如，波纹较高的切比雪夫滤波器，衰减速度越陡蛸，延迟特性特别在转折频率附近，就越不平坦。椭圆函数滤波器的延时也随着阶数、陡峭程度和纹波的增加而增加。

　　延迟均衡器网络通常至少与被均衡的滤波器有同样的阶数。所需节数取决于初始延迟曲线、被均衡部分的曲线和所需均衡的。对所需均衡器节数的一个非常粗略的估计为：

　　式中，△BW是以Hz为单位的需均衡带宽；△T是在△BW范围内以s为单位的延迟失真。

　　本文讨论的延迟均衡设计方法是图解法，而不是解析法。因此，不可能得到滤波器延迟均衡的闭式解。然而，可以使用计算机程序获得所需延迟指标的二乘逼近，这比试探法更好。

　　简单地讲，一个滤波器的延迟均衡就是设计一个网络，其延迟特性曲线与被均衡的滤波器延迟特性互补。合成的延迟特性具有所要求的平坦度。因为整个频带内延迟的变化可以导致信号的各频谱分量方式分散，虽然延迟增加了，但其影响不大。带通滤波器、延迟均衡网络的典型延迟曲线与二者合成的曲线如图所示。

　　为了用图解法均衡低通滤波器的延迟，工作频率和相应的延迟必须变换到1rad／s，以工作频率所在的曲线低端处干直流到ω＝1的频率范围。这可以用2πfh乘以延迟轴来完成，这里fh 是被均衡的频率。频率轴则除以fh，并以rad／s为单位，使fu被转换成1rad／s，其他所有的频率都对该频率进行归一化。

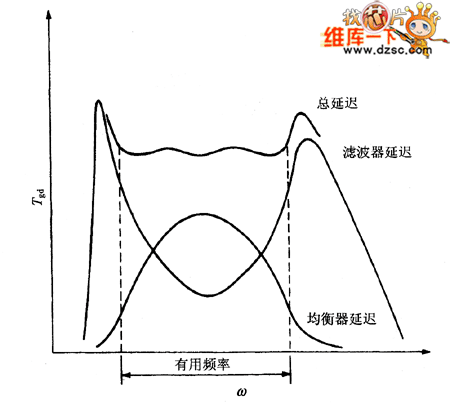
　　图 带通滤波器的延迟均衡

　　在任一情况下，从整个频带内的常数延迟中减去延迟曲线就可以得到所需均衡器的延迟特性，然后增加均衡节来逼近要得到的曲线。使用足够多的节可得到所需晦总延迟平坦度。

　　当找到与要求相匹配的特性后，可以直接使用均衡器参数来设计均衡器，然后对电路按照所需频率范围和阻抗进行去归一化。也可以先将均衡器参数进行去归一化，然后直接设计均衡器。

　　用类似于低通滤波器的方法可以对带通滤波器进行均衡。首先用2πfo乘以延迟轴，使延迟曲线归一化，其中，fo是滤波器的中心频率。频率轴除以几并以rad／s为单位，使中心频率为1rad／s，其他所有频率都对中心频率归一化。选择一条补偿曲线并使用合适的均衡节，直到满足要求为止。然后，将均衡器去归一化。