基于DSP芯片设计的一种波形发生器

　摘  要：给出了一种基于DSP芯片TMS320F240的对称规则SPWM信号生成法，较为详尽地分析了SPW M信号的谐波成分、总谐波失真度及其和载波比的关系。由于只需知道采样时刻，就可确定该采样周期内脉冲信号的开关点，因此SPWM特别适合在线计算。对生成的SPWM信号进行Fourier分析，结果表明，正弦波经过该方式调制以后，输出信号中不含有直流成分；当载波比为偶数时，输出信号中不含偶次谐波；提高载波比有利于滤除高次谐波。根据以上特点，将SPW M应用到某型制冷机减振电机的驱动上，对实测的电压和电流信号进行分析，其结果与理论分析相吻合。与采用模拟信号驱动的方式进行了比较，给出了实验结果。

　　关键词：正弦脉宽调制；谐波分析；总谐波失真度；数字信号处理；TMS320F240

引 言
　　随着电力电子的迅速发展，逆变技术已越来越多地应用到各个领域中。尤其是脉宽调制（Pulse－width modulation，PWM）技术的出现，使逆变器得到更为广泛的应用。就PWM的控制技术而言，为适应不同的应用场合和性能要求，提出了多种不同的开关器件通断控制策略^［1］。如简单的等脉宽PWM法，改变其脉冲周期可以调频，改变占空比可以调压；其缺点是输出电压中除基波外，还包含较大的谐波分量。正弦脉宽调制（Sine PWM，SPWM）法是为了克服等脉宽PWM法的缺点而发展起来的。
　　对于实时计算的PWM控制方法常常需要建立数学模型，较为常用的是采样型的SPWM法。文［2］指出，在对正弦波进行调制时，采用三角波作为载波比用锯齿波产生更少的谐波分量，自然采样SPWM法就是通过正弦波与三角波的比较来决定开关点的位置，原理简单易于用模拟电路实现。由于其开关模式不能用显式表达，难以用微机实现实时控制，因此发展了规则采样法。
　　本文给出了一种基于DSP的对称规则SPWM生成法，在建立规则采样法数学模型的基础上，分析输出波形的谐波成分，进而讨论谐波抑制的策略；然后，将SPWM法应用到某型制冷机减振电机的驱动上，并与采用模拟驱动的方式进行了实验比较，给出了实验结果。
1　对称规则SPWM的生成
　　当使用正弦波调制时，已经证明，在交流电机（如感应和直流无刷电机）的相电流中，对称的PWM信号比非对称的PWM信号引起的谐波失真更小^［2］。
　　这里给出使用TI公司的DSP芯片TMS320F240产生PWM信号的原理：为了产生PWM信号，由单独的定时器产生载波周期。当前需调制的数值与的调制数值相减，其差作为比较对象，不断地与定时器计数器的值进行比较。当两个值匹配时，相关的输出就发生跳变（从低到高或从高到低）。这样就产生了输出脉冲，它的开启（或关闭）时间与被调制的数值成正比，改变调制数值，相关引脚上输出的脉冲信号的宽度也随之改变。图1给出了对称规则PWM波形生成的原理。

2　数学模型及谐波分析
　　设正弦调制波为u_s（t）＝Asin（2πft），其中，A为正弦波幅值，f为频率，正弦波周期T＝1／f。为提高输出信号基波的值，应尽量采用大的调制深度M^［3］，这里假设M＝1。设PWM信号的幅值为E，载波比N为大于1的整数。在一个正弦波周期内，共有N个PWM脉冲，对于第n个脉冲而言：采样时刻为T（n－ 1）／N，采样值为Asin（2π（n－1）／N），由于脉冲宽度与采样值成比例及调制深度M＝1，所以第n个脉冲的宽度

设第n个脉冲的两次跳变时刻分别为t_Ln，t_Rn（如图1示），则

　　由式（2，3）可知，在对称规则采样的情况下，只要知道采样时刻n，就可以确定出这个采样周期内脉冲信号的开关点。　　
    图2表示一个周期内正弦波调制后的PWM输出波形，对它进行Fourier变换，可以得到

    考虑到上式第二项符号内的数小于0，因此

    上式第二项中，作变量代换，令n＝i＋N／2，得到

    ②若N为奇数
　　类似的，将式（6）中的u（t）按其正负分两段求和，并作变量代换，亦可得a₀＝0。
　　由①，②可见，在对称规则采样情况下，不论载波比N为奇数还是偶数，调制信号中均不含直流分量，即a₀＝0。
　　（2）k≠0时，积分式（5），并对N作奇偶分开讨论，得到如下的统一表达式

　　①若N为偶数，如前所述将求和分成两部分，并作变量代换，得到

显然，k为偶数时，a_k＝0，k为奇数时


　　②当N为奇数时，虽然也可将求和分成两部分并作变量代换，但由于采样值不像N为偶数时那样具有对称性，故无前面的简洁表达式。
    总谐波失真度

写成式（16）的目的是，避免在计算THD时，对无穷多项求和。
　　由前面的分析可知，对称规则采样SPWM信号不含直流成分，并且当载波比N为偶数时，SPWM信号中不含偶次谐波。
　　表1为输出电压频谱分布，分别对应于N＝19，20，49和50四种情况。由表可知，对称规则采样SPWM信号的谐波均分布在载波频率的整数倍附近。仿真计算表明：载波比N分别为奇数和偶数时，各自的谐波成分大致相当，如，N＝49时，谐波主要集中在46，48，50，52四个波次上；N＝50时，谐波主要集中在47，49，51，53四个波次上。
　　谐波成分与载波频率密切相关，如果提高SPWM的载波频率，则输出信号的主要谐波也会分布在较高的频率段。这样，在逆变器驱动交流电机时，电机的漏抗将会滤掉逆变器输出电压的高次谐波，而使逆变器的输出电流呈现较好的特性。

    虽然提高载波频率可以消除逆变器的低次谐波，减小电机的谐波损耗，但这也会使逆变器的开关损耗大幅度增加。为协调二者的矛盾，一般认为在中小功率的IGBT逆变器中，SPWM的载波频率取3 kHz左右为宜^［5］。
    由式（16）知，总谐波失真度THD与一个正弦波周期内PWM信号的能量及基波能量（|a₁|²）有关。图3分别表示一个周期内PWM信号的能量、基波信号的能量及总谐波失真度THD与N的关系。

图3（a，b）中实线和虚线分别表示N为奇数和偶数时的变化规律。当N＝20时，THD值与稳态值相比，误差在5％以内。因此，可以认为，当N＞20时，总谐波失真度即与N无关。图3（c）中，N为较小的偶数时，THD也较小，这是由于相对而言，此时PWM信号的能量值更小（图3（a）中的虚线）。
3　实验系统及结果分析
　　本文给出了一个对称规则采样SPWM在某型制冷机减振控制中的应用实例，以验证前面分析的有效性。该减振控制系统方案以TMS320F240控制器为器件。该控制器是专门为电机控制系统设计生产的芯片，具有强大的数据处理能力和丰富的片内外设模块，特别是片内双通道16路10位A／D转换模块和12路比较／PWM输出模块，可以直接对测量信号进行采样转换，并直接用PWM信号经过驱动电路控制电机，大大减少外围电路的设计。
　　本文制冷机的工作频率为40 Hz，振动主要体现在该频率上。减振器（直线往复电机）的工作频率也是40 Hz，只是它的振幅和相位（相对制冷机的压缩机和膨胀机的相位）根据具体的运行状况作自动调节。
　　考虑到TMS320F240的工作主频以及控制程序的复杂度，本文采用1 000 Hz的采样频率，即载波比N＝25，电源电压5 V。在此工作条件下，使制冷机的振动量减至原来的1／10以下的指标已经能够达到。具体的减振效果，限于篇幅，这里不再给出曲线。同时，本文也做了通过模拟功放对电机进行减振驱动的实验。在两种情况下，电机中的电流（决定产生的振动力）及的减振效果相当。但是后者带来的不利因素是：增加了D／A转化部分，如果是多路D／A，则电路更为复杂；引入了模拟功放，尤其是模拟功放本身的功耗较大，必须考虑散热问题。在使用SPWM控制时就没有这个问题。
　　图4（a）为实测的直线电机的电压、电流波形，图4（b）是对应的FFT分析结果（已经归一化）。由图可见，电压的高次谐波频率较高，大多位于载波频率的整数倍及其周围。从电流的谐波成分看，谐波主要集中在载波频率附近，而更高的频率则被线圈电感滤除，总的谐波成分低于基波成分的3％。
4　结 论
　　本文给出了一种基于DSP的易于实时计算的对称规则SPWM信号生成法，在建立其数学模型的基础上，较为详细地分析了信号的谐波成分。用这种方法生成的PWM信号，不含有直流成分；载波比为偶数时，输出信号中不含偶次谐波；当提高载波比时，有利于滤除高次谐波。

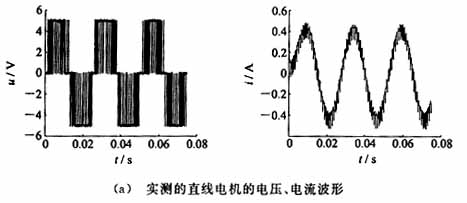
　　将对称规则SPWM应用到某型制冷机减振电机的驱动上，分析实际的电压电流信号，通过与直接模拟驱动方式比较的结果可以看出，采用SPWM控制具有电路简洁、高效节能等优点，且总的谐波含量很低。

  

参考文献:

[1]. TMS320F240 datasheet https://www.dzsc.com/datasheet/TMS320F240_309662.html.
[2]. Pulse datasheet https://www.dzsc.com/datasheet/Pulse_1195545.html.