基于16位定点DSP的并行乘法器的设计

　　摘要：设计了一种用于16位定点DSP中的片内乘法器。该乘法器采用了改进型Booth算法，
使用CSA构成的乘法器阵列，并采用跳跃进位加法器实现进位传递，该设计具有可扩展性，并提出了更高位扩展时应改进型方向。设计时综合考虑了高性能定点DSP对乘法器在面积和速度上的要求，具有极其规整的布局布线。
　　关键词： 改进型Booth编码；部分积产生器；阵列乘法器

1 引言
　　大多数先进的数字系统为实现高速算术运算都包含有硬件乘法器，例如许多高速单片机微控制器中的算逻运算都使用了硬件并行乘法器。目前广泛应用的DSP芯片内核中，通常都有可单周期完成的片内硬件乘法器，以实现某些复杂算法如滤波以及实时处理等。通常乘法器处于关键延时路径上，因此乘法器的速度对整个芯片以及系统性能有重要影响。按结构可分为串行乘法器和并行乘法器，串行乘法器面积和功耗，但是运算速度也慢，因此高速数字应用系统通常会采用并行乘法器。并行乘法器有三个主要部分[1]：部分积产生器、加法阵列块和进位加法器。部分积产生器的功能是根据输入的操作数产生部分积；加法阵列块完成对部分积的归约，是将所有的部分积相加产生2n位的结果；进位加法器是为了生成终结果。
　　本文将讨论一种用于16位定点DSP芯片的并行乘法器的设计。总的来说，对快速乘法器性能的改进，设计时不外从三个方面来考虑：减少部分积的数目，比如采用改进的Booth算法；对部分积归约，比如采用Wallace树形结构；减少进位传递时间。文中从芯片制造的角度综合衡量芯片成本、可靠性及性能后，对于部分积产生器采用改进型BoothII算法设计；加法阵列块直接用CSA阵列乘法将部分积相加生成进位项和伪和项；采用跳跃进位加法器将进位与伪和相加，产生终结果。版图实现采用静态CMOS 工艺，加法单元主要采用CMOS传输门实现。
2 计算公式
　　Booth算法适用于补码表示的乘法运算。16×16位整数AS 、BS乘积PS的计算公式[2]如下
(基2的表示)
, （b-1=0）， (基4的表示) (1)
式中，A表示被乘数；B表示乘数；P表示乘积；下标S代表补码整数；下标O代表无符号数。
　　部分积 ， n = 0,1,…7。
对于16位无符号数AO、BO的乘积，PO的计算公式为
(基2的表示)
, （b16=b17=0） (基4的表示) (2)
部分积 ， n = 0,1,…,8 ，其中b16= b17= 0，b-1= 0。
　　显然，采用基4算法比采用基2算法的部分积项简化了近一半；对于16位有符号整数的乘法，有8个部分积项，而16位无符号数的乘法，则有9个部分积项。将式(1)和式(2)统一起来，可以认为16位乘法有9个部分积，一个部分积PP8的取值为
PP8 = 0 整数乘法
A×b15×216 无符号数乘法
　　对于基更高的Booth编码，例如基8也是可以实现的，不过需要额外的加法器进行被乘数的3倍和5倍的计算，控制电路更复杂，简化部分积项的优点反而不明显。本设计中不采用。
3 逻辑设计及其设计实现
　　图1描述了该16位并行乘法器的整体结构有三个主要部分：部分积产生器、加法阵列块和进位加法器。下面详细讨论各部分的逻辑设计及实现。

图1 并行乘法器的体系结构

3．1 改进型基4 Booth编码器
　　Booth编码逻辑设计的实质，就是将部分积表达式中的系数值，编码后用逻辑表达式来描述，然后进行逻辑实现。根据基4表示的乘法计算公式可以看出，基4 的Booth编码的优点就是只有5种系数的部分积项，即0，1，2，-1，-2，也就意味着编码逻辑只需要3位，即1个符号位和2个数值编码位。本设计中采用改进型Booth编码如表1所示。根据编码表可以得出编码信号的逻辑表达式如下
NEG2n=b2n+1；B12n =b2n ^ b2n-1；

为产生所有部分积的系数，设计中采用9个Booth编码器，即Booth0，Booth1，…，Booth8。编码信号产生逻辑如图2所示，以b2n+1 、 b2n 、b2n-1为输入，3个编码信号为输出。对PP0来说，因为b-1=0，所以输入信号变为2个，因此Booth0编码结构可以简化。Boothi（i= 1，2，…，7）编码原理相同，考虑负载能力的不同，实现时用了不同结构。因为部分积PP8的作用是为了考虑有符号数和无符号数的乘法，Booth8的编码实现逻辑采用B116=b15 & SXM，B216=0，NEG=0；SXM=0时完成符号数乘法运算，SXM=1时为无符号数乘法运算。Booth编码的输出全为互补的信号，这是产生部分积逻辑的需要。

(a) Booth0 的逻辑结构

(b) Booth1和Booth i (i=2,…,7)的两种逻辑结构
图2 Booth编码逻辑实现
3．2 部分积产生器
　　首先考虑各编码数字对应的产生部分积的操作：0，作为部分积；+1，被乘数作为部分积；+2，被乘数左移一位作为部分积；-1，被乘数的补码作为部分积； -2，被乘数左移一位后的补码作为部分积。9个Booth编码器可以产生PPn（n = 0,1,…,8）等9个部分积，关于部分积的产生有不同的逻辑，本设计采用
逻辑实现如图3所示，PPi ( i = 0,1 )和PPi（i=2,…8）采用了不同结构。所产生的部分积是有
符号数，在部分积进入阵列乘法器进行归约加法之前，需要进行符号扩展，使上面逻辑式中的输入

(a) PPi 的逻辑结构 （i=0,1） (b)PPi的逻辑结构( i≠ 0或1)
图3部分积产生逻辑实现
　　信号为被乘数符号扩展位，就能很容易地实现符号扩展，大大减少了符号扩展的耗费。而对有符号数来说，在NEG2n=1时，还要与NEG2n相加，才能完成对结果的求补操作，这一操作在乘法阵列中实现。
3．3 阵列乘法器
　　当部分积PPn产生之后，将它们相加就得到乘法操作的结果[3]。布线版图规则的相加就是简单的阵列乘法器的结构，即P=（…(（（PP0+PP1）+ PP2）+ PP3) +…）+PP8 ，n个部分积需要n-1行全加器。采用3．2节的保留进位加法器CSA，即进位信号不传递给本次加法的高位，而在下次加法时传递到高位的输入端，可避免本级加法器内的进位延时。而只有到高16位字结果计算时，才将前面乘法阵列产生的伪和与进位信号相加，得到真正结果。乘法阵列采用Booth算法，原理框图如图4。每次加法可以得出低2位结果，即部分积的相加与低16位结果的产生是并行的，高位结果由一个16位的快速进位传递加法器CPA完成。

图4 16位阵列乘法器原理框图

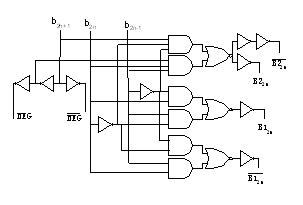
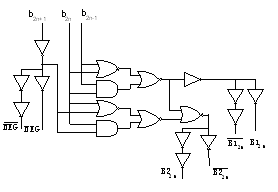
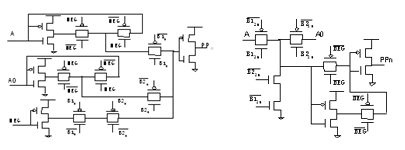
　　本设计的乘法运算是针对无符号数和有符号整数两类操作数。设计实现中，为了防止在相乘时被乘数左移可能产生的溢出，在整数运算时对其高位补两个符号位，无符号数运算时高位补两个0，形成了18位的补码表示的数据（a17a16a15,…, a0），设计实现逻辑采用a17 = a16 = & a15。
　　根据基4的Booth算法，共有9个部分积，每个为18位，所以可用8个18位全加器来完成乘法运算。图5显示了用CSA实现的乘法阵列。从图中可以看出，延迟主要由部分积(PP0, PP1)产生电路、FA以及FA0单元、进位传递加法器的延迟构成，若要求更高的运算速度，要从减少这些电路的延迟来考虑。前面已经提到的同样功能电路实现结构不同，也是基于延时及功耗考虑的结果。
3．4 进位传递加法器
　　快速进位传递加法器（CPA）是为了实现伪和与进位相加以得到终结果，除了优化设计其中全加器单元的电路结构，为进一步减少进位延迟，采用分段进位链的结构，对16位的CPA采用等

　　长分段的跳跃进位加法器来实现，分为4段，每段4位，段内以行波进位实现，如图6(a)。假设分段数为n，每段中k位，则第i段中位的进位逻辑表达式为 ，具体实现如图6（b）。

图6 跳跃进位链的逻辑实现
4 结论
　　本文设计的16位定点乘法器，版图采用上华的0.6μm CMOS工艺实现，主要模块采用静态CMOS完成，加法单元主要采用CMOS传输门实现。作为性能为20MIPS的数字电机控制DSP芯片产品的片内集成乘法器，可实现单周期乘法运算。该设计实现结构简单，设计时综合考虑了速度、面积和功耗指标，易于扩展。为扩展到更高位数的乘法器并保证其运算性能，设计实现时可考虑对处于关键路径上的单元进行改进，如对全加器单元进行优化设计；采用Wallace树形乘法阵列对部分积归约；减少高位字的进位传递时间，如 CPA实现时选取优化分组的跳跃进位加法器或者改用先行进位加法器等。

  

参考文献:

[1]. b15 datasheet https://www.dzsc.com/datasheet/b15_1826251.html.
[2]. a15 datasheet https://www.dzsc.com/datasheet/a15_1244519.html.