数字控制振荡器

概述

　　在实际的通信系统中，携带数字信息的信号通常是由某种类型的载波调制方式发送的，传送信号的带宽限制在以载波为中心的一个频段上，如双边带调制，或在邻近载波的频段上，如单边带调制。无论何种调制方式，在发送端均需要一个高频载波将信息调制上去，以减小信号衰落，相干解调时在接收端也需要一个与发送端同频同相的高频载波将信息从高频上解调下来。为了产生这个高频载波，在数字电路中是采用数控振荡器(NCO)，也称为直接数字频率合成器〔DDS)，它的输出频率和相位可以受人为控制，从而满足各种需要。

　　实时计算法的正弦波样本以实时计算产生，该方法因其计算需要耗费很多时间，因而只能产生较低频率的正弦波，而且存在计算精度与计算时间的矛盾。由于在需要产生高速的正交信号时，实时计算法将无法实现。因此，在实际应用中一般采用最有效、最简单的查表法，即事先根据各个NCO正弦波的相位计算好相位的正弦值，并按相位作为地址信息存储该相位的正弦值数据。

组成

　　数控振荡器一般由基准时钟(fclk)、相位字寄存器、相位累加器以及幅度/相位转换电路等部分组成。

　　1.相位累加器对输入频率控制字M不断累加，得到以该频率字为步进的数字相位。

　　2.函数发生模块，对当前相位进行对应幅度转换后，可以输出任意函数的波形。

　　函数发生模块最直接的实现方法是只读存储器查找表(ROM LUT)法，将正、余弦波形的抽样存放在ROM中，并通过一个DAC周期地进行输出，从而产生输出波形。如输出信号幅度位数为a，相位地址位数n所需查找表的大小为a×2n。结合上文结论可知，频率分辨率越高，所需要的ROM越大，和n为指数增长关系。可见，ROM LUT法很难兼顾功耗、性能、成本三方面，而CORDIC算法的应用能够很好地解决这一问题。

　　3.相位相加器将相位寄存器中的数字相位与相位控制字相加，得到偏移后的当前相位。

　　设系统的时钟频率为fc，频率控制字为M，相位寄存器位数为N，则数控振荡器输出信号频率为。根据Nyquist抽样定理，fs值为1/2fc，而在实际设计中，一般不应大于时钟频率的1/4。其频率分辨率为，根据此式，在系统时钟频率不变的情况下，相位寄存器位数N越大，产生信号的频率分辨率越高。

性能参数

　　NCO的性能指标包括信号频率分辨率、信噪比(SNR)、无杂散动态范围(SFDR)和输出的信号正交性。这些性能指标取决于NCO的数据位数。NCO的数据位数包括用于表示相位数据的位数n和表示相位的正弦值数据的位数nb，二者之间存在nb取决于n的关系，且前者必须能够表示相位变化时其相位正弦值变化的最小值和值。而这又分为两种情况：

　　种情况是相位最小变化值的正弦值最小变化发生在π/2-△φ～π/2，π/2～π/2+△φ，3π/2-△φ～3π/2，3π/2～3π/2+△φ，同时其相位的取值是在0～2π间且等间隔地分为2n爪取值点，因此，由正弦波的特性可知：只需要讨论相位在π/2-△φ与π/2取值点的正弦值之差，

　　第二种情况是相位最小变化值的正弦值的变化发生在0～△φ，π-△φ～π，π～π+△φ，2π-△φ～2π取值点处。该情况可以通过类似于种情况的推导方法得到。

　　NCO的噪声是因为存在正弦值的量化误差而引入的，且量化误差由表示正弦值的位数决定。

原理

　　下图为 NCO 的工作原理框图:

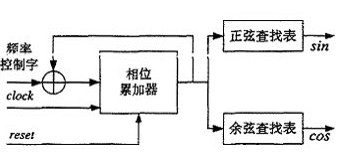
　　数控振荡器一般由基准时钟(fclk)、相位字寄存器、相位累加器以及幅度/相位转换电路等部分组成。在基准时钟的作用下，每一个时钟周期存贮在相位字寄存器里的值都由相位累加器进行累加，相位果加器的输出作为查找表的输人，从而得到相对应的幅度值。根据奈奎斯特采样定律，输出信号的频率应小于基准时钟的 1/2。

　　相位累加器输出(△Ф)的数值和系统的频率(fclk)决定了输出频率(fout),它门的关系如下:

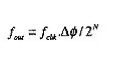
　　N是相位寄存器的位数，N 值的大小决定了频率分辨率(fres )，有

　　在这里假设，fclk=128MHz, N=32，可以计算出 NCO 的频率分辨率

　　fres=0.0298Hz

　　相位累加器是决定 NCO 电路性能的一个关键部分。我们可以采用了Altera的加法器宏功能模块形成一个32bit的累加器，它以流水线处理方式进行工作。

　　相位/幅 度转换电路是NCO 电路中的另一个关键部分，在设计中面临的主要问题就是资源的开销。

　　一般电路采用ROM 结构，相位累加器的输出是一种数字式锯齿波，通过取它的若干位作为 ROM的地址输人，而后通过查表和运算，ROM就能输出所需波形的量化数据。