自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的数字滤波器。根据环境的改变，使用自适应算法来改变滤波器的参数和结构。一般情况下，不改变自适应滤波器的结构。而自适应滤波器的系数是由自适应算法更新的时变系数。即其系数自动连续地适应于给定信号，以获得期望响应。自适应滤波器的最重要的特征就在于它能够在未知环境中有效工作，并能够跟踪输入信号的时变特征。
以输入和输出信号的统计特性的估计为依据，采取特定算法自动地调整滤波器系数，使其达到滤波特性的一种算法或装置。自适应滤波器可以是连续域的或是离散域的。离散域自适应滤波器由一组抽头延迟线、可变加权系数和自动调整系数的机构组成。附图表示一个离散域自适应滤波器用于模拟未知离散系统的信号流图。自适应滤波器对输入信号序列x(n)的每一个样值，按特定的算法，更新、调整加权系数，使输出信号序列y(n)与期望输出信号序列d(n)相比较的均方误差为最小，即输出信号序列y(n)逼近期望信号序列d(n)。
20世纪40年代初期，N.维纳首先应用最小均方准则设计线性滤波器，用来消除噪声、预测或平滑平稳随机信号。60年代初期，R.E.卡尔曼等发展并导出处理非平稳随机信号的时变线性滤波设计理论。维纳、卡尔曼－波色滤波器都是以预知信号和噪声的统计特征为基础，具有固定的滤波器系数。因此，仅当实际输入信号的统计特征与设计滤波器所依据的先验信息一致时，这类滤波器才是的。否则，这类滤波器不能提供性能。70年代中期，B.维德罗等人提出自适应滤波器及其算法，发展了滤波设计理论。
以最小均方误差为准则设计的自适应滤波器的系数可以由维纳-霍甫夫方程解得
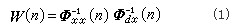
式中W(n)为离散域自适应滤波器的系数列矩阵Φxx-1(n)为输入信号序列x(n)的自相关矩阵的逆矩阵,Φdx(n)为期望输出信号序列与输入信号序列x(n)的互相关列矩阵。
B.维德罗提出的一种方法，能实时求解自适应滤波器系数，其结果接近维纳－霍甫夫方程近似解。这种算法称为最小均方算法或简称 LMS法。这一算法利用最陡下降法，由均方误差的梯度估计从现时刻滤波器系数向量迭代计算下一个时刻的系数向量
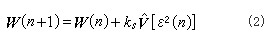
式中【ε2(n)】为均方误差梯度估计，
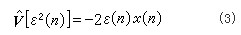
ks为一负数，它的取值决定算法的收敛性。要求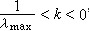
，其中λmax为输入信号序列x(n)的自相关矩阵特征值。
自适应 LMS算法的均方误差超过维纳滤波的最小均方误差，超过量称超均方误差。通常用超均方误差与最小均方误差的比值（即失调）评价自适应滤波性能。
抽头延迟线的非递归型自适应滤波器算法的收敛速度，取决于输入信号自相关矩阵特征值的离散程度。当特征值离散较大时，自适应过程收敛速度较慢。格型结构的自适应算法得到广泛的注意和实际应用。与非递归型结构自适应算法相比，它具有收敛速度较快等优点。人们还研究将自适应算法推广到递归型结构；但由于递归型结构自适应算法的非线性，自适应过程收敛性质的严格分析尚待探讨，实际应用尚受到一定限制。
●自适应反馈消除（en:Adaptive Feedback Cancellation）
●噪声消除（en:Noise cancellation）
●通道辨识（en:Channel identification）
●通道均衡
●信号预测
