加于其上的电压和电流之间的关系可用线性的代数或微分方程来描述的元件,称为线性元件。电阻、电容和电感元件是线性元件。由线性元件组成的电路,称为线性电路。
对线性网络的分析,可采用克希霍夫定理进行,也可有以下定理:
1 叠加定理
在线性网络中,若含有两个或两个以上的独立源,每一元件的电流或电压,可以看作是每一个独立源单独作用于网络时在该元件上产生的电流或电压之和,这就是叠加定理。
运用叠加定理时应该注意:考虑任一独立源单独作用时,其它独立源应视为零值,即独立电压源用短路代替,独立电流源用开路代替;而全部受控源则必须保留。
还须指出:在分析电路时,我们既要假定电流的参考方向,又要假定电压的参考极性。如果电流的计算结果为正值,表明电流的真实方向与参考方向一致。在未标示参考方向的情况下,电流的正、负结果是毫无意义的,对电压也如此。电流的参考方向和电压的参考极性,可以彼此无关的任意假设,但为方便起见,常采用“关联”参考方向,即假定电流的参考方向与电压的参考极性一致。
2 戴文宁定理
戴文宁定理的内容是:任一线性有源单口网络,可用一个电压源串联一个阻抗来代替,电压源的电压等于该网络端口的开路电压,而等效阻抗则等于该网络中全部独立源为零值时从端口看进去的阻抗。由这一电压源和等效阻抗组成的等效电路,称为戴文宁等效电路。
应用戴文宁定理时,还有两个问题必须注意:①由戴文宁定理所得的等效电路,只对网络的外部电路等效,即只适用于计算外部电路的电压和电流,而不适用于计算网络内部的电压和电流;②只要单口网络内部是线性的,外部电路即使是含有非线性元件的非线性电路,戴文宁定理同样适用。
3 诺顿定理
一个有源线性单口网络,可用一个电流源并联一个等效阻抗来代替,电流源等于该网络端口的短路电流,等效阻抗等于该网络中全部独立源为零值时从端口看进去的阻抗,这就是诺顿定理。电流源与等效阻抗并联的电路,称为诺顿等效电路。
4 密勒定理
线性电路的最基本的特性是它具有叠加性和均匀性。叠加性和均匀性的含义可以用下面的图来说明。
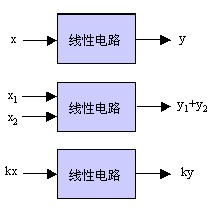
图中的方框表示电路,x 表示加在电路上的输入信号,或称激励;y 表示电路对该输入信号产生的输出,或称响应。叠加性的含义是:若激励x1产生的激励为y1, 激励x2产生的激励为y2,则当 x1 与 x2 共同作用于电路时产生的响应为 y1 + y2 。均匀性的含义是:若激励 x作用于电路产生的响应为 y,则激励 ky 做用于电路产生的响应必为 ky 。换句话说,线性电路对于各个激励共同作用的响应是各个激励的加权之和。
严格说来,真正的线性电路在实际中是不存在的。但是大量的实际电路在一定条件下都可以近似视为线性电路。在电路理论中,对线性电路的研究已经有了相当长的历史,有了成熟的理论和方法。
1 支路电流法 支路电流法支路电流法是以各支路电流为变量列写电路方程进而分析电路的一种方法。如果利用元件的VCR约束,将电路中的电压用电流代替,联立方程数目则减少了b个。电路以b个支路的电流为未知量得到b个KCL和 KVL方程。这种方法称为支路电流法,或1b法。
2 节点电压法对于包含b条支路n个节点的电路,若假设任一节点作为参考节点,则其余n-1个节点对于参考节点的电压称为节点电压。节点电压是一组独立完备的电压变量。以节点电压作为未知变量并按一定规则列写电路方程的方法称为节点电压法。一旦解得各节点电压,根据KVL可解出电路中所有的支路电压,再由电路各元件的VCR关系可进一步求得各支路电流。
3 割集分析法选取树支电压作为独立完备的电压变量分析电路的一种方法。对于包含树支电压的n-1 个基本割集列写n-1个KCL方程,将各支路电流用相关电导和树支电压表示。通过求解方程组解出割集电压,进而可以求出各支路电压和电流。割集分析法定义: www.docin.com 对于某一给定网络,若使用割集分析法分析电路,首先要选定该网络的一种树,确定树支连支,然后对其编号,并标注树支连支电压方向。然后确定基本割集,再对每个割集列写基本KCL方程。
4 网孔电流法定义:网孔电流法是以网孔电流作为电路变量列写方程求解的一种方法。注意:网孔电流是一种沿着网孔边界流动的假想电流。选取网孔电流作为电路变量,对网孔列写b-n+1个独立的KVL方程,将各支路电压以网孔电流与电阻的乘积表示,求b-n+1个网孔电流变量,其后再根据KCL,元件的VCR求出全部支路电流及电压。