压阻式压力传感器

原理

结构如图所示。
其核心部分是一块沿某晶向(如〈1 0〉)切割的N型的圆形硅膜片（见图2－35(b)）。在膜片上利用集成电路工艺方法扩散上四个阻值相等的P型电阻。用导线将其构成平衡电桥。膜片的四周用圆硅环（硅杯）固定，其下部是与被测系统相连的高压腔，上部一般可与大气相通。在被测压力P作用下，膜片产生应力和应变。膜片上各点的应力分布由式（2－20）和式（2－21）给出。当时，径向应力为零值。四个电阻沿〈1 1 0〉晶向并分别在x=0.635r处的内外排列，在0.635r之内侧的电阻承受的为正值，即拉应力（见图2－25(b)），外侧的电阻承受的是负值，即压应力。由于〈1 1 0〉晶向的横向为〈0 0 1〉，因此，，代入式（2－29）内外电阻的相对变化为式中 、——内、外电阻上所承受径向应力的平均值。设计时，要正确地选择电阻的径向位置，使,因而使。使四个电阻接入差动电桥，初始状态平衡，受力P后，差动电桥输出与P相对应。为了保证较好的测量线性度，要控制膜片边缘处径向应变。而膜片厚度为h≥式中 ——;膜片边缘允许的径向应变。　压阻式压力传感器由于弹性元件与变换元件一体化，尺寸小，其固有频率很高，可以测频率范围很宽的脉动压力。固有频率可按下式计算式中 ——硅片的密度（kg/m2）　压阻式压力传感器广泛用于流体压力、差压、液位等的测量。特别是它的体积小，最小的传感器可为0.8mm，在生物医学上可以测量血管内压、颅内压等参数。

应用

压阻式传感器广泛地应用航天、航空、航海、石油化工、动力机械、生物医学工程、气象、地质、地震测量等各个领域。在航天和航空工业中压力是一个关键参数,对静态和动态压力,局部压力和整个压力场的测量都要求很高的精度。压阻式传感器是用于这方面的较理想的传感器。例如,用于测量直升飞机机翼的气流压力分布，测试发动机进气口的动态畸变、叶栅的脉动压力和机翼的抖动等。在飞机喷气发动机中心压力的测量中，使用专门设计的硅压力传感器,其工作温度达500℃以上。在波音客机的大气数据测量系统中采用了精度高达0.05%的配套硅压力传感器。在尺寸缩小的风洞模型试验中，压阻式传感器能密集安装在风洞进口处和发动机进气管道模型中。单个传感器直径仅2.36毫米，固有频率高达300千赫,非线性和滞后均为全量程的±0.22%。在生物医学方面,压阻式传感器也是理想的检测工具。已制成扩散硅膜薄到10微米,外径仅0.5毫米的注射针型压阻式压力传感器和能测量心血管、颅内、尿道、子宫和眼球内压力的传感器。图3是一种用于测量脑压的传感器的结构图。压阻式传感器还有效地应用于爆炸压力和冲击波的测量、真空测量、监测和控制汽车发动机的性能以及诸如测量枪炮膛内压力、发射冲击波等兵器方面的测量。此外，在油井压力测量、随钻测向和测位地下密封电缆故障点的检测以及流量和液位测量等方面都广泛应用压阻式传感器。随着微电子技术和计算机的进一步发展，压阻式传感器的应用还将迅速发展。

压阻式传感器的应变与温度交叉灵敏度分析

应变与温度交叉灵敏度计算公式的给出
压阻式传感器是在圆形硅膜片上扩散出四个电阻，这四个电阻接成惠斯登电桥。假设四个扩散电阻的起始电阻都相等且为R，当有应力作用时，两个电阻的阻值增加，增加量为ΔR，两个电阻的阻值减小，减小量为ΔR；另外由于温度影响，使每个电阻都有ΔRT的变化量。若电桥的供桥电压为U，则它的输出电压为：
式中：πL—压阻系数；E—电阻半导体材料的弹性模量；S=πL·E—传感器的灵敏度。
根据四个电阻本身的温度特性，设它们的温度系数为α，则：
当传感器受应变ε和温度T的作用，则由泰勒公式在初始应变ε0和环境温度T0下将式(4)展开得：
灵敏度，当不考虑温度影响时，该项为常值；SεT=USα，定义为应变与温度的交叉灵敏度。
第三项、第四项及以后各项为温度变化项，忽略掉ΔT的高阶项，温度与传感器的输出呈线性关系，令ST=USεα，定义为传感器的温度灵敏度。忽略掉高阶项，式(6)又可写为：
很显然，考虑交叉灵敏度的非线性方程(7)与线性近似的方程(8)相比，求得的应变和温度与实际值较为接近；但当被测量变化较小时，由式(8)可获得足够精确的解，且用线性方程近似求解可充分利用较为成熟的线性方程组的数值方法理沦，使问题大大简化，因此式(8)在实际应用中仍具有重要意义，而参量变化较大时，忽略交叉灵敏度对于求解精度影响较大。
交叉灵敏度分析
由交叉灵敏度公式SεT=USα可知：
交叉灵敏度既与传感器应变片自身的压阻系数、弹性模量、温度系数有关，又与电桥的供电电压有关，因此应变和温度同时作用于传感器时，传感器的输出不是应变和温度单独作用时产生的输出量的简单迭加，还存在着热力学和力学量的相互作用，这个作用反映为交叉灵敏度，其大小反映了这种相互作用的程度。
实际上，交叉灵敏度反映了在不同应变时，温度灵敏度不是一个常数，而是随着应变的变化而变化，交叉灵敏度的大小描述了温度灵敏度偏离常数的程度。实验中通过在不同应变下测量温度灵敏度，作出ST-ε曲线，该曲线的斜率便反映了交叉灵敏度的大小。
计算实例
以IC Sensors公司的S17-30A型传感器为例，结合A/D转换器AD7731把模拟量转换成数字量—6位16进制原码，再把16进制的原码送入AT89c52单片机，由单片机送出原码值。实验中以标准压力作为输入，测取不同温度条件下16进制的原码值，实验数据如表1所示。

由表1中的数据，利用方程(7)进行计算。首先在同一温度不同压力条件下，然后再在同一压力不同温度条件下借助MATLAB语言分别解矩阵得：

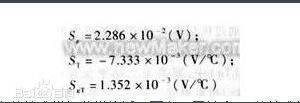
Sε，ST计算结果与传感器自身的技术指标非常接近，而交叉灵敏度SεT的技术指标只能通过上述方法或类似方法求出。
结论
利用上述方法借助方程(8)求出Sε，ST，通过对比可知，忽略交叉灵敏度将会带来很大的误差，该方法同样适用于其他半导体传感器。