在
电子电路的分析领域,虚断和虚短是分析
运算放大器电路的概念。通过这两个概念,能够极大地简化复杂电路的分析过程。下面我们将详细介绍虚断和虚短的概念,并利用它们对 11 个基本运放电路进行深入分析。
- 虚短:由于运放的电压放大倍数极大,一般通用型运算放大器的开环电压放大倍数都在 80dB 以上,而运放的输出电压是有限的,通常在 10V - 14V 之间。这就导致运放的差模输入电压不足 1mV,两输入端近似等电位,如同 “短路” 一般。“虚短” 指的是在分析运算放大器处于线性状态时,可把两输入端视为等电位,但显然不能将两输入端真正短路。
- 虚断:运放的差模输入电阻很大,一般通用型运算放大器的输入电阻都在 1MΩ 以上。因此流入运放输入端的电流往往不足 1uA,远小于输入端外电路的电流。所以通常可把运放的两输入端视为开路,且输入电阻越大,两输入端越接近开路。“虚断” 是指在分析运放处于线性状态时,可以把两输入端视为等效开路,同样不能将两输入端真正断路。
在分析运放电路工作原理时,我们先抛开同向放大、反向放大、加法器、减法器等输入输出关系的公式,也暂时不考虑输入偏置电流、共模抑制比、失调电压等电路参数,将实际放大器当作理想放大器来分析,这样能让我们更清晰地理解电路原理。
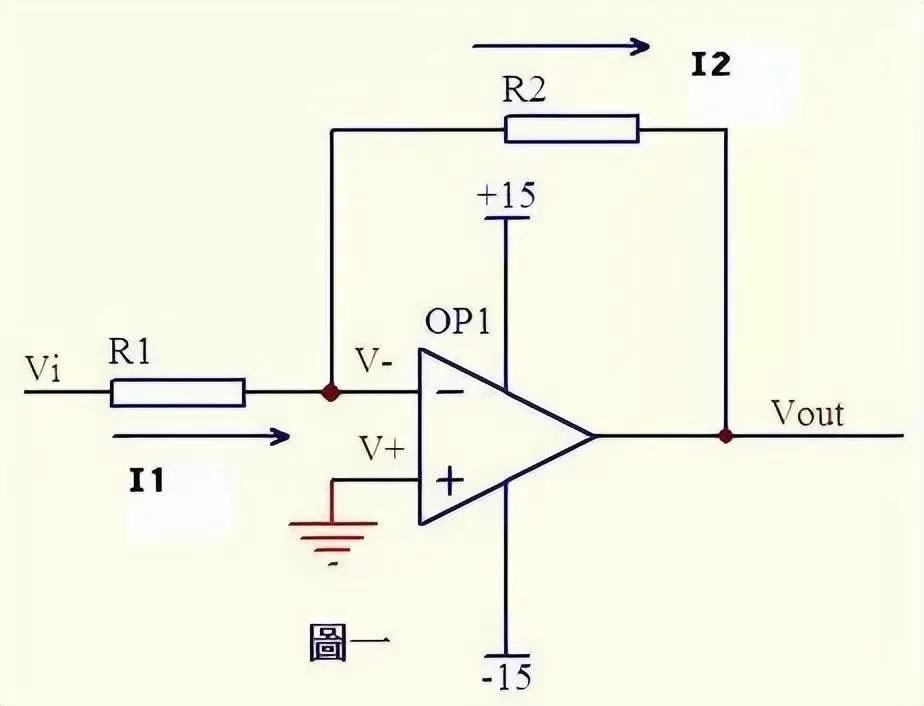
- 反向放大器:运放同向端接地为 0V,根据虚短,反向端也为 0V。又因为虚断,反向输入端几乎没有电流注入和流出,R1 和 R2 相当于串联,流过它们的电流相同。通过一系列计算可得反向放大器的输入输出关系式为Vout=(?R2/R1)?Vi。
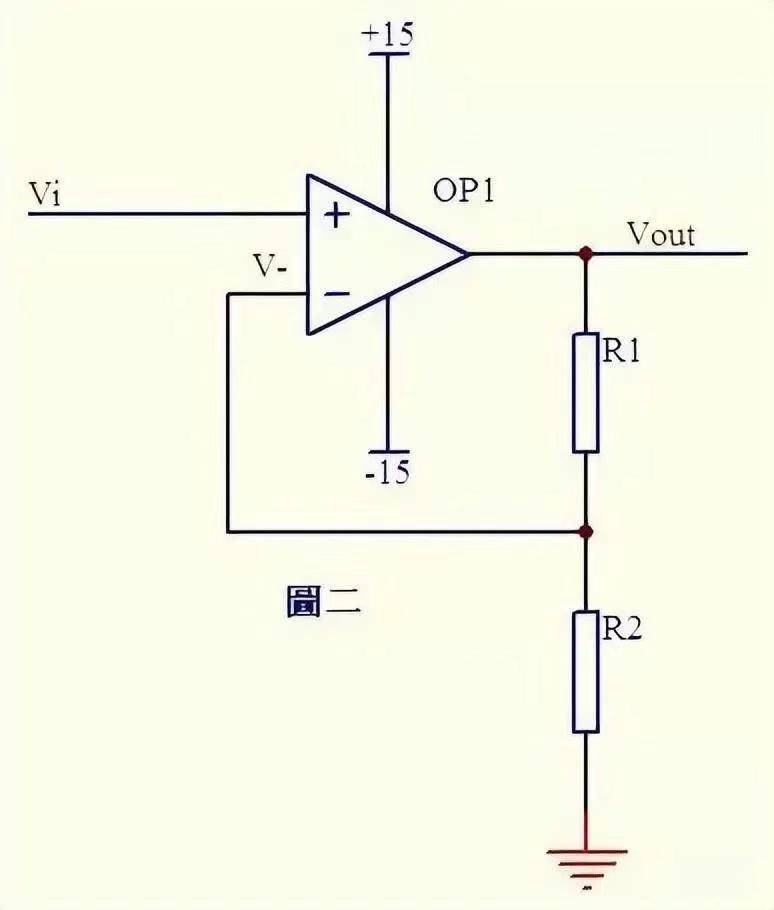
- 同向放大器:Vi与反向输入端虚短,即Vi=V?。由于虚断,反向输入端无电流输入输出,通过 R1 和 R2 的电流相等。经推导可得同向放大器的公式为Vout=Vi?(R1+R2)/R2。
- 加法器 1:由虚短可知反向端和同向端电压为 0V,根据虚断及基尔霍夫定律,通过 R2 与 R1 的电流之和等于通过 R3 的电流。若取R1=R2=R3,则可得?Vout=V1+V2,这就是加法器的原理。
- 加法器 2:因为虚断,运放同向端无电流流过,所以流过 R1 和 R2 的电流相等,流过 R4 和 R3 的电流也相等。若R1=R2,R3=R4,可推导出Vout=V1+V2,同样实现了加法功能。
- 减法器:由虚断可知通过 R1 和 R2 的电流相等,通过 R4 和 R3 的电流相等。若R1=R2,R3=R4,再结合虚短,可得出Vout=V2?V1,即实现了减法运算。
- 积分电路:根据虚短,反向输入端电压与同向端相等;由虚断可知,通过 R1 的电流与通过 C1 的电流相等。经推导可得输出电压与输入电压对时间的积分成正比,即Vout=((?1/(R1?C1))∫V1dt。若V1为恒定电压 U,则Vout=?U?t/(R1?C1),输出电压是一条从 0 至负电源电压按时间变化的直线。
- 微分电路:由虚断可知通过电容 C1 和电阻 R2 的电流相等,由虚短可知运放同向端与反向端电压相等。则Vout=?i?R2=?(R2?C1)dV1/dt,这是一个微分电路。若V1是突然加入的直流电压,输出Vout对应一个方向与V1相反的脉冲。
- 差分放大电路:根据虚短和虚断,可得出Vout=(Vy?Vx)(R1+R2+R3)/R2,其中(R1+R2+R3)/R2是定值,确定了差值(Vy?Vx)的放大倍数,这就是差分放大电路。
- 电流检测:很多控制器接收 0 - 20mA 或 4 - 20mA 电流,需将其转换成电压后送 ADC 处理。通过虚短和虚断分析,可将 4 - 20mA 电流转换成 - 0.88 - -4.4V 电压,若将电流反接则得到 + 0.88 - +4.4V 电压。
- 电压电流转换检测:该电路中负反馈通过三极管 Q1 的发射结串联,只要是放大电路,虚短虚断规律依然适用。经分析可得R7两端的电压和输入电压Vi相等,通过R7的电流I=Vi/R7,若负载RL<<100KΩ,则通过RL和R7的电流基本相同。
- 传感器检测:以三线制 PT100 前置放大电路为例,通过虚短和虚断分析,可得出输出电压V5是Rx的函数。若测出V5、V6的值,就可算出Rx及R0,进而通过查 pt100 分度表知道温度的大小。