在
电子电路领域,DC/DC 变换电路是实现电压转换的重要组成部分,特别是非隔离的 6 大 DC/DC 电路,在众多电子设备中有着广泛的应用。下面我们就来详细了解一下这 6 种电路。
Buck 电路主要是基于斩波原理来控制直流源的输出电压。如图 1 所示,一个负载 R 通过
开关 S 连接
电源。当开关 S 周期性地断开和闭合时,负载 R 也会周期性地接通和断开。若负载 R 是灯泡,在开关频率较低时,灯泡会闪烁;当频率逐步升高,人眼就无法看清其闪烁,而是以灯泡的亮度来体现。对于一定输入电压的斩波电路,其输出电压平均值是通过周期性断开和闭合电路中的开关进行控制的。图中 D 为电路的占空比,即开关 S 闭合的时间与闭合和开断时间总和的比值,通过调节 D 可以调节电路的输出电压。
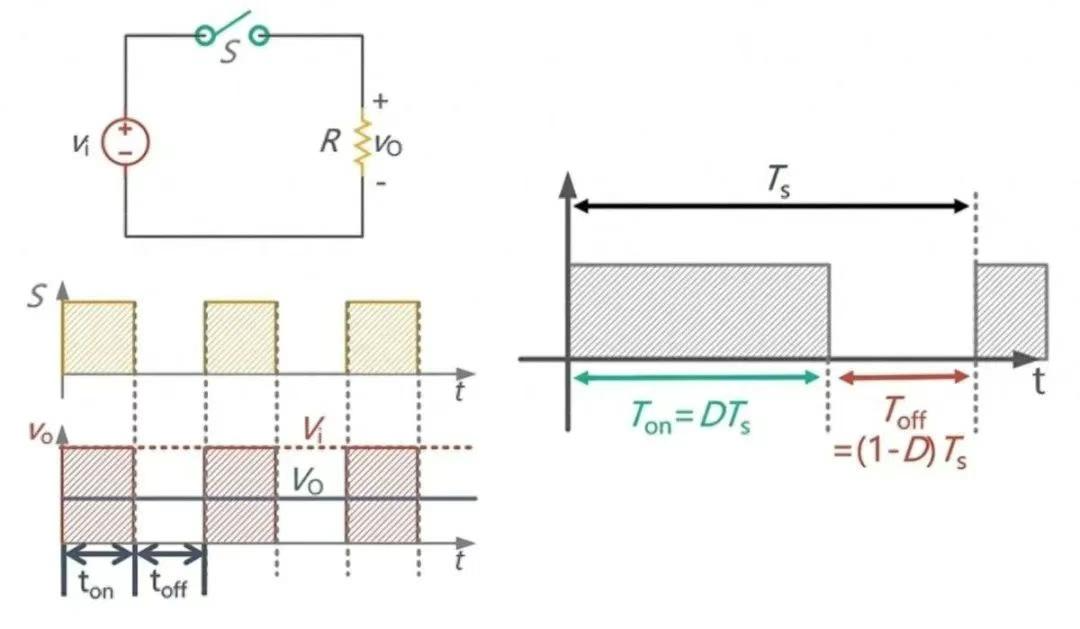
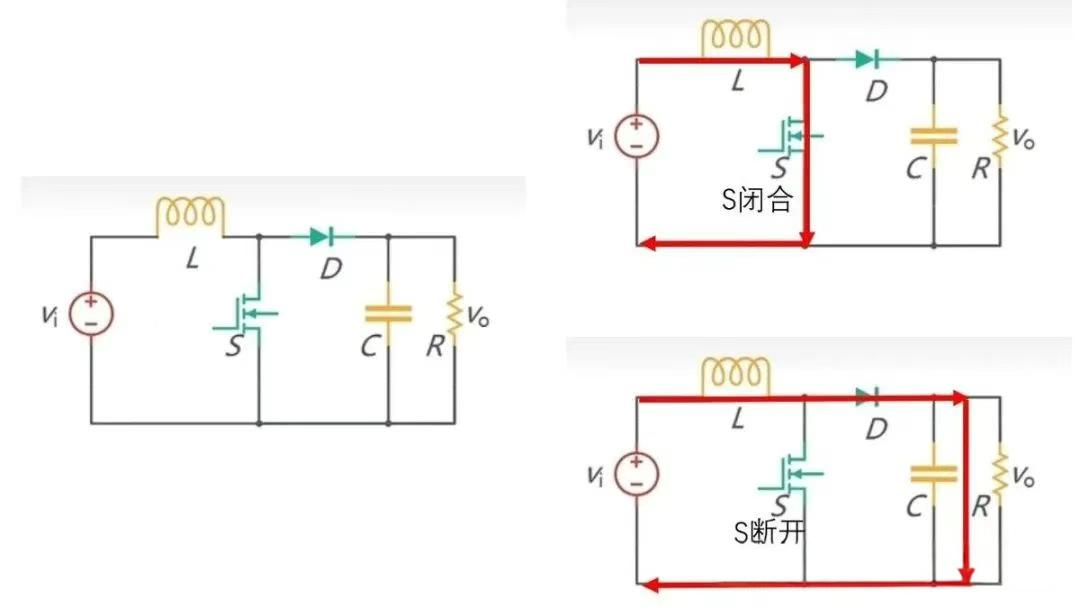
图 2 显示了 Buck 电路的工作过程,整个工作分成两个部分。当 S 闭合时,
电感存储能量并且电源给负载供电;当 S 断开后,由于电感电流不能突变,电感电流通过续流
二极管继续给负载供电。因此负载 R 的输出电压为 Vo = DVi。

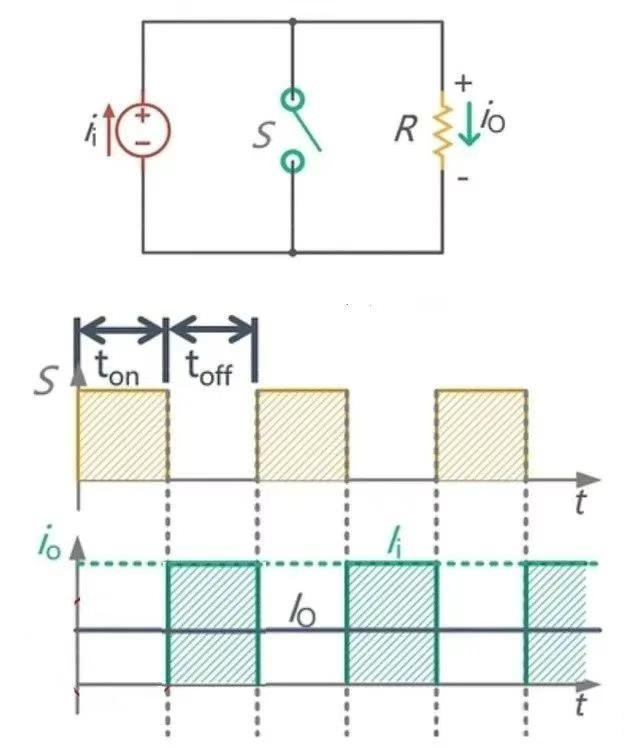
Buck 电路是通过对电压源进行周期性的开断 S 来实现输出电压的降压。在不考虑电路自身损耗的情况下,输入功率等于输出功率。在直流系统中,功率等于电流乘以电压,若想得到高电压,就需要降低电流以保证功率不变。因此,可以通过斩波来实现电流的降低,从而实现 Boost 电路。电流的斩波电路和 Buck 电路是对偶关系,如图 3 所示。当开关 S 断开时,负载 R 处流过电流;当开关 S 闭合后,负载 R 被开关短路,电流为 0。所以 Io = (1 - D) Ii,其对应的输出电压为 Vo = 1/(1 - D) Vi。
将上述电路进行变化,选择一个大的电感和电压源串联来表示电流源,开关 S 用半导体器件代替,再加上一个续流二极管就变成了 Boost 电路,如图 4 所示。当 S 闭合,电压源给电感充电,电感存储能量;当 S 断开,电压源和电感同时给负载供电,达到提升电压的目的。
如果将 Buck 电路输入接直流源,输出作为 Boost 电路的输入,即构成前端 Buck 后端 Boost 的两级变换器,就可以实现升降压功能,如图 5 所示。
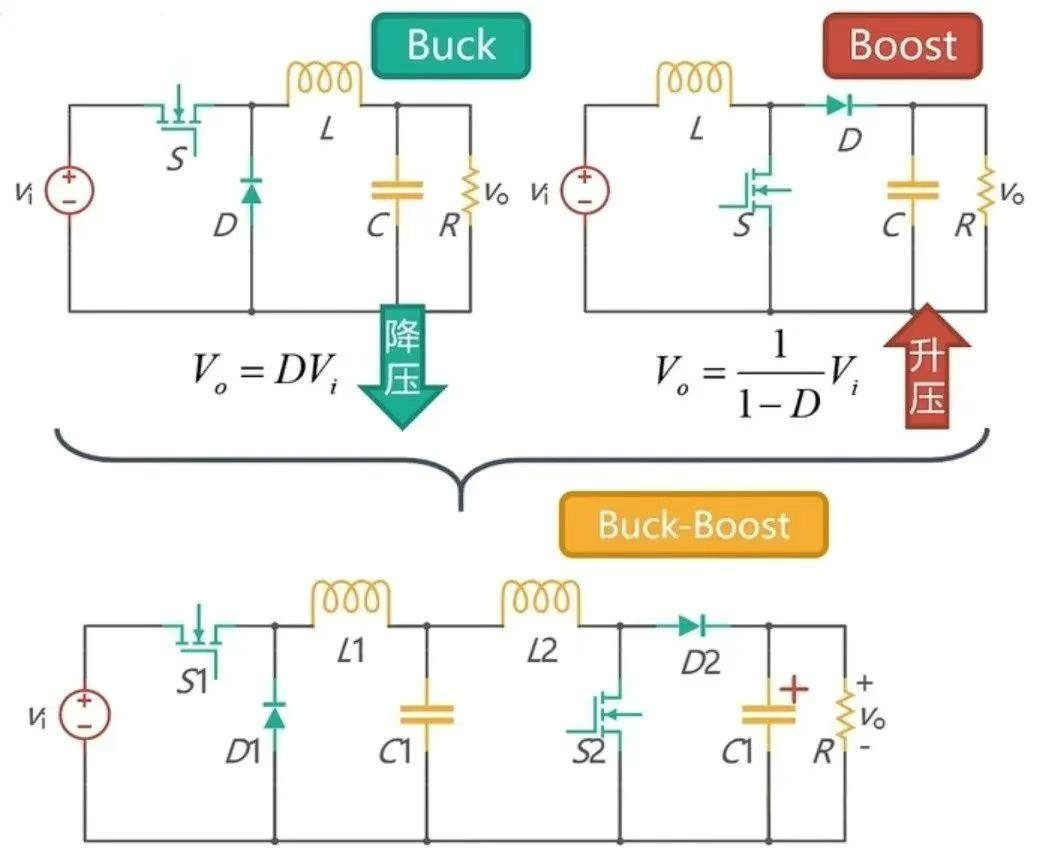
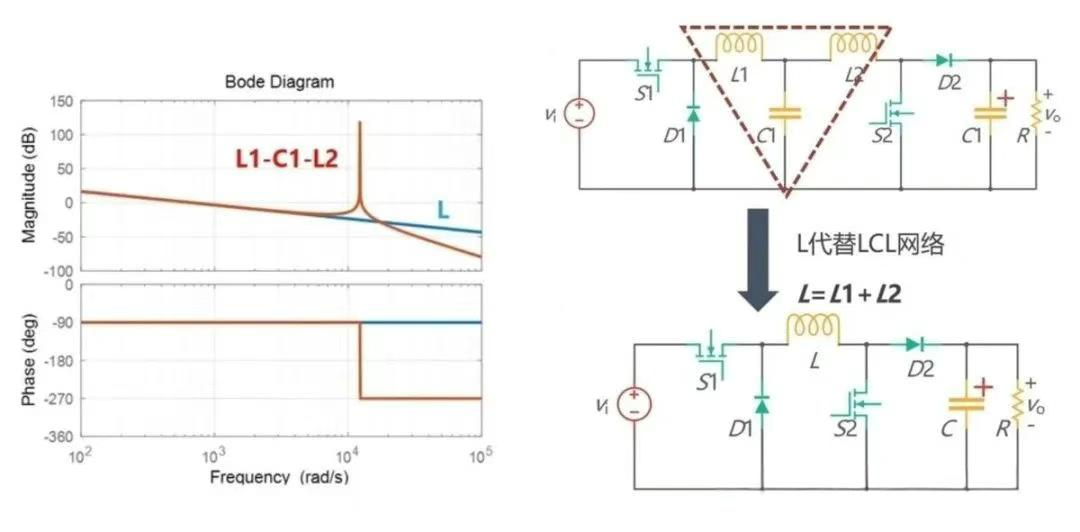
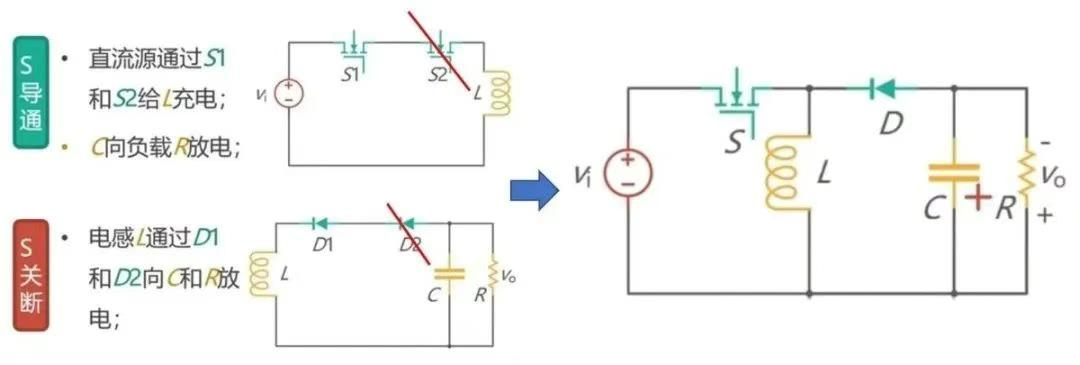
通过把 Buck 电路和 Boost 电路公式进行合并,可得出 V0 = D2/(1 - D1) Vi。接下来对 Buck - Boost 电路进行简化。首先对比 LCL 网络的动态特性和 L 网络的动态特性,通过波特图(图 6)可以看出,在低频阶段,两者的动态特性是一致的,因此可以用 L 来代替 LCL 网络。分别画出 S1 和 S2 同时导通和断开的图(图 7),可以发现 S1 和 S2 同时导通时是串联在一起进行充电,所以可以减去一个开关;S 同时关断时,两个二极管也是串联关系,也可以减去一个二极管。将两者合并后,就得到了 Buck - Boost 电路。
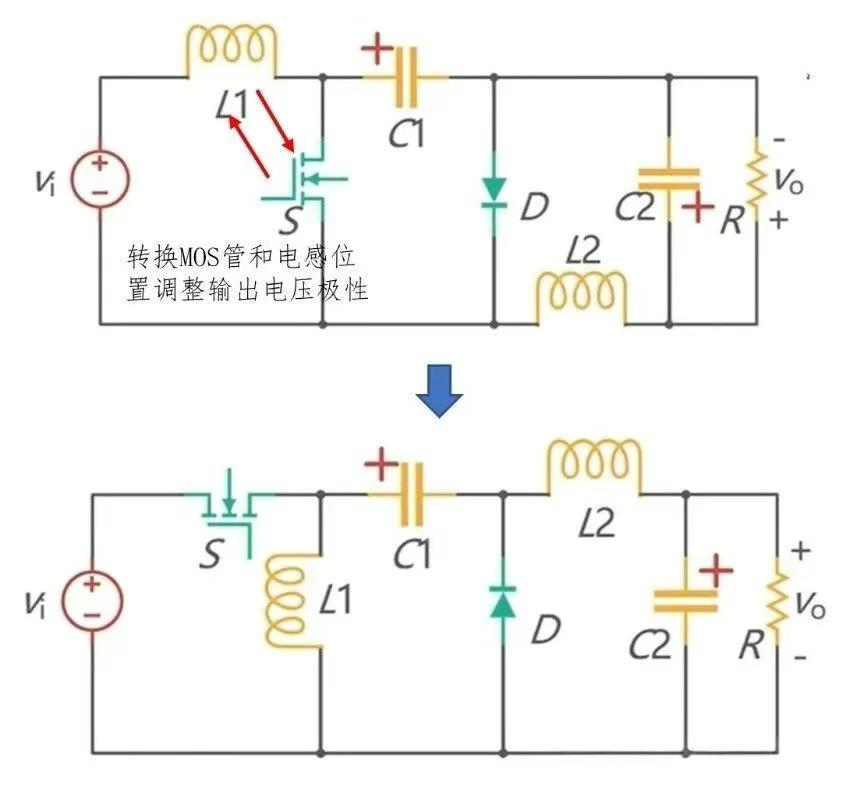
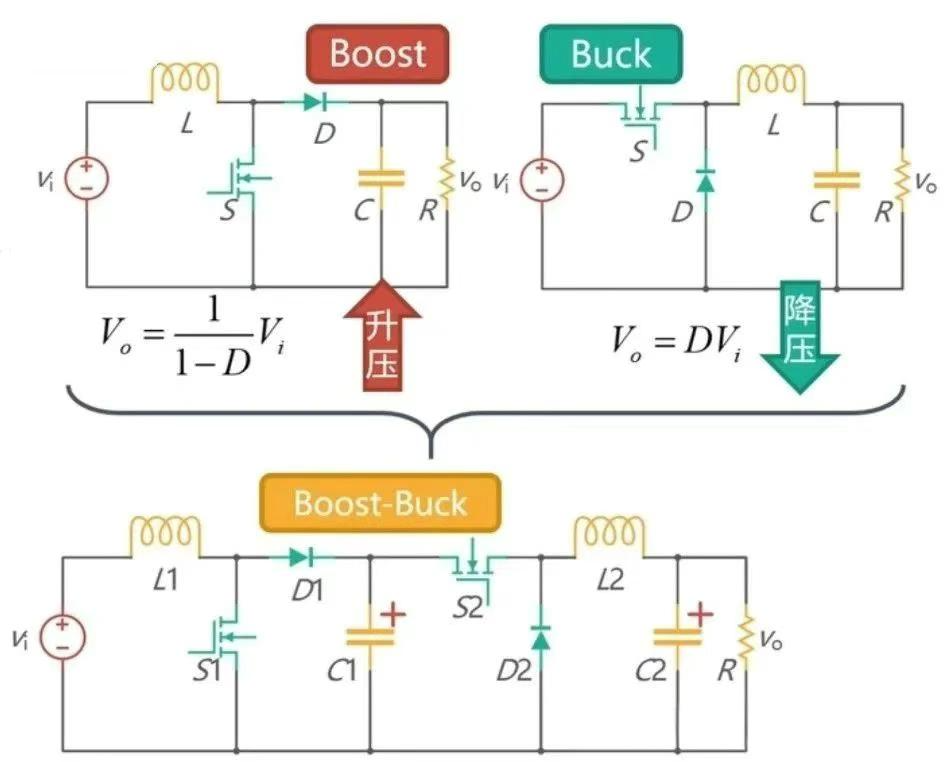
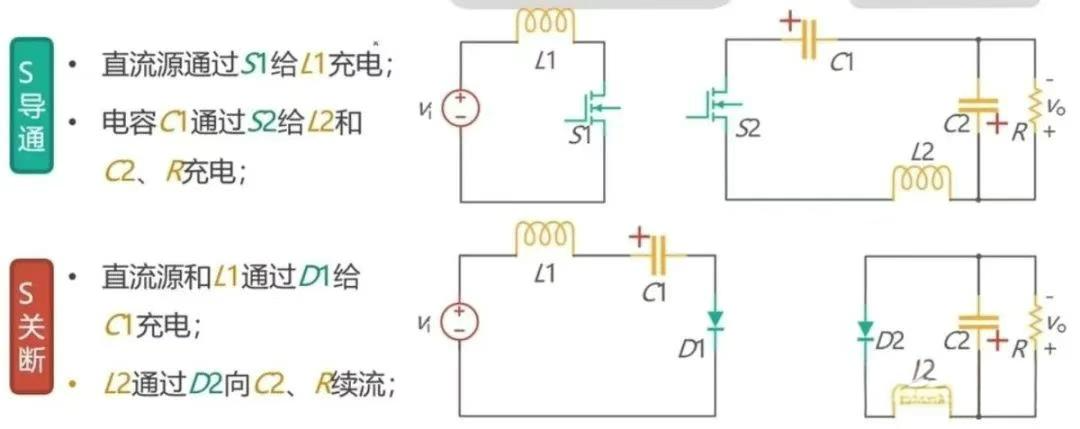
若将 Boost 电路输入接直流源,输出作为 Buck 电路的输入,Buck 电路的输出接负载,即构成前级 Boost 后级 Buck 的两级变换,如图 8 所示。简化方法和 Buck - Boost 电路类似,先确定 S1,S2 同时导通时的电路,再确定 S1 和 S2 同时断开时的电路,如图 9 所示。以电容 C1 为分界点,把 S1 和 S2 进行合并,同时把 D1 和 D2 进行合并终得到 Cuk 电路,如图 10 所示。Cuk 电路需要两个电容和电感,并且它的输出电压的极性和输入电压的极性相反。为了调整输出电压的极性,就演化出了 Speic 和 Zeta 电路。
Speic 电路(图 11)是对 Cuk 电路的改进,通过调整输出的回路,使得输入和输出的电压极性相同。Zeta 电路(图 12)则是调整输入端的结构,同样实现了输出电压的极性和输入电压的极性相同。
本篇文章详细介绍了非隔离的 DC/DC 电路的总共六种电路,其转换关系如图 13 所示。首先通过斩波得到了 Buck 电路,其次通过斩流得到了 Boost 电路。通过把先 Buck 再 Boost 的思路把 Buck 电路和 Boost 电路进行连接得到了 Buck - Boost 电路。与之对应,把 Boost 电路放在 Buck 电路之前,得到了 Boost - Buck(Cuk)电路。对于电路的化简,可以画出两个 MOS 管同时导通和关闭得到的等效电路进行化简。为了得到同样极性的输出电压,Cuk 电路又演化为 Speic 和 Zeta 电路。这些电路在不同的电子设备中发挥着重要作用,了解它们的原理和特性,对于电子电路的设计和应用具有重要意义。