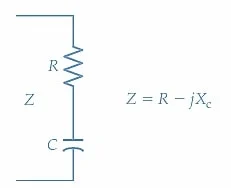在系列RC电路中，电阻器和电容器以串联配置连接，这意味着流过电路的电流依次通过两个组件。电阻抵抗电流的流动，而电容器以电场的形式存储能量。
　　图1（a）显示了由电容（C）和电阻（R）组成的串联电路， 并且分别在图1（b）和（c）中说明了电路的波形和相图。电流（i）的波形首先绘制，因为它与图1（b）中的两个连接组件（R和C）都是共同的。

　　跨电阻的电压（V r）与电阻通过电阻始终处于相相。因此，图1（b）中的V r的波形 与电流波形相相绘制。通过电容器的电流 导致电容器端子电压（V C）乘以90°；因此，v C 波形被绘制为90°落在电流波中。施加的电压E是两个组分电压V r 和V C的产生，它的波形可以通过简单地求和V R 和V C的瞬时水平来获得，并且可以看到E lags I lags I lags i lags i lags i lags i lags i lags i lags i lags i lags i lags i lags i lags i lags i。

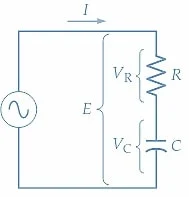
　　（a）系列RC电路

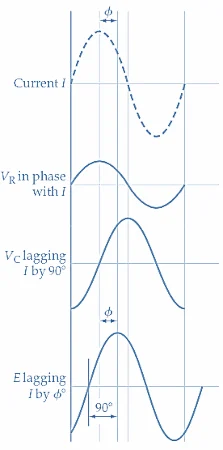
　　（b）电路波形

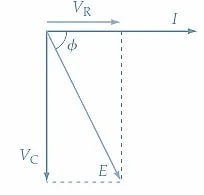
　　（c）相图
　　图1。 在串联的RC电路中，电流导致电容器电压（V C）乘以90°，并导致电源电压（E）的角度小于90°。图像由Amna Ahmad提供相图
　　串联RC电路的相图图 是通过再次从电流相量开始绘制的，因为电流是串联电路中的常见数量。将水平线绘制为表示电流（i）[图1（c）]的比例。由于电阻电压与i相同，因此V r 由与I的另一个水平线表示。电容器电压滞后i的i为90°，因此V c 相sor以-90°的角度绘制为-90°的角度。对于vAsor添加V C和V r的结果，v c 和v r 代表了applied voltage（e）。再，看到e的落在角度?上，该角度小于在纯电容电路中E和I之间存在的90°角。
　　电路方程
　　从图1（c）中，串联RC电路中E的矩形形式表达式为\ [e = v_ {r} -jv_ {c} \，（1）\] \]
　　或极地形式
　　\ [e = \ sqrt {v^{2} _ {r}+v^{2} _ {c}} \ Angle Tan-1 {\ big（} \ big（} \ frac {v_ {c}}}}
　　将等式1划分为i
　　\ [\ frac {e} {i} = \ frac {v_ {r}} {i} -j \ frac {v_ {v_ {c}}} {i} {i} \]
　　数量v r /i是电阻上电阻的电压除以电阻的电流。因此，V r /i可以用R替换。另外，v c /i是电容器通过电容器划分的电容器电压，可以用电容式电抗x c替换。数量E/I既不是电阻也不是电容电抗，因为它既有组成部分。在这种情况下，E/I被称为阻抗，并给出符号Z。因此，如图2所示，可以重述上述方程式。
　　\ [z = r-jx_ {c} \，（3）\]
　　在公式3中，r在欧姆中具有抗性，x c 是欧姆的电容电抗，而z在欧姆中是阻抗。还，\ [| z | = \ sqrt {r^{2}+x^{2} _ {c}}} \，（4）\] \]
　　和

　　\ [\ phi = tan-1 {\ big（} \ frac {-x_ {c}}} {r} {r} {\ big）} \，（5）\] \]

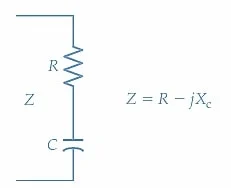
　　图2。 由电阻和电容器组成的电路的阻抗为（z = r -x c）。图像由Amna Ahmad提供组合公式4和5
　　\ [z = \ sqrt {r^{2}+x^{2} _ {c}}} \ angle-tan-tan-1 {\ big（} - \ frac {x_ {x_ {c}}}} {r} {r} {\ big）{\ big）}}
　　方程式6表示从矩形形式（z = r +jx）到极性形式（ZBent）的转换。
　　阻抗图

　　正如串联RL电路所解释的那样，数量z，r和x c 不是量度数量，因为它们具有固定值。为了区分阻抗，电抗和抗性的矢量图与相图图，通常以三角形形式绘制，被称为阻抗图。串联RC电路的阻抗图如图3所示。首先将水平线绘制为刻度表示R，然后与R相对于R的-j分量（x c）在-90°下绘制。

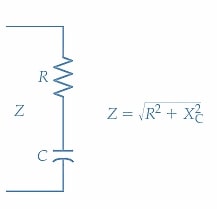
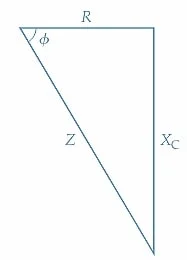
　　图3。 用于串联的RC电路的阻抗图（或阻抗三角形）。电容电抗向量X C 以-90°角从电阻矢量中绘制（向下）。阻抗矢量z是R和X c的结果。图像由Amna Ahmad提供准入
　　与电导率（电阻的倒数）和感应（反应的倒数）一样，阻抗的倒数是一个重要数量，可以在电路分析中有效地应用。接纳（符号y）是阻抗（z）的倒数，其单位是西门子。
　　准入：
　　\ [y = \ frac {1} {z} \，（7）\] \
　　当z在公式7中的欧姆中表达时，y在西门子中。
　　串联RC电路的分析程序
　　分析系列RC电路时，请按照以下步骤操作。
　　1。计算电容电抗\（x_ {c} = \ frac {1} {2 \ pi fc} \）2。如果有多个电阻组件，请计算总电阻
　　\ [r = r_ {1}+r_ {2}+... \]
　　3。计算阻抗
　　\ [| z | = \ sqrt {r^{2}+x^{2} _ {c}}} \] \]
　　4。计算相位角\（\ phi = tan-1 {\ big（} \ frac {x_ {c}}} {r} {r} {\ big）} \）5。计算当前\（i = \ frac {e} {z} \）
　　6。确定电阻电压\（v_ {r} = ir \，或\，v_ {r} = e \，cos \，cos \ phi \）7。确定电容电压\（v_ {c} = ix_ {c} \或\，v_ {c} = e \，sin \，sin \，sin \，\ phi \）示例1

　　分析图4中的串联RC电路，以确定电流的电流，电压，C跨C的电压以及相对于电源电压的电流的相角。

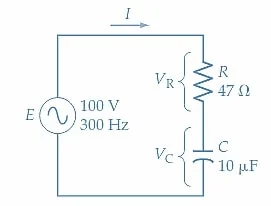
　　图4。 系列连接的RC电路示例。图像使用的图像由Amna Ahmad提供解决方案
　　电容电抗：
　　\ [x_ {c} = \ frac {1} {2 \ pi fc} = \ frac {1} {2 \ pi \ pi \ times300Hz \ times10 \ times10 \ mu f} \ act电路阻抗：
　　等式4
　　\ [| z | = \ sqrt {r^{2}+x^{2} _ {c}} = \ sqrt {（47 \ omega）^{2}+（53.1 \ omega）相角：
　　等式5
　　\ [\ phi = tan-1 {\ big（} \ frac {-x_ {c}} {r} {r} {\ big）} = tan-1 {\ big（} \ big（} \ frac {-53.1 \ omega}
　　电路电流：
　　\ [i = \ frac {e} {z} = \ frac {100v} {70.9 \ omega \ omega \ angle-48.5 \ geger} \ action} \ action}
　　参考系列RC电路相图图图1（c）：
　　电阻电压：
　　\ [v_ {r} = e \，cos \，cos \，\ phi = 100v \，cos \，cos {\ big（} -48.5 \ degr {\ big）} \ lig）电容器电压：
　　\ [v_ {c} = e \，sin \，sin \，\ phi = 100v \，sin \，sin {sin {\ big（} -48.5 \ grgu {\ big）} \ lig-74.7v {\ big big（}
　　示例2
　　绘制示例1中分析的串联RC电路的相图图。
　　解决方案
　　电流（i）的相类（i）首先是水平绘制的（见图5）。
　　V r 与电流相相。
　　V C 绘制落后90°的电流。

　　e将电流滞后于，也是V C 和V r的结果。

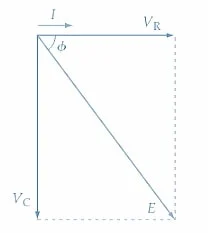
　　图5。 示例2中的串联RC电路的相图图。图像使用的图像由Amna Ahmad提供