什么是开关电容器电路？
　　开关电容器电路是一个离散的时间电路，可利用由开关控制的电容器输入和从电容器中的电荷传输。开关活动通常由定义明确的非重叠时钟控制，因此电荷转移进出是明确的和确定性的。

　　可以将这些电路视为样品和保持电路的类型，在该电路中，在该电路中采样并通过电路传递以实现所需功能。

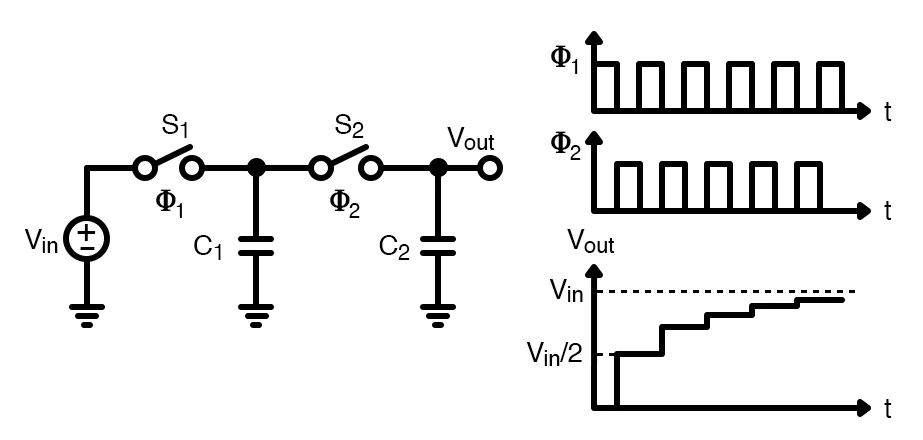
　　带有非重叠时钟的切换电容器电路
　　带有非重叠时钟的切换电容器电路。重新创建的图像使用了 Ma等人。
　　开关电容器电路在诸如滤波器设计之类的应用中非常流行，这要归功于其非常准确的频率响应以及良好的线性和动态范围。
　　正如我们稍后看到的那样，切换盘过滤器的离散时频响应完全由电容比和电路时钟频率设置，从而可以地将响应设置为0.1％的顺序。另一方面，连续时间过滤器基于RC时间常数设置其频率响应，由于过程变化，值可能会变化多达20％。
　　开关电容器电阻

　　开关电容器电路设计的基本构建块是开关电容器电阻。如前所述，该电路具有两个相同频率的非重叠时钟，即1和2。要分析该电路，我们将查看两个阶段。

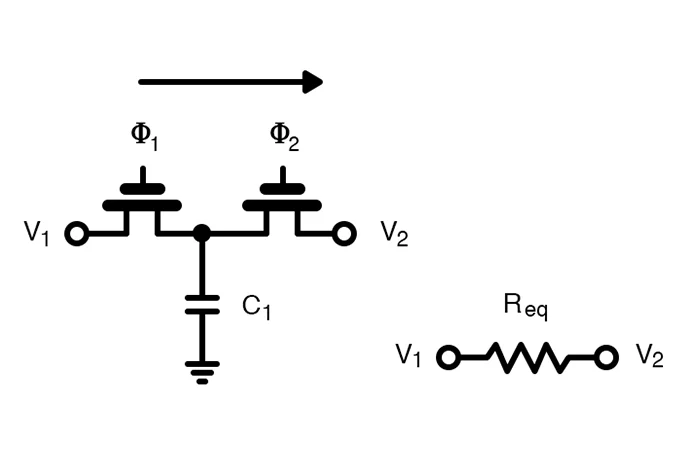
　　开关电容器电阻。
　　开关电容器电阻。重新创建的图像由Carusone等人提供。
　　在阶段，开关2关闭时打开开关1。在此设置中，电荷从节点V1流入电容器。在第二阶段，开关2关闭时，开关1打开。此时，C1连接到节点V2，并将充电或放电，直到电容器上的终电压为V2为止。该电荷在每个阶段的总价值都给出\ [q_1 = C_1V_1 \]
　　\ [q_2 = C_1V_2 \]
　　如果我们考虑总负荷变更，我们将获得以下方程式：
　　\ [\ delta q = c_1（v_1-v_2）= C_1 \ delta v \]
　　知道电流被定义为随时间的收费变化，并且我们的时间变化不过是我们的时钟周期，我们可以在此交换电容器上获得电流的平均值：
　　\ [i_ {eq} = \ frac {c_1（v_1 -v_2）} {t} = c_1 \ delta vf \]
　　，我们可以使用上述方程来找到电路的等效电阻：
　　\ [\ Mathbf {r_ {eq} = \ frac {t} {c_1} = \ frac {1} {c_1f}} \]
　　快速注意：我会被遗忘，更不用说先前的分析假设每个时钟周期传输的电荷在许多周期上是恒定的，从而使我们能够近似平均电流和电阻。对于输入信号相对于采样频率迅速变化的情况，需要进行离散的Z域分析。
　　区域节省和受控频率响应
　　从这些结果中，我们可以看到开关盖电路电路的魔力：它们允许设计人员创建非常紧密控制的电阻，仅取决于时钟频率和电容器值。

　　该技术的一个好处是它有助于节省空间。达到较大的电阻通常需要大量的硅面积。通过开关盖电路，这两个因素都可以显着较小。

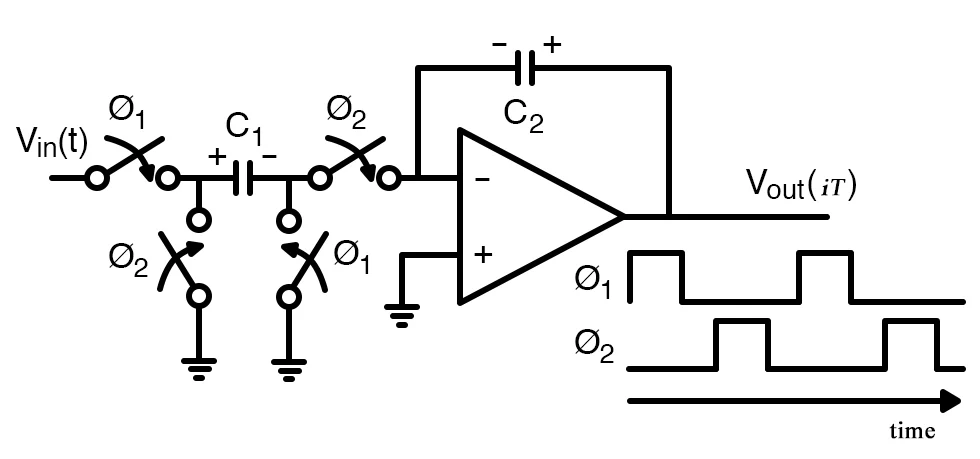
　　带有非重叠时钟的切换式电容器积分器
　　带有非重叠时钟的切换容量集成器。重新创建的图像由Tenhunen等人提供。
　　另一个好处是，在连续的RC滤波器中，电阻器和电容器之间的不匹配是限制的。与不同的设备（电容器的电容器）（电容器到电阻器），相似设备之间的匹配往往要好得多（电容器的电容器），从而使切换式置换过滤器具有频率响应更加。
　　，由于我们的电阻值是完全由电容值和频率设置的，因此我们可以通过更改时钟频率来动态更改过滤器的频率响应。
　　切换电容器电路的应用范围很广，这是有充分理由的。从过滤器到ADC的许多电路都利用这些技术的区域节省和严格控制的频率响应。