变阻器是简单且无处不在的电路元件，通常由一个电位计组成，该电位计连接为可调节的双端电阻器。电阻范围从欧姆到兆欧姆的手动电位器的可用性使标称电阻的选择变得容易。但是，当应用程序需要数字电位计 （Dpot） 时，问题可能很棘手。
　　与手动电位器相比，Dpots 仅在较窄的阻力范围内可用。它们通常还存在高 Wiper 电阻和电阻容忍度问题。这些限制共同使 Dpot 成为实现变阻器的困难介质。近的 EDN 设计理念 （DI） 文章通过各种策略和拓扑解决了这些问题：
　　虽然这些设计中的每一种都纠正了冗长的数字变阻器缺点列表中的一个或多个抱怨，但没有一个可以解决所有问题，有些还引入了自己的复杂性。示例包括交叉失真、对电阻容差的不降低灵敏度、编程电阻的分辨率降低非线性以及普通的旧复杂性。
　　设计
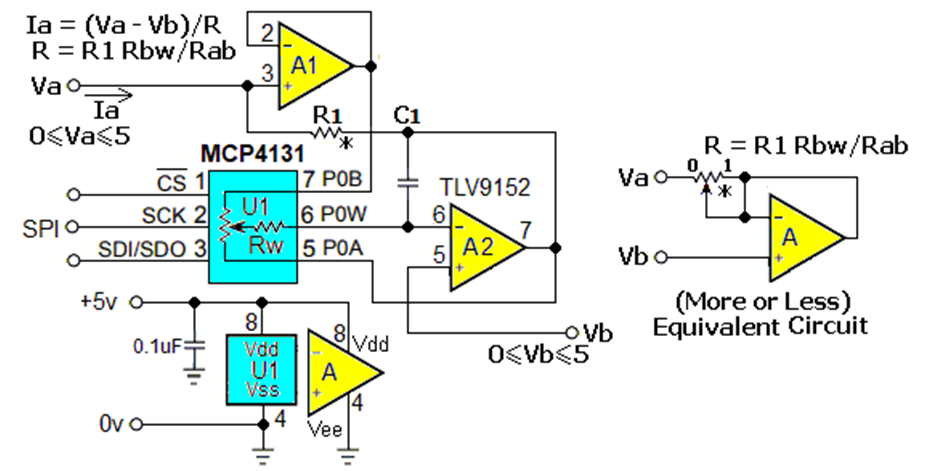
　　Figure 1 的电路也不是一个完美的解决方案。但它确实合成了一个的编程电阻，该电阻等于参考电阻 R1 线性乘以 U1 的 Rbw/Rab 数字设置（端子 B 与游标电阻与总元件电阻之间的比率）。
　　图 1一种精密数字变阻器，合成一个的编程电阻，该电阻等于参考电阻 R1 线性乘以 U1 的 Rbw/Rab。
　　以下是它的工作原理。
　　R = （Va – Vb）/IA
　　R = R1/（原始/Rbw + 1） = R1 Rbw/Rab
　　Rab = 原始 + Rbw = 通常为 5k 到 10k
　　其中 R 是编程合成电阻，R1 是参考电阻，Raw 是端子 A 和游标端子之间的电阻，Rbw 是 B 和游标端子之间的电阻，Rab 是总元件电阻。　　U1 在“分压器”（pot）模式下工作，以设置反相放大器 A2 的增益。Pot 模式使增益对 U1 的 wiper resistance （Rw） 和 Rab 不敏感。

　　将图 1 的设计方程数学运算打开，我们得到：
　　Ga2 = 原始/Rbw
　　其中 Ga2 是 A2 的增益。进一步
　　R1 两端的电压 = （Va – Vb） + Ga2（Va – Vb） = （Raw/Rbw + 1）（Va – Vb） = Rab/Rbw（Va – Vb）通过 R1 的电流 = Ia = Rab/Rbw（Va – Vb）/R1那么，由于 R = （Va – Vb）/Ia：
　　R = R1*Rbw/Rab　　Va 由 A1 的 ~10 pA 输入偏置轻负载，因此 R1 的范围可以从数百欧姆到数兆欧不等，具体取决于应用的要求。它应该是精度，当然是 1% 或更高;然后，编程和上述数学运算接管。

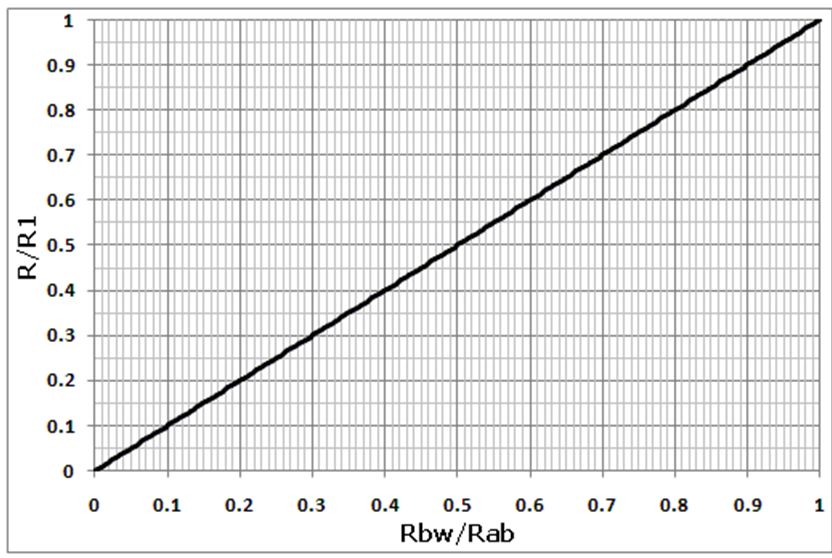
　　图 2 绘制了 R 和 Rbw 之间的线性关系。
　　图 2 R 和 Rbw 之间的线性关系显示电路合成一个的编程电阻，该电阻等于参考电阻 R1 线性乘以 U1 的 Rbw/Rab。
　　对于图 1 所示的 A2 和 U1 器件选择，可能不需要补偿电容器 （C1）。但是，如果选择更快的放大器或更高的电阻 Dpot，那么 10 pF 至 20 pF 可能是谨慎的做法。
　　同时，我认为可以公平地说，这种设计看起来与同类产品相比具有竞争力。但之前我把它描述为不完美。除了是单端拓扑（如列表中的其他两个拓扑）之外，它还在哪些方面不成为理想数字变阻器 （Digistat） 问题的完整解决方案？

　　缺点

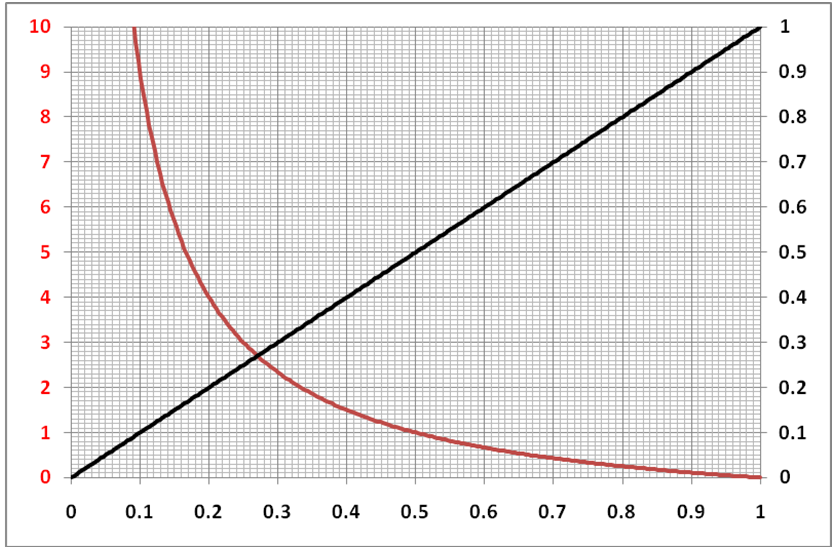
　　如图 3 所示，当 R 的编程值下降时，A2 的增益 （Ga2） 必须上升。从右到左阅读图表，我们看到增益适度上升，因为 R 从 R1 下降到 R1/4 下降了 75%，其中 Rbw/Rab = 64/256 和增益 = 3，但随后它开始起飞。这往往会夸大输入偏移、有限 GBW 和其他运算放大器非理想性等误差，同时在相对较低的信号电平下产生早期 A2 饱和的可能性。
　　图 3 Ga2（红色）和 R/R1（黑色）与 Rbw/Rab 在 x 轴上的关系图。当 R 的编程值下降时，Ga2 必须上升。
　　这些影响对设计效用的影响的严重程度，无论是轻微的、严重的还是致命的，都将取决于你需要在 R/R1 中降低多少以及应用程序的其他细节。所以，它肯定不完美，但也许它在某个地方仍然有用。
　　双端子设计
　　关于那个单一的终端问题。如果您的应用需要双端子可编程电阻，则可以考虑图 4。根据外部电路的不同，它可能不会振荡。

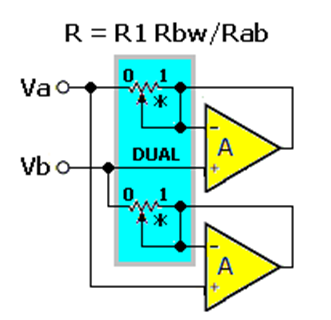　　图 4复制并交叉连接图 1 的电路，以获得双端子可编程电阻。