仪表
放大器应在其输入端提供高、平衡的阻抗 图 1 描述了一个双元件变化电桥测量系统的框图。
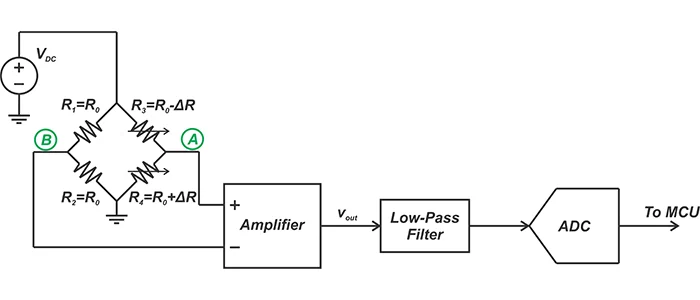
图 1 应用戴维南定理,我们可以对桥进行建模,如图 2 所示。
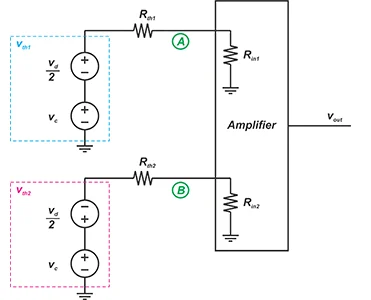
图 2
这里,\(R_{th1}\) 和 \(R_{th2}\) 是两个桥分支的等效电阻。此外,节点 A 和 B 的总戴维南等效电压 \(V_{th1}\) 和 \(V_{th2}\) 被分解为差分 (\(v_d\)) 和共模 (\(v_c\)) 分量,由下式给出:
\[v_c= \frac{v_{th1}+v_{th2}}{2}\]
\[v_d= v_{th1}-v_{th2}\] 上图模拟了 \(R_{in1}\) 和 \(R_{in2}\) 在放大器输入端“看到”的阻抗。让我们看看不相等的输入阻抗 (\(R_{in1} \neq R_{in2}\)) 如何影响电路运行。假设电桥是平衡的,电阻值如下图所示。
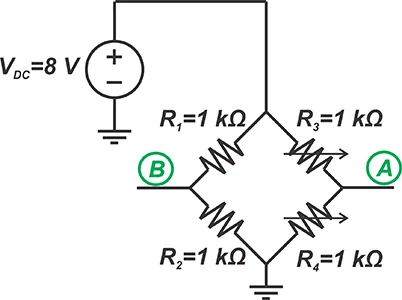
图 3
在这种情况下,戴维南等效电路的值可以找到:\(v_d\)=0, \(v_c\)=4 V, 和 \(R_{th1} =R_{th2} =500 \Omega \)。
此外,假设所使用的放大器具有不相等的输入阻抗 (\(R_{in1} \neq R_{in2}\)),我们有 \(R_{in1}=10 k \Omega\) 和 \(R_{in2}=10.5 k \Omega \)。可以得出两个重要的观察结果:
观察值 1 — 考虑图 2 中的等效模型,我们有:
\[v_A=\frac{R_{in1}}{R_{in1}+R_{th1}} v_c= \frac{10~k \Omega}{10~k \Omega + 500~\Omega} \times 4~V = 3.8095~V\]
\[v_B=\frac{R_{in2}}{R_{in2}+R_{th2}} v_c= \frac{10.5~k \Omega}{10.5~k \Omega + 500~\Omega} \times 4~V = 3.8181~V\]
虽然电桥初是平衡的(\(v_A = v_B\)),但放大器的不相等输入阻抗会对两个分支造成不相等的负载效应,并导致电桥不平衡(\(v_A \neq v_B\))。
观察 2— 假设放大器可以完全抑制任何共模信号,即 \(A_{cm}=0 \),并且差分增益为 \(A_d=20\),我们可以找到输出电压为:
\[v_{out}=A_d \times \left (v_A-v_B \right )=20 \times \left (3.8095-3.8181 \right )=-172~mV\]
虽然假设放大器具有无限的共模抑制比 (CMRR),但放大器的不平衡负载效应允许共模电压在输出端产生误差信号。如果我们使用输入阻抗较低的放大器,这种影响会更加严重。
因此,除了具有高共模抑制外,放大器还应在其输入端提供高且相等的阻抗。
差动放大器的不平衡负载效应 我们可以使用一个差动放大器,如图 4 所示,具有一些典型的电阻值,作为桥式放大器。它可以实现高 CMRR;但是,它的输入阻抗是有限且不相等的。
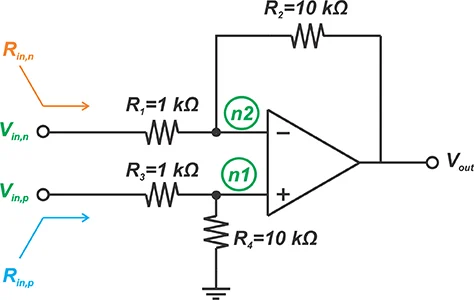
图 4
同相输入 (\(R_{in,p}\)) 的阻抗为:
\[R_{in,p}=R_3 + R_4 \]
方程 1
假设同相输入接地,反相输入的阻抗 (\(R_{in,n}\)) 可以求为:
\[R_{in,n}=R_1\]
方程 2
以图 4 中给出的电阻值,\(R_{in,n} =1~k \Omega \) 比同相输入的电阻 (\(R_{in,p}=11~k \Omega\)) 小 11 倍。 假设如图 5 所示,我们将上述差动放大器连接到我们的电桥电路。

我们能否使用公式 1 和 2 来评估差动放大器对电桥电路的负载影响?
需要注意的是,通常只有同相输入的方程有效。反相输入的公式 2 是在假设同相输入接地的情况下获得的。换句话说,反相输入的阻抗取决于施加到同相输入的电压 (\(V_{in,p}\))。这是因为 \(V_{in,p}\) 决定了出现在节点 n1 和 n2 处的电压。因此,这会影响差动放大器的反相输入吸收的电流。
一些文档,如ADI公司的“
仪表放大器设计指南”,在讨论差动放大器对桥式电路的不平衡负载影响时提到了公式1和2,但没有强调在分析桥式电路时,我们实际上不允许使用上述公式。
我相信这些文档提到公式 1 和 2 只是为了让我们了解差动放大器的不平衡负载效应。
可以证明,当任意输入施加到差动放大器时,\(R_{in,n}\) 由以下方程给出:
\[R_{in,n}= \frac {R_1}{1- \frac {R_4}{R_3+R_4} \times \frac {V_{in,p}}{V_{in,n}}}\]
其中 \(V_{in,p}\) 和 \(V_{in,n}\) 分别是放大器的反相和非反相输入端的电压。例如,使用 \( \frac{V_{in,p}}{V_{in,n}}=-1\) 和图 4 所示的电阻值,我们得到:
\[R_{in,n}= \frac{R_1(R_3+R_4)}{R_3+2R_4}=\frac{1~k\Omega \times \left ( 1~k\Omega + 10~k \Omega \right )}{1~k \Omega + 2 \times 10~k \Omega} = 523.8~\Omega\]
这几乎是公式 2 给出的值 (1 kΩ) 的一半。另一个有趣的例子是 \( \frac {V_{in,p}}{V_{in,n}}=1 \),它导致:
\[R_{in,n}= \frac {R_1}{1- \frac {R_4}{R_3+R_4}}= \frac {1~k\Omega}{1- \frac {10~k\Omega}{1~k \Omega+10~k\Omega} } =11~k \Omega\]
这等于同相输入 \(R_{in,p}\) 的电阻。在许多桥式电路中,节点 A 和 B 的电压彼此接近 (\(\frac {V_{in,p}}{V_{in,n}} \approx 1 \));因此,\(R_{in,n}\) 将接近 \(R_{in,p}\)。
换句话说,尽管差动放大器对电桥电路的两个分支的负载效应确实不相等,但 \(R_{in,n}\) 和 \(R_{in,p}\) 的差异并不像方程 1 和 2 预测的那么大。
检查差动放大器对电桥电路的负载影响
在本节中,我们将使用图 5 所示的示例电路来讨论如何计算差动放大器对桥式电路的负载影响。
图 5
我们将考虑两种不同的情况:一个是 \(R_0=1~k\Omega \) 和 \(\Delta R=0 \) 的平衡桥,另一个是 \(R_0=1~k \Omega\) 和 \(\Delta R=10~\Omega\) 的不平衡桥。
情况 1 — \(R_0=1~k \Omega \) 和 \( \Delta R=0 \) 的平衡桥
负反馈以及
运算放大器的高增益将迫使节点 n1 和 n2 处于相同的电位。由于电桥两侧的电阻值和节点电压相同,我们可以得出 \(v_A = v_B\) 的结论。
这个结果也与上一节的讨论一致:当差动放大器的反相和同相输入处于相同的电位时 (\( \frac {Vin,p}{Vin}}\approx 1\));放大器在其输入端表现出相等的电阻 (\(R_{in,n}=R_{in,p}\)),导致电桥两侧的负载效果平衡。
情况 2— \(R_0=1~k \Omega\) 和 \(\Delta R=10~\Omega\) 的不平衡桥
首先,简单的部分,同相输入的阻抗 (\(R_{in,p}\)) 是:
\[R_{in,p}=R_3+R_4=1~k\Omega + 10~k\Omega=11~k\Omega\]
因此,节点 B 的电压可以求为:
\[v_B=\frac {(R_{in,p}||1~k\Omega)}{(R_{in,p}||1~k\Omega)+1~k\Omega}\times 8~V= \frac{0.9167~k\Omega}{0.9167~k\Omega +1~k\Omega} \times 8~V=3.8261~V\]
在上面的方程中, \(R_{in,p} ||1~k\Omega \) 表示 \(R_{in,p}\) 和 \(1~k\Omega\) 的平行等效电阻。要计算 \(v_A\),我们需要找到 \(R_{in,n}\),它由下式给出:
\[R_{in,n}=\frac{R_1}{1-\frac{R_4}{R_3+R_4} \times \frac{V_{in,p}}{V_{in,n}}}= \frac {1~k\Omega}{1-\frac{10~k\Omega}{1~k\Omega + 10~k\Omega}\times \frac {V_{in,p}}{V_{in,n}}}\]
代入 \(V_{in,p}=v_B=3.8261~V\) 和 \(V_{in,n}=v_A\),我们得到:
\[R_{in,n}=\frac {1~k\Omega}{1-\frac {10}{11} \times \frac{3.8261}{v_A}}\]
方程 3
节点 A 处的电压可以找到为:
\[v_A=\frac{(R_{in,n}||1.01~k\Omega)}{(R_{in,n}||1.01~k\Omega)+ 0.99~k\Omega} \times 8~V\]
将等式 3 代入上述方程式得到 \(v_A=3.8528~V\)。 我们可以使用 LTspice 来验证这些计算。原理图如图 6 所示。如您所见,使用了 Analog Devices 的精密运算放大器 OP1177,而不是理想的运算放大器。
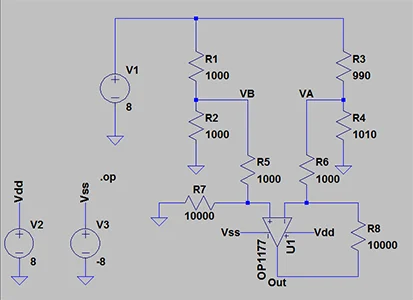
图 6
模拟得出 \(v_B=3.82609~V\) 和 \(v_A=3.85277~V\) 与我们的手牌计算一致。将 \(v_A=3.85277~V\) 的值代入方程 3 得到 \(R_{in,n}= 10.287~k\Omega\)。尽管在反相输入端“看到”的电阻小于 \(R_{in,p} = 11~k\Omega \),但差异小于方程 1 和 2 预测的差异。
这会影响线性度吗?
作为本文的一个要点,我想提请您注意一个关于电路线性度的有趣观察。
对于图 7 所示的电桥,输出由以下公式给出: \[v_{out, Bridge}=v_A-v_B=\frac{\Delta R}{2R_0}V_{DC}\]
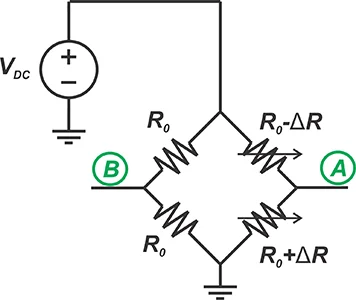
图 7
如您所见,输出与
传感器电阻值 (ΔR) 的变化呈线性关系。
上一节的讨论表明,差动放大器的负载效应随 ΔR 而变化。因此,我们可以得出结论,虽然电桥初是线性的,但连接到差动放大器的电桥的整体响应是非线性的。
为了验证这一点,我们对几个不同的 ΔR 值重复上述 LTspice 仿真。结果如图 8 所示。 在此图中,蓝色曲线绘制了放大器输出 (-Vout) 的与 ΔR 的关系。

图 8
红色曲线是穿过对应于 ΔR=0 和 ΔR=5 Ω的点的直线。
我们可以将这条线视为所需的线性响应(如果 ΔR 值较小,则预计电路不会表现出非线性行为)。从上图可以看出,实际响应逐渐偏离了我们的线性曲线。
请注意,在许多实际应用中,ΔR 可能不会像上图中那样变化那么大。该图仅试图说明电压相关负载效应如何导致非线性。
如果我们假设 ΔR 的值为 10 Ω,我们将看到放大器输出的 (-Vout) 和线性响应给出的值分别为 0.2668 V 和 0.2667 V。我们可以使用这些值来计算 ΔR=10 Ω 的终点线性误差百分比,如下所示:
\[百分比~误差=\left (\frac {V_{非线性}-V_{线性}}{V_{线性}} \right ) \times 100 \% =\frac {0.2668-0.2667}{0.2667} \times 100 \% \approx 0.04 \%\]







