两个经典振荡器电路。

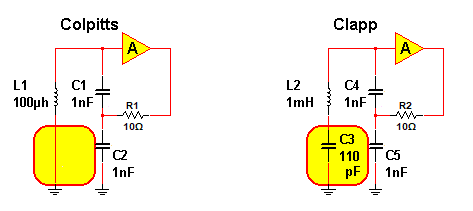
　　图 1两个经典振荡器电路：Colpitts（左）和 Clapp（右）。
　　我们之前在“科尔皮茨振荡器”和“克拉普振荡器”中分别研究过这两个振荡器。
　　然而，并排检查两个振荡器是值得花费额外时间的。
　　Clapp 振荡器是对 Colpitts 振荡器的改进，在上图中添加了一个电容器 C3。
　　放大器“A”名义上具有单位增益值，但实际上，增益值略低于该值，因为放大器实际上是“跟随器”。如果用真空管制成，则“A”是阴极跟随器。如果用双极晶体管制成，则“A”是射极跟随器。如果用场效应晶体管制成，则“A”是源极跟随器。概念本身保持不变。
　　每个振荡器都可以工作，因为 RLC 网络会在振荡频率上产生电压升压。不过，“R”并不是一个内置组件。 “R”（R1 或 R2）仅表示跟随器的输出阻抗。我们在这里看到的 10 欧姆纯粹是我的任意值猜测。其他组件也可以选择任意值，但它们是方便说明这些小动物如何工作的值。

　　我们使用 SPICE 仿真来检查两个 RLC 网络的传递函数，如图 2所示。

　　图 2使用两个 RLC 网络的传递函数进行 Colpitts 与 Clapp SPICE 模拟。
　　每个 RLC 网络的频率响应都有一个峰值，这将导致该峰值频率处的振荡。然而，克拉普电路的峰值比科尔皮茨电路的峰值更尖锐和更窄。这种变窄具有抑制以振荡频率为中心的频谱噪声的有益效果。
　　请注意，在上面的示例中，振荡峰值相差 0.16%，L1 电感器的电抗和 L2 C3 对的电抗相差 1.12%。这只是我选择了一些方便的数字的问题，目的是让两条曲线在相同的峰值频率下在这方面匹配。 （我差一点就成功了。）
　　Clapp 振荡器比 Colpitts 振荡器有几个优点。 Clapp 电路的传递函数峰值比 Colpitts 电路的传递函数峰值窄，后者往往会产生寄生偏频能量较少的振荡器输出，这意味着“更干净”的信号。
　　Clapp 电路的另一个优点是电容器 C4 和 C5 可以做得很大，因为 L2 C3 组合在振荡频率下看起来像一个非常小的电感值。较大的 C4 和 C5 值意味着“A”级输入电容的变化所带来的这些电容值的任何变化对振荡频率的影响。

　　这是因为 Clapp 电路的频率控制主要由L2 C3 对的串联谐振设置，而不是通过 Colpitts 电路中 L1 与 C1 C2 对的并联谐振来设置。如果“A”输入电容由于这样或那样的原因而变化，那么 Clapp 电路就不太容易出现如图 3所示的不需要的频移。

　　图 3 Clapp 与 Colpitts 频移比较显示 Clapp 电路（右）如何不易出现这种不必要的频率偏移。