适用于音频应用的压控滤波器
压控滤波器（或 VCF）是模拟合成器的支柱。常见的配置可以说是使用基于运算跨导放大器 (OTA) 的滤波器，其中 LM13600 和 LM3080 等 IC 是流行的选择。 Korg 制造了诸如 Korg35 之类的芯片，基于巧妙的Sallen-Key布置或 OTA，具体取决于制造时间，而 ARP 制造了 4023、4035 和 4075 模块，这些模块利用了 OTA、Moog 拓扑，和电流反馈运算放大器。
但有一个过滤器比其他过滤器更胜一筹，因为它富有创意、有效，而且（我有充分的权威）听上去“才华横溢”。这就是穆格梯形滤波器。
穆格阶梯滤波器原理图
言归正传，让我们看一下穆格过滤器，大致与穆格 Prodigy 中出现的一样。
图 1. 的 Moog 滤波器，它出现在 Moog Prodigy 模拟合成器中。
我们在这里看到“梯子”中的八个晶体管，通过电阻分压器链偏置，由偏置/控制电流Ibias驱动。音频输入施加到 Q1，反馈（用于谐振，也称为电子音乐中的强调）施加到 Q2，其他晶体管成对连接在基极，电容器并联其发射极。输出被视为顶部电容器两端的电压。为了稍微简化一下，我们可以（小心地）移除偏置组件，得到如图 2 所示的原理图。
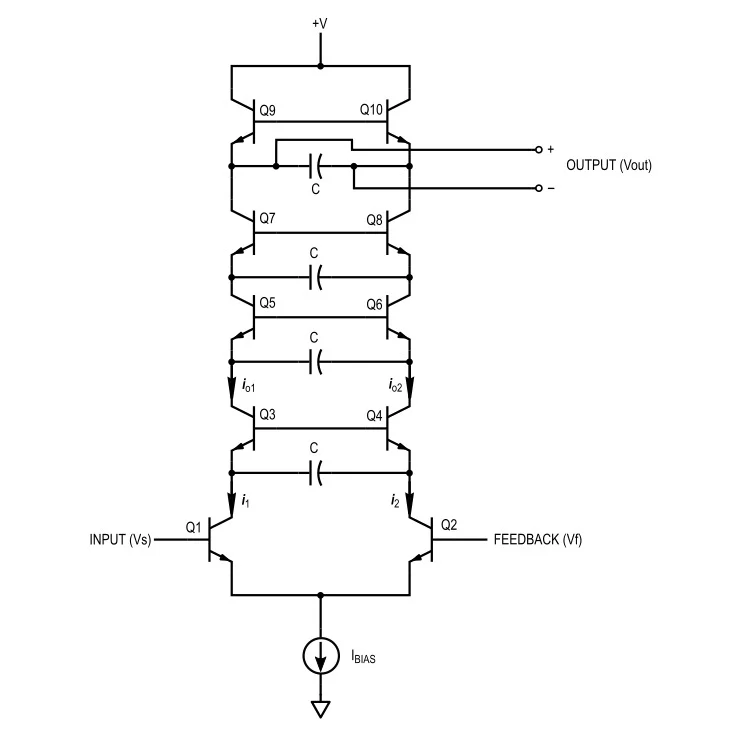
图 2. Moog 滤波器的简化原理图
这只是有点误导，因为当然基极不是浮动的，而是通过分压器保持恒定电位。
穆格阶梯滤波器解释
我们只看一下电路。电路的截止频率控制是施加到差分对 Q1-Q2 的电流Ibias。改变Ibias会导致整个网络的晶体管偏置电流发生变化。忽略基极电流（即假设高 beta），我们看到无论流过 Q1 的直流电流都必须流过左侧梯子的其余部分，对于 Q2 和右侧梯子也是如此。
晶体管对Q3-Q4、Q5-Q6和Q7-Q8各具有两个晶体管和一个电容器。一对晶体管共享相同的基极电压，但具有不同的发射极电流。由于小信号电流不同，晶体管的小信号v be也会不同，因此发射极电容器上会产生电势。电容器是一种与频率相关的电抗，可产生滤波效应。
无论如何，这就是这个想法。为了了解其准确性，我们必须分析滤波器的三个不同部分，如图 3 所示。
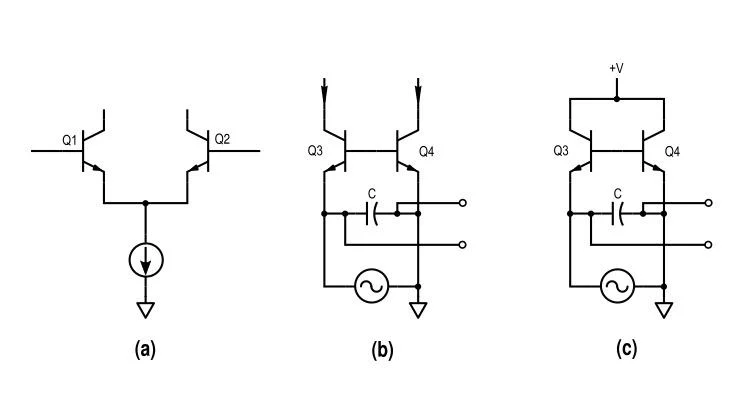
图 3. 梯形滤波器拓扑的三个要素。 (a) 驱动差分对。 (b) 中阶梯低通滤波器部分。 (c) 顶层的输出滤波器部分。
该电路可分为驱动器（图 3a）和低通滤波器（图 3b 和 3c）。 (b)和(c)的输入源是电流信号，在反馈侧接地以便于分析（读者可以通过对称性确认这是安全的）。
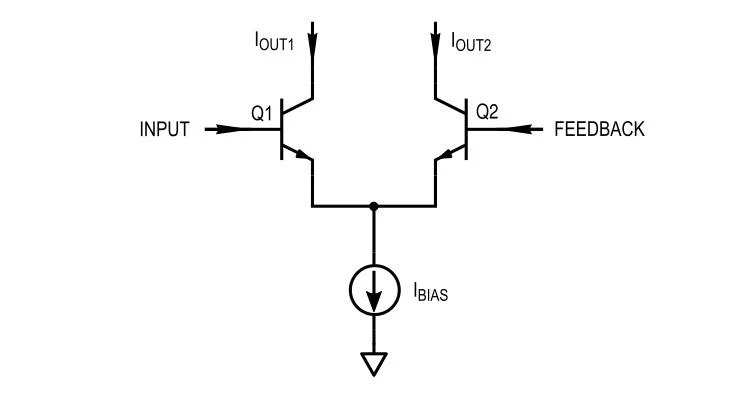
图 4. 滤波器的驱动部分。
驱动部分是差分对，也称为发射极耦合对。为了从小信号的角度分析该电路，我们可以用适当的音频有源区域模型替换晶体管。两种常见的选择是混合 pi 模型（使用输入电阻建模的跨导）或 T 模型（使用基极发射极电阻建模的跨导）。
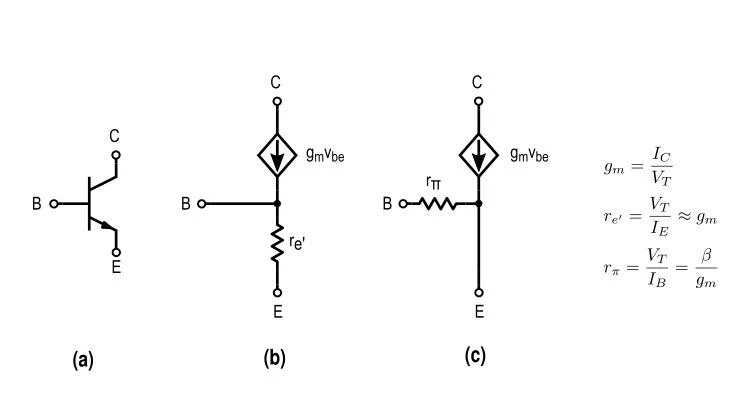
图 5. 三个晶体管模型。 (a) NPN 晶体管。 (b) T 模型。 (c) 混合 pi 模型。
T 模型和混合 pi 模型中的电阻通过等于晶体管 beta 的系数相关。尽管它们具有不同的电路配置，但模型在分析上是相同的。对于驱动电路，我们可以使用混合圆周率模型。
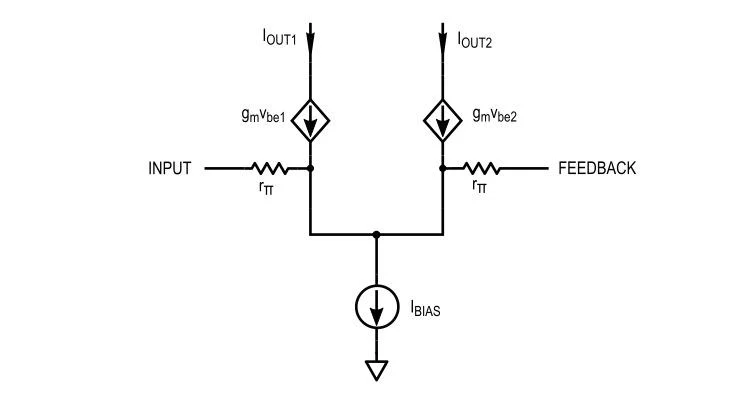
图 6. 我们可以使用晶体管的低频混合 pi 等效项对驱动器中的晶体管进行建模。
通过用开路替换恒流源和用接地连接替换恒压源，可以简化电路，如图 7 所示。对于小信号电流增益计算，负载被短路，使我们能够有效地将集电极接地。
通常，我们还会计算输出阻抗以考虑负载，但在这种情况下，我们不必这样做。这可以通过相关电流源的存在来证明，并且因为我们没有考虑早期效应（它会显示为与电流源并联的输出阻抗）。我们不会考虑共模效应，因为晶体管的偏置点足够小。
，为了对差分输入进行建模，我们将对两个晶体管施加相等且相反的输入电压。这并不是必要的，但它会使分析更容易。
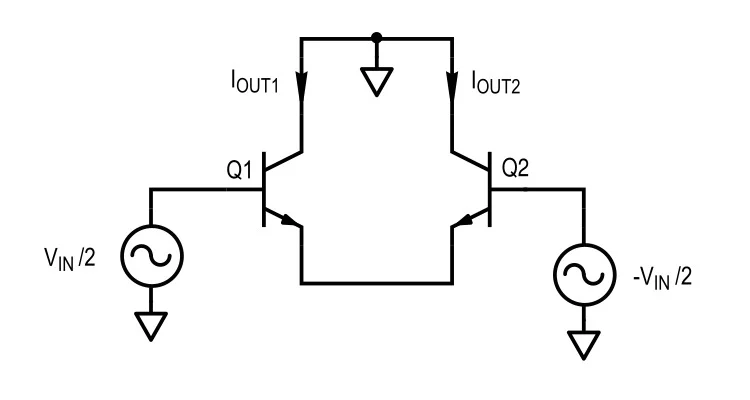
图 7. 使用一些简化技术进行分析的小信号电路。
这里可能不明显的是晶体管发射极将处于固定电位（交流接地）。这是由于电路的对称性造成的。
本质上，Q1 驱动的任何交流电流都将流过 Q2，并且 pi 模型基极电阻不会有任何相关电流流过它们。不会发生电压变化，因此我们可以安全地将发射器接地。
这给我们提供了如图 8 (a) 所示的电路。请注意，由于接地，电路的两半可以单独分析，如 (b) 中的晶体管 pi 模型所示。
图8。 (a) 用于分析的终小信号电路，(b) 差分电路的一侧，即“半电路”。
驱动电流由下式给出
$$I_{OUT1} = -I_{OUT2} = g_m v_{be1} = \frac{g_m v_{in}}{2}$$
其中v in是驱动级输入的总差分小信号电压。在没有反馈的情况下，这等于滤波器输入。
总之，驱动器部分由一对差分晶体管组成，为梯形电路提供差分输入电流。该输入电流取决于 gm，因此也取决于晶体管的偏置电流和温度。
