模拟混音器
　　可以设计一个接受两个模拟输入并产生与输入的乘积相对应的输出信号的电路。它们是围绕二极管或晶体管构建的，并利用这些设备固有特性的乘法关系。我将这些设备称为“模拟”混频器，以强调乘法不涉及数字切换操作的事实。
　　这种模拟混音方法非常直观。不幸的是，现代射频接收器经常采用远不直观的数字/开关方法作为降低功耗的手段。模拟混频器绝不是无用的，基于二极管的版本在甚高频系统中很有价值，在这些系统中，BJT 和 FET 所表现出的不可避免的带宽限制会损害性能。尽管如此，“数字”下变频混频器——或“开关”混频器，或（在某些实现中）“电流换向”混频器——广泛应用于当今的射频系统中，因此了解它们是什么以及它们如何工作。
　　切换混音器

　　开关混频器提出的个概念障碍是本地振荡器 (LO) 信号。它是方波（或者，如果它是正弦波，则混频器将其视为方波）。就我而言，这是不可原谅的。在我的世界观中，射频是模拟电子学的点——随处可见的正弦波、老式的数学关系……甚至数字数据也是使用模拟波形来传输的。一旦您接受了这种开关混频器业务允许笨重的数字信号进入平滑变化的射频世界的事实，您就必须面对这样一个事实：开/关切换是一种乘法形式。

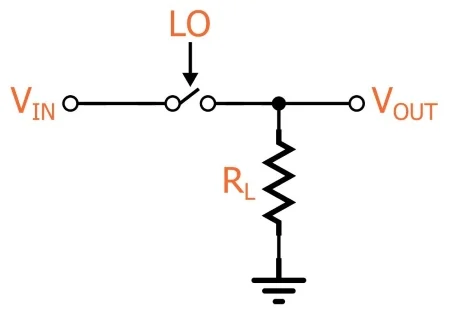
　　事实上，这只不过是一个电压控制开关。接收到的 RF 信号用作输入电压，LO 控制开关。所以我们在这里真正要做的就是根据 LO 的频率打开和关闭输入信号。
　　我知道你问的个问题是：“这怎么可能是混合的？”好吧，首先记住混合是乘法。如果将 LO 视为在 0 V 和 1 V 之间转换的方波，则开关实际上将输入信号乘以 LO：当开关闭合时，输出等于输入乘以 1。当开关打开时，输出等于输入乘以零。
　　下一个问题：“这怎么可能等于乘以正弦曲线？当然，频率可能是相同的，但表明乘法产生频率转换的数学关系是基于两个正弦波，而不是一个正弦波和一个方波。”很好的一点，但是您忘记了一件事：正弦波位于方波内部。傅里叶已经告诉我们了，我们不敢怀疑他。我们看不到它，因为它无可救药地与所有谐波分量混合在一起，但它就在那里某处，这意味着以下内容：如果此开关装置将输入信号乘以 LO 方波，那么它也会将输入信号相乘频率等于 LO 频率的正弦信号。
　　此时，您可能想知道为什么我们想要用所有这些谐波分量来搞乱乘法，但是谐波能量可以通过滤波来抑制，而且事实证明，在许多情况下，谐波的问题比基于模拟混频器的解决方案。
　　这真的有效吗？

　　让我们看一个例子。这是 LTspice 电路：

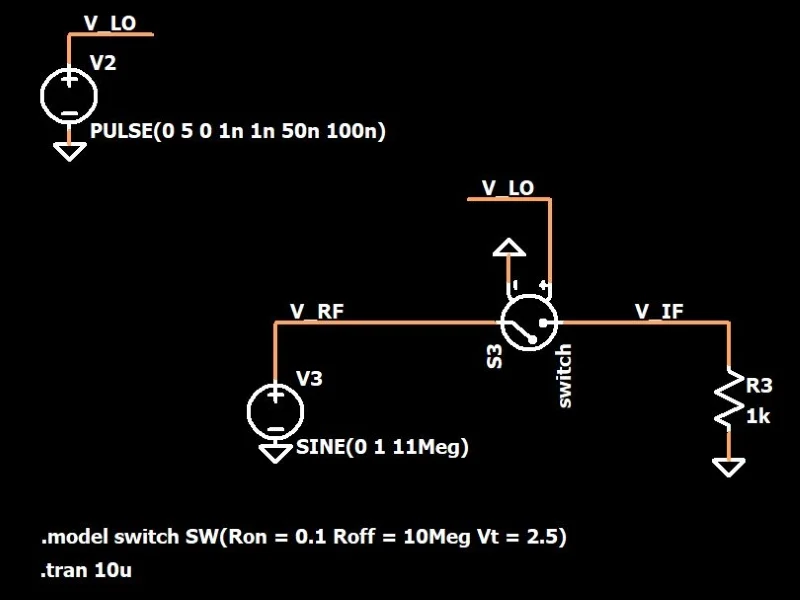
　　让我们想象一下，该混频器正在将接收到的射频信号下移至中频 (IF)。接收到的信号为 11 MHz，LO 为 10 MHz 方波。乘法是通过连接到 LO 信号的压控开关来实现的。输出信号的频率应等于输入频率减去LO频率，即1 MHz。

　　让我们看一下一些波形。个图显示了输入信号和 LO。

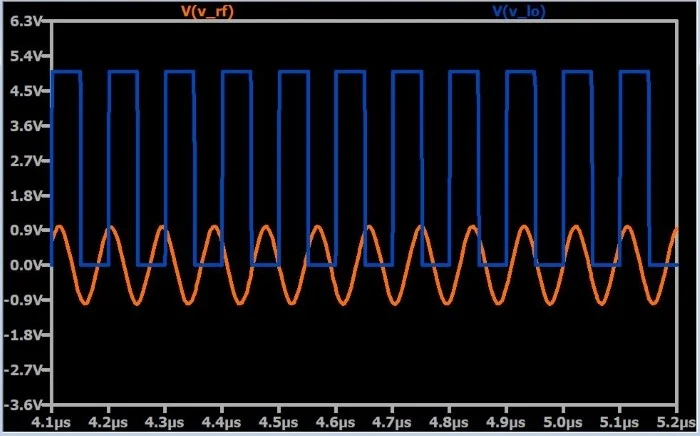
　　这是相同的图，但输出包含在单独的窗格中。

　　您可以在这里看到乘法关系，但到目前为止，看起来我们所做的只是破解了一个完美的正弦波。不过，当你缩小时，图片开始出现：

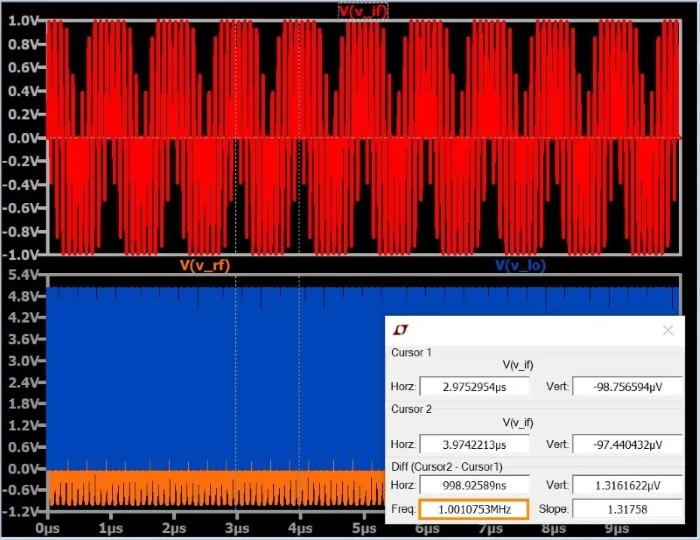
　　您可以看到，所有这些黑客行为都以某种方式导致了一些看起来模糊的正弦曲线，而这个模糊的正弦曲线恰好具有 1 MHz 的频率。我们的终确认来自FFT，它显示了 1 MHz 处的主导尖峰（以及大量谐波内容）：

　　结论
　　混频器电路是一个广泛的主题，本文只不过是介绍基于开关的混音的基本概念。尽管如此，我们必须从某个地方开始，实际上您可以通过使用CMOS 传输门代替理想化的压控开关来实现上述电路，从而创建一个真正的混频器。