是什么导致放大器不稳定？
只要环路增益在任何重要的频率下都不会变成正反馈，闭环系统就是稳定的。环路增益是一个相量（这意味着它同时具有幅度和 相位属性）；不稳定的常见原因是环路周围的额外相移，将完美的负反馈转变为正反馈。环路增益相位“重要”的频率是指环路增益为 0dB 或以上的频率。
查看图 1中所示的放大器电路，可以通过确定信号绕环路一周且环路损坏时遇到的相移来估计其稳定性。以下示例演示了一种通过使用仿真软件 Op Amp Macromodel 并采用 Pspice 中提供的理想组件来实现此目的的方法。
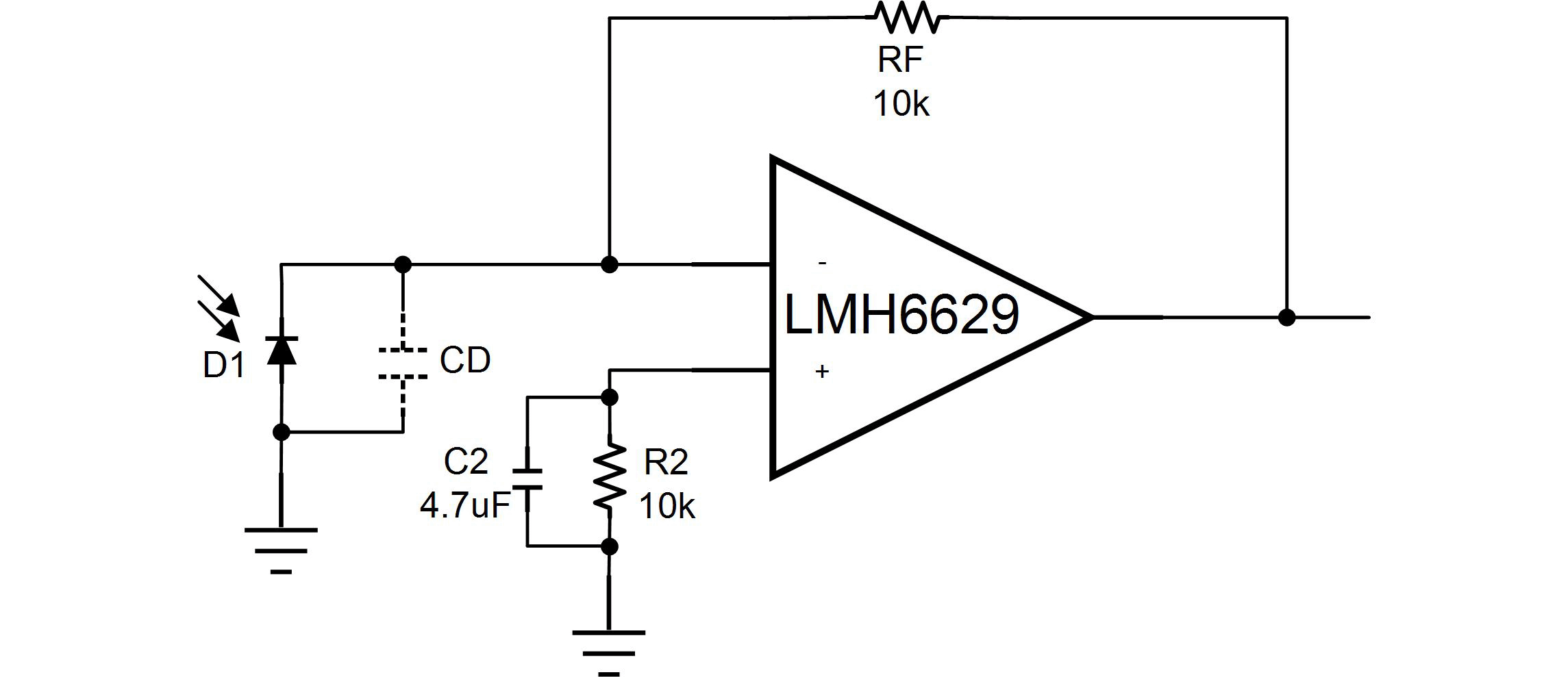
图1：跨阻放大器
高速低噪声跨阻放大器 (TIA) 稳定性示例：
让我们以跨阻放大器 (TIA) 为例，探讨其稳定性，以演示我们即将提出的技术。 TIA 有许多工业和消费用途，例如 LIDAR（光检测和测距）、条形码扫描仪、工厂自动化等。设计人员面临的一些挑战是限度地提高 SNR 并实现传递预期信号所需的速度/带宽没有衰减或退化。
图 1 是使用 LMH6629 的此类设计，LMH6629 是一款超高速 (GBWP= 4GHz) 低噪声器件 (0.69nV/rtHz)，稳定增益为 +10V/V（COMP 引脚连接到 VCC）。 LMH6629 的补偿 (COMP) 输入可连接至 VEE，以将稳定增益降低至 4V/V。为了获得转换速率和带宽（小信号和大信号），在此示例中，COMP 引脚连接到 VCC。可达到的带宽与放大器 GBWP 直接相关，与跨阻增益 (R F ) 和光电二极管固有寄生电容成反比。
决定给定放大器使用什么反馈电阻 (R F )的一种便捷方法是参考图 2的图，其中绘制了 使用 LMH6629 时的总等效输入电流噪声密度“i ni ”与 R F 的关系。在此图中，“i n ”是 LMH6629 输入噪声电流，“en ”是 LMH6629 输入噪声电压，“k”是玻尔兹曼常数，“T”是温度（单位：°C）。
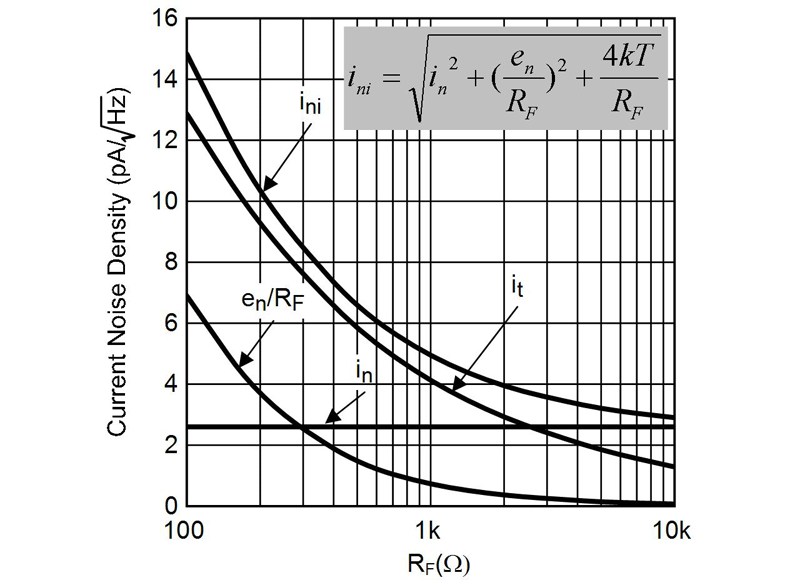
图2：总等效噪声密度与反馈电阻
从图 2 中可以明显看出，对于 LMH6629，将 R F设置 为 10k W 可确保的总等效输入电流噪声密度 i ni，从而获得的 SNR。 R F的任何进一步增加都会降低可达到的速度，并且 SNR 没有明显的改善。
对于看似简单的电路来说，使稳定性分析变得复杂的一个主要因素是寄生元件的影响。在图 1 的电路中，几乎没有任何迹象表明该电路可能接近不稳定。所示的寄生分量“C D ”是光电二极管固有电容，其根据光电二极管面积及其灵敏度而缩放。 R2 用于消除 LMH6629 输入偏置电流引起的失调误差，C2 则消除 R2 的噪声。
假设光电二极管标称电容 (CD )为 10pF，图 1 电路的模拟响应如图 3所示 ，表明该电路不稳定；频率响应中的大而尖锐的峰值可以明显看出这一点。在频域中，可以通过了解电路的相位裕度 (PM) 来确定稳定性。出于仿真目的，光电二极管的简化等效电路是电流源。
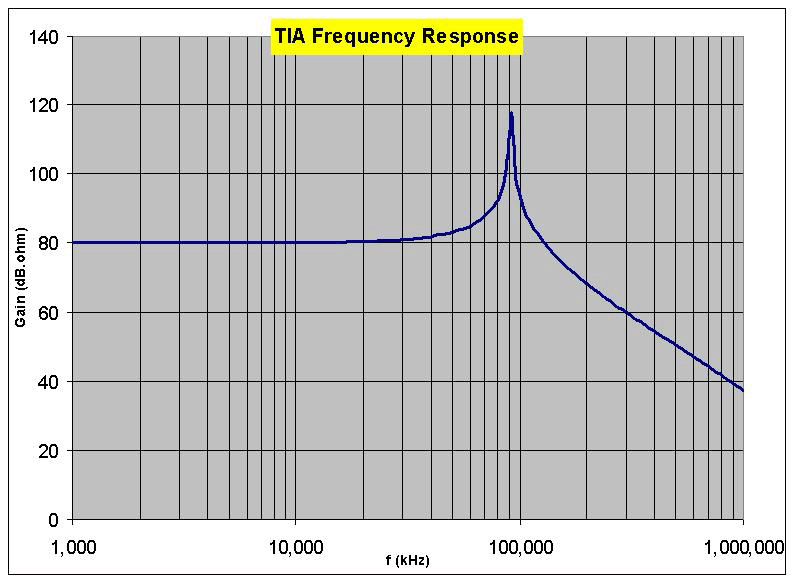
图3 ：TIA 频率响应表明不稳定
对于有经验的用户来说，相对较大的反馈电阻 R F缺乏稳定性可能证明 R F “查看”反相运算放大器输入的寄生电容是振铃和过冲的原因。这可以称为环路“过度相移”。反相输入寄生电容由光电二极管电容和LMH6629的输入电容组成。 LMH6629 的宽带宽降低了足以导致过度相移的总输入电容，从而加剧了问题。纠正这种情况有效的方法是在R F两端插入一个适当值的电容器 (C F ) 。
除非进行全面的笔式分析来寻找导致这种行为的低相位裕度的原因，否则在选择补偿元件以提高稳定性时除了反复试验之外别无选择。一种比笔划方法快得多的更严格的方法是使用仿真来更深入地了解环路行为随频率的变化，而无需复杂算术的麻烦和计算错误的可能性。
所需要的是能够观察“开环”配置中的电路，以便研究环路增益 (LG) 幅度和相位。仿真提供了实现这一目标的机会，因为它为用户提供了各种可以有效完成工作的理想组件。
在图 4的仿真电路中，环路已在 AC 方面打开（其中相位裕度很重要），同时保留 DC 闭环，以便正确建立工作点。这是通过输出端的大值串联电感 (L1) 和大值并联电容器 (C1) 来实现的。
图4 ：插入大“L”和大“C”以在 AC 下开环进行仿真
驱动大电容器 (V_Drive) 的交流源可设置为 1V，器件输出处的模拟响应是 LG 函数，如图5所示。图 5 中约 0° 的低相位裕度证实了过度的闭环频率响应峰值如图 3 所示。使用的品质因数是相位裕度应大于 45° 以确保稳定性。
笔记：
1. 在开始频率响应仿真之前，确保输入电流源（代替光电二极管）设置为“AC 0”
2. 显示的结果是 C F 设置为 0pF 时的结果
3. 图5中实线表示幅度，虚线表示相位角
4. 相位裕度是“LG函数”跨越0dB时的相位角
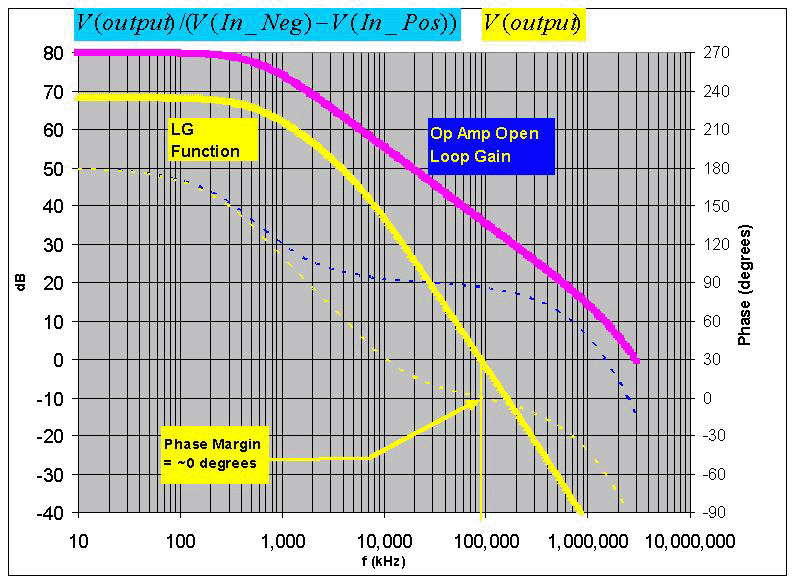
图5 ：开环图显示相位裕度不足
为了找到适当的补偿电容器值以提高相位裕度，可以将各种 C F值 （在图 4 的电路中）的噪声增益与 LMH6629 开环增益图一起绘制出来，如图6所示。噪声增益为 V(Drive)/V(In_Neg)。注意LG模拟的低频值高于0dB；这是因为 LMH6629 的宏模型还对其差分输入电阻进行建模。
大多数 Pspice 模拟器允许使用图 6 中所示的“.STEP PARAM”语句来运行多个模拟并显示所有叠加的结果。其他模拟器可能具有专用命令来允许这种类型的同时模拟。 C F 值是在噪声增益函数上放置一个极点，该极点与 LMH6629 的开环增益图相交的频率。从图 6 中可以看出，本例中的C F = 0.25pF。
任何较高的 C F 值都会产生带宽损失，任何较低的值都会没有足够的相位裕度。如果 C F 足够高（例如本例中为 7pF），噪声增益图可能会截取开环图低于 20dB，这是 LMH6629 的稳定增益；这种情况将再次不稳定，或者放大器可能具有过度的频率响应峰值。因此，存在一个稳定区域和一个值。
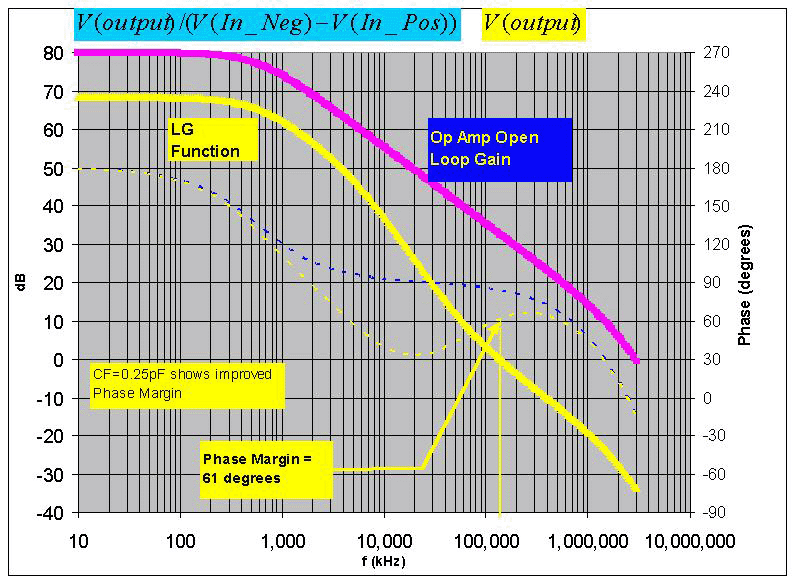
图6 ：C F 优化的噪声增益图
图 7显示了当 C F =0.25pF时 LG 作为频率函数的结果图，以确认相位裕度已从没有 C F 的原始 0° 增加到 61° 。
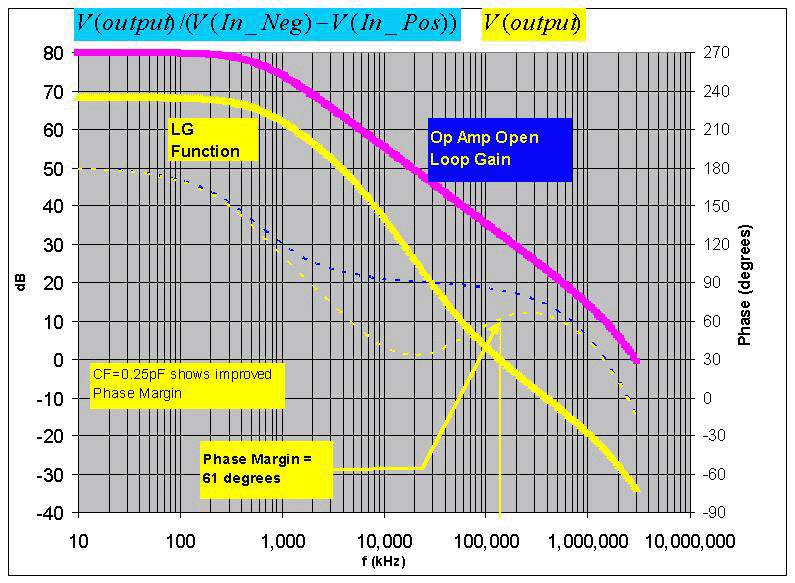
图7 ：确认 C F带来的相位裕度改善的开环图
找到 C F的值后，可以返回到原始闭环配置（没有添加用于研究 LG 和 NG 的大 L 和 C）并获得具有 C F 值（在此为 0.25pF）的阶跃响应。情况）包括在内。图 8是各种 C F 的图， 以确认较大或较小的 C F 值可能不稳定，或者可能具有较长的振铃和稳定时间，而 C F 会产生良好的阶跃响应且振铃。
显然，0pF和7pF是完全不稳定的。并不是说 7pF 的振荡频率比 0pF 的振荡频率高很多，因为噪声增益和放大器开环增益图之间的截距频率较高，如图 6 所预测。
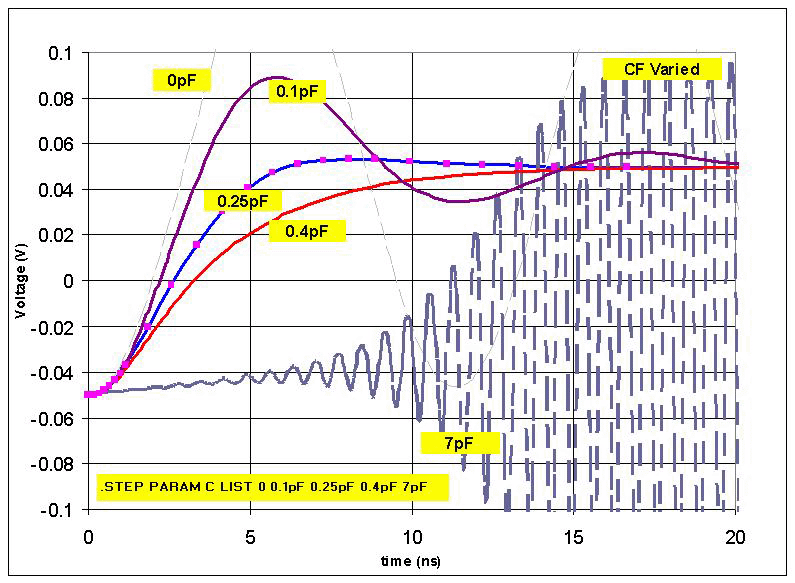
图8 ：各种 C F的闭环阶跃响应
