在本文中，我们将展示如何实现更高的直流精度。

　　随着我们的进展，我们将参考第 1 部分，特别是图 1 的框图。

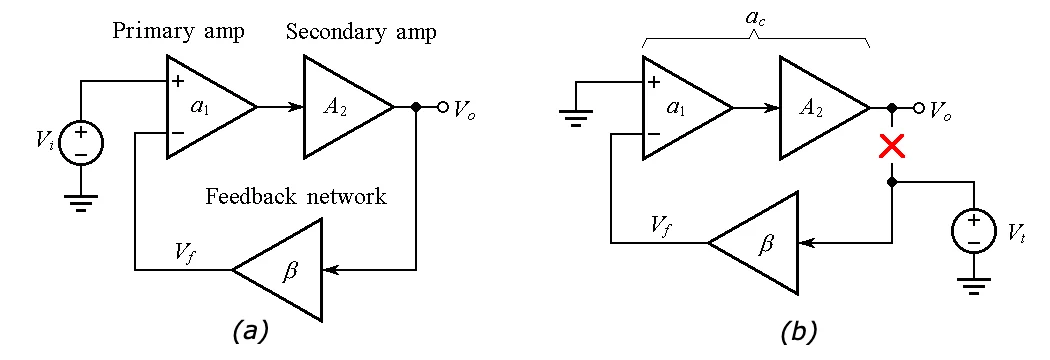
　　图 1.  (a) 复合电压放大器的框图。 (b) 求出 复合放大器的开环增益 a c和噪声增益 1/β 的电路。

　　我们还将参考图 2 中总结的闭合率 (ROC)可能性。

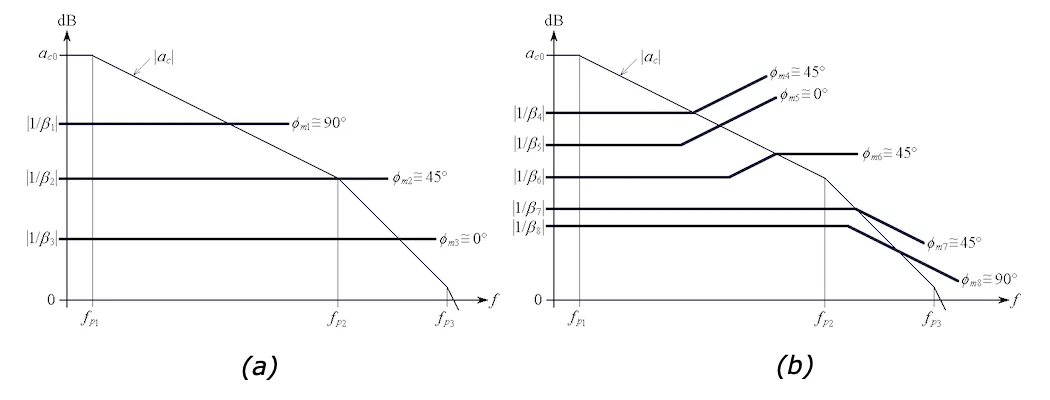
　　图 2.  (a) 经常遇到的相位裕度情况，其中 (b) 与频率无关的噪声增益 1/β(jf) 和 (b) 与频率相关的噪声增益 1/β(jf)。
　　环路增益和直流精度之间的相关性
　　让我们考虑一下下面的图 3，它显示了流行的同相运算放大器配置及其相应的开环增益、噪声增益和环路增益的波特图。

　　同相运算放大器电路配置和波特图

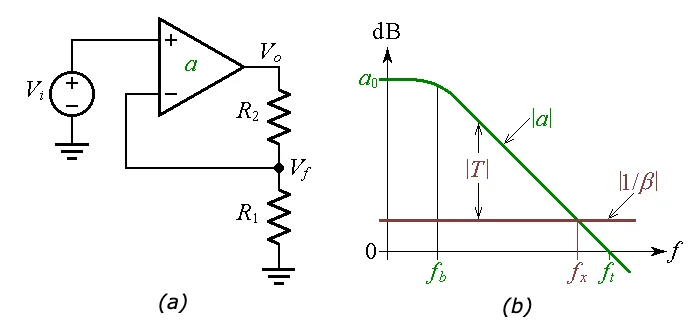
　　图 3.  (a) 同相运算放大器配置。 (b) 伯德图显示了开环增益 a、噪声增益 1/β 和环路增益 T。
　　注意，a 0是增益a的DC值，f b是带宽，ft是过渡频率。 | 的频率一个|和|1/ β |相交称为交叉频率 f x。
　　在图 3(a) 中，我们看到  同相运算放大器的闭环增益 A ，其形式具有深刻的意义
　　\[A = \frac {V_o}{V_1} = A_{理想} \frac {1}{1+1/T}\]
　　公式1
　　在哪里
　　\[A_{理想} = \lim_{T\rightarrow \infty} A = 1+ \frac {R_2}{R_1}\]
　　公式2
　　此外，T称为环路增益，并且
　　\[T = a\beta\]
　　公式3
　　其中a称为开环增益，β称为反馈因子
　　\[\beta = \frac {V_f}{V_o} = \frac {R_1}{R_1+R_2}\]
　　公式4
　　反馈因子的倒数
　　\[\frac {1}{\beta} = 1 + \frac {R_2}{R_1}\]
　　公式5
　　称为噪声增益，因为这是运算放大器放大任何输入噪声（例如输入失调电压 \(V_{OS}\)）的增益。显然，对于当前电路，我们有 \(A_{ideal} = 1/\beta \)。
　　将方程 3 重写为T = aβ = a/(1/β)，两边取对数，然后乘以 20 以分贝表示，表明我们可以可视化 | 的分贝图。T |作为| 的分贝图之间的差异一个|和 | 的分贝图1/β |。如图 3(b) 所示。
　　参考方程 1，很明显，术语 1/ T代表一种形式的误差：在我们努力近似方程 2 的理想增益时，我们希望T尽可能大：理想情况下，T → ∞ ，所以A → \(A_{理想}\)。
　　在高噪声增益下实现高直流精度
　　如图3(b)所示，噪声增益越大，环路增益越小，精度越低。
　　如果当前的应用需要高噪声增益和高直流精度怎么办？
　　例如，假设我们希望使用 \(a_0\) = 100,000 V/V (= 100 dB) 的运算放大器实现 \(A_{ideal}\) = 1,000 V/V (= 60 dB) 的同相放大器）。这将给出 \(T_0\) = 100 – 60 = 40 dB 的直流环路增益，或 \(T_0\) = 100，根据公式 1 表明直流误差约为 1%。
　　如果我们想显着减少这个误差怎么办？
　　显然，单个运算放大器无法做到这一点，因此让我们级联其中两个运算放大器，如图 4(a) 所示。

　　级联两个运算放大器的电路和随附的波特图可视化

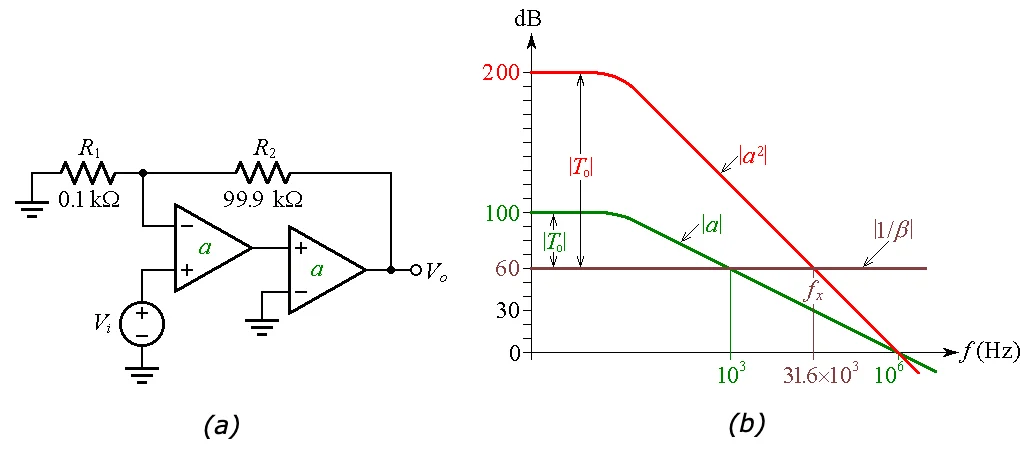
　　图 4.  (a) 级联两个运算放大器以实现 a×a = a 2的复合开环增益。 (b) 波特图可视化。交叉频率从10 3 Hz 变为f x = (10 3 ×10 6 ) 1/2 = 31.6×10 3 Hz。
　　随后的复合放大器将具有开环增益 \(a \times a = a^2\)，我们通过将a的幅度加倍来逐点构建其幅度图。
　　如图 4(b) 所示，对于百万分之 0.1 的直流误差，我们现在有 \(T_0\) = 200 – 60 = 140 dB，或 \(T_0 = 10^7\)，改进。不幸的是，我们为此付出的代价是彻底的不稳定！
　　事实上，虽然单运放电路符合图 2(a) 的 \(|1/\beta_1|\) 曲线，但对于 \(\phi_m \approx 90^\circ \) 的相位裕度，复合器件??符合图2(a)的\(|1/\beta_3|\)曲线，其中\(\phi_m \approx 0^\circ \)。
　　显然，我们的复合材料需要频率补偿。
　　频率补偿
　　由于缺乏修改\(|a^2|\)曲线的能力，我们必须集中精力适当修改|1/β|曲线。
　　常见的策略是瞄准 \(\phi_m = 45^\circ \)，与图 2(b) 的 \( |1/ \beta_7| \) 曲线一致。我们通过将合适的电容 \(C_f\) 与 \(R_2\) 并联来实现这一点，如图 5(a) 所示。虽然在低频下保持 \(|1/ \beta | \) 曲线不变，但 \(C_f\) 的存在在频率处引入了一个断点，在该频率处 \(C_f\) 呈现的阻抗在幅度上等于 \ (R_2\)。
　　对于 \(\phi_m = 45^\circ \)，我们希望该频率为交叉频率 \(f_x\)，因此我们施加 \(|1/(j2\pi f_x C_f)| = R_2 \) 并得到
　　\[C_f = \frac {1}{2 \pi f_x R_2}\]
　　公式6
　　根据图 5 中的 \(R_2\) 和 \(f_x\) 值，我们得到 \(C_f\) = 50.38 pF。将复合放大器的闭环增益表示为\(A_c\)，我们观察到除了直流精度的显着提高之外，我们还实现了从1 kHz到31.6 kHz的闭环带宽扩展。

　　复合放大器的频率补偿

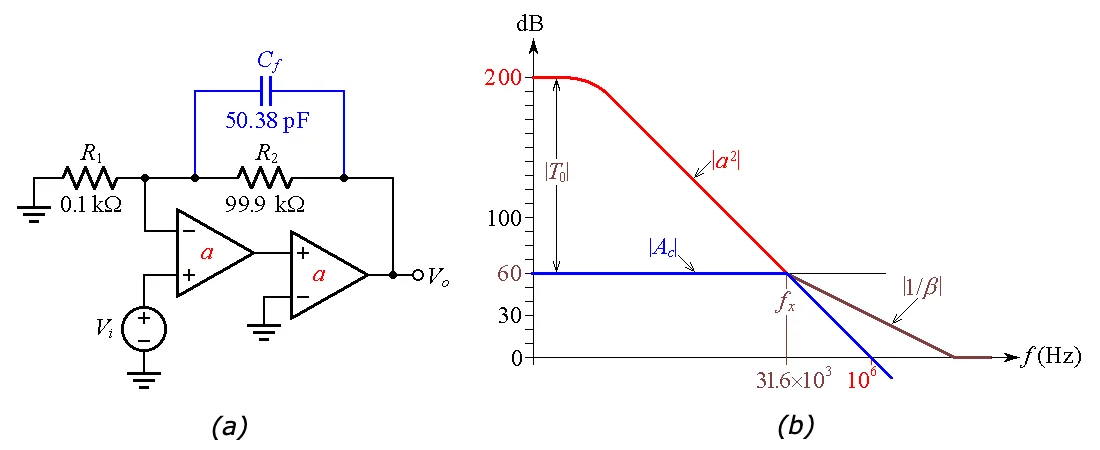
　　图 5. 图 4 复合放大器在  m = 45° 时的频率补偿。
　　已补偿 \(\phi_m = 45^\circ \) 的放大器的闭环交流响应表现出峰值。如果不希望出现峰值，我们可以补偿 \(\phi_m = 65^\circ \)，它标志着峰值的开始。
　　这要求我们适当降低断点频率，现在在图 6(b) 中表示为 \(f_1\)。

　　频率补偿 φ-sub-m > 45°

　　图 6.  m > 45°的频率补偿。
　　我们如何找到必要的\(f_1\)
　　考虑到 \(a^2\) 增益贡献 –180°，\(\phi_m\) 将与 \(f_1\) 在 \(f_x\) 处的相位贡献一致，或者
　　\[\phi_m = tan^{-1}\frac {f_x}{f_1}\]
　　公式 7
　　应用简单的几何推理，我们注意到 \(f_0\) 是 \(f_1\) 和 \(f_x\) 的几何平均值，或者
　　\[f_0 = (f_1 \乘以f_x)^{1/2}\]
　　公式8
　　消除 \(f_x\)，我们发现，经过较小的代数运算后，
　　\[f_1 = \frac {f_0}{\sqrt{tan \phi_m}}\]
　　公式 9
　　因此，对于 \(\phi_m = 65^\circ \)，我们的电路需要 \(f_1\) = 21.58 kHz，这是通过将图 5(a) 的 \(C_f \) 提高 31.62/ 来实现的21.58 以获得图 6(a) 所示的 73.78 pF 值。
　　使用 PSpice 仿真进行验证
　　我们可以通过计算机模拟很容易地验证上面进行的计算。图 7 的 PSpice 电路已设置为模拟 \(\phi_m\) = 0°、45° 和 65° 的情况。当 \(\phi_m\) = 0° 时，电路表现出几乎无限的峰值，表明电路处于振荡边缘。

　　（当使用现实生活中的组件实现时，由于我们的简化运算放大器模型中未考虑高阶极点频率而导致额外的相位滞后，因此电路肯定会振荡。）

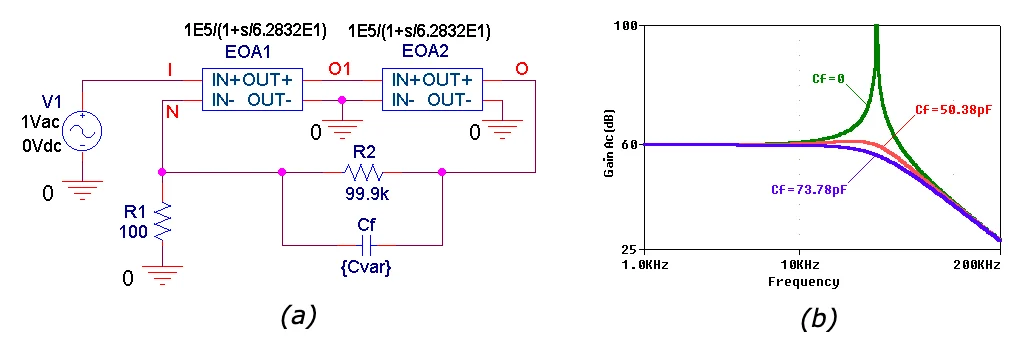
　　高精度直流精度复合放大器的 PSpice 电路和闭环交流增益
　　图 7.  (a) 使用拉普拉斯模块模拟 1 MHz 运算放大器的高精度 DC 精度、60 dB 增益复合放大器的 PSpice 电路。 (b) 相位裕度约为 0°、45° 和 65° 的闭环交流增益。
　　对应于\(\phi_m ? 45^\circ \)的闭环增益表现出\(f_B = 40.3 kHz \)的带宽，而\(\phi_m ? 65^\circ \)我们有\(f_B = 30.5 kHz\）。如果需要较低的带宽（例如为了降低噪声），可以增加\(C_f\)，但只能增加到一定程度。
　　增加 \(C_f\) 会改变 |1/β|图 6(b) 的曲线进一步向左移动，使其水平轴断点更接近交叉点。如果这个断点移到交叉频率的左侧，我们会再次遇到 \(\phi_m ? 0^\circ \) 并且电路将处于振荡的边缘。