运算放大器简介
运算放大器(通常称为运算放大器)是设计
电子电路的普遍构建模块。如今,这些设备被制造为小型
集成电路,但这个概念很久以前就开始使用真空管。 1946 年有一项早期使用运算放大器概念的(参考文献 1),尽管当时并未使用该名称。人们通常认为 Raggazinni 在 1947 年创造了“运算放大器”一词(参考文献 2)。
早在 20 世纪,我在参加大学模拟计算实验课程时就接触过运算放大器。模拟电路用于通过复杂的
接线板连接求和放大器、微分器和积分器来模拟系统。模拟计算的使用正在逐渐消失,被数字计算机所取代,所以我不能说我从课程的计算部分中学到了很多。不过,我确实学到了很多关于运算放大器电路和控制系统的知识,这些知识在今天仍然很有价值。
理想运算放大器
为了理解运算放大器的基本功能,我们使用“理想运算放大器”的概念。理想的运算放大器是压控电压源,如图 1所示,具有以下属性:
无限增益 (A v ) 和无限带宽
零输出阻抗 无限输入阻抗(零输入电流)

理想运算放大器电路原理图。图 1理想的运算放大器是一个具有无限输入阻抗和零输出阻抗的压控电压源。
通常包括一个重要的第四个属性,但它仅在运算放大器施加负反馈时才有效:
两个输入之间零伏
如果您想知道该运算放大器如何获得电源,该器件有两个电源连接(正极和负极),在讨论电路设计时经常被忽略(但在连接实际电路时重要)。通常,提供双极电源,+/-15V,支持健康的信号摆幅。
运算放大器酷的一点是,对于许多非关键应用来说,运算放大器的性能(增益、带宽、阻抗等)与电路要求相比非常好,以至于它们确实像理想的运算放大器一样工作。它们易于设计,并已成为电子系统的重要构建模块。
运算放大器配置和原理图
同相放大器 我们将看到的个常见运算放大器配置是非反相放大器(图 2)。我总是想知道为什么我们不将其称为“常规放大器”配置,或者只是“放大器”。

同相放大器电路原理图。图 2同相放大器使用两个
电阻器为运算放大器提供负反馈。 在此配置中,我们看到有从输出到反相输入的反馈。这种负反馈意味着属性#4 被调用,并且两个输入之间的电压始终为零(即,它们处于相同的电压)。由于没有电流流入输入端,因此同相输入端的电压由 R 1和 R 2形成的分压器决定。

同相输入电压方程。

重新排列以获得放大器的增益,
获得放大器增益的方程。
请注意,电路的电压增益不取决于运算放大器的增益。我们假设如果运算放大器增益确实很大,那么足够的反馈将应用于非反相输入以产生所需的功能。
让我们检查一下关于两个运算放大器输入之间电压为零的假设。假设同相输入比反相输入高几毫伏。运算放大器的巨大电压增益会导致输出增加,这会通过电阻分压器反馈到反相输入。反相输入上的电压增加将导致运算放大器输出减小,直到两个输入具有相同的电压。因此,运算放大器的高增益加上负反馈使输入电压保持不变。
缓冲放大器 同相放大器的一种特殊情况是缓冲放大器(也称为单位增益放大器或电压跟随器),其电压增益为 1(图 3)。这相当于在同相放大器配置中使R 2为零且R 1无穷大。再次应用负反馈,使得运算放大器输入之间的电压为零。这构成了一个良好的缓冲放大器,输入端具有无限阻抗,输出端具有零阻抗。至少在理想情况下。

缓冲放大器电路原理图。图 3缓冲放大器提供无限输入阻抗和零输出阻抗。
反相放大器
另一种常见的运算放大器电路是反相放大器(图 4)。顾名思义,输出电压以与输入相反的极性进行放大。 反相放大器电路配置图。图 4反相放大器产生输入的负值,按两个电阻的比率缩放。

通过注意到运算放大器的两个输入均为 0V 来分析该电路。非反相输入接地,反相输入将通过电阻器的反馈被驱动到相同的电压。我们还注意到,电流 ( i ) 流过两个电阻,因为没有电流进入运算放大器的反相输入。

电流流过两个电阻的公式。
重新排列以获得放大器的增益,
反相放大器的增益公式。
增益中的负号很重要,在应用电路时必须予以考虑。在某些情况下,这可能并不重要,您可能只需要放大输入信号而不考虑极性的变化。在其他情况下,极性可能很关键,您的信号终可能会颠倒。
差分放大器
反相放大器和同相放大器可以组合起来形成差分放大器(也称为差分放大器),如图5所示。
差分放大器电路原理图。图 5差分放大器产生的输出电压是两个输入之间的差值。 应用叠加,我们可以组合反相和同相放大器配置的增益方程。

将 v 1替换为 v in,反相增益保持不变:
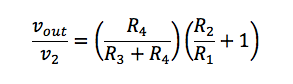
反相增益方程。 v 2输入具有一个由 R 3和 R 4组成的附加分压器,因此增益方程变为:

V2输入附加分压公式。 结合两个方程得出:

差分放大器方程。
如果我们设置 R 1 = R 3且 R 2 = R 4,则方程简化为:
设置电阻值方程。
我们假设我们有理想的运算放大器,但我们没有提及电阻器的任何内容。这些电路的增益将取决于电阻器的实际值及其容差。对于我们依赖匹配电阻值的差分放大器来说尤其如此。